Refereeing the Referees: Evaluating Two-Sample Tests for Validating Generators in Precision Sciences

We propose a robust methodology to evaluate the performance and computational efficiency of non-parametric two-sample tests, specifically designed for high-dimensional generative models in scientific applications such as in particle physics. The study focuses on tests built from univariate integral probability measures: the sliced Wasserstein distance and the mean of the Kolmogorov-Smirnov statistics, already discussed in the literature, and the novel sliced Kolmogorov-Smirnov statistic. These metrics can be evaluated in parallel, allowing for fast and reliable estimates of their distribution under the null hypothesis. We also compare these metrics with the recently proposed unbiased Fr\'echet Gaussian Distance and the unbiased quadratic Maximum Mean Discrepancy, computed with a quartic polynomial kernel. We evaluate the proposed tests on various distributions, focusing on their sensitivity to deformations parameterized by a single parameter $\epsilon$. Our experiments include correlated Gaussians and mixtures of Gaussians in 5, 20, and 100 dimensions, and a particle physics dataset of gluon jets from the JetNet dataset, considering both jet- and particle-level features. Our results demonstrate that one-dimensional-based tests provide a level of sensitivity comparable to other multivariate metrics, but with significantly lower computational cost, making them ideal for evaluating generative models in high-dimensional settings. This methodology offers an efficient, standardized tool for model comparison and can serve as a benchmark for more advanced tests, including machine-learning-based approaches.

The NFLikelihood: an unsupervised DNNLikelihood from Normalizing Flows

We propose the NFLikelihood, an unsupervised version, based on Normalizing Flows, of the DNNLikelihood proposed in Ref.[1]. We show, through realistic examples, how Autoregressive Flows, based on affine and rational quadratic spline bijectors, are able to learn complicated high-dimensional Likelihoods arising in High Energy Physics (HEP) analyses. We focus on a toy LHC analysis example already considered in the literature and on two Effective Field Theory fits of flavor and electroweak observables, whose samples have been obtained throught the HEPFit code. We discuss advantages and disadvantages of the unsupervised approach with respect to the supervised one and discuss possible interplays of the two.

On the curse of dimensionality for Normalizing Flows

Normalizing Flows have emerged as a powerful brand of generative models, as they not only allow for efficient sampling of complicated target distributions, but also deliver density estimation by construction. We propose here an in-depth comparison of coupling and autoregressive flows, both of the affine and rational quadratic spline type, considering four different architectures: Real-valued Non-Volume Preserving (RealNVP), Masked Autoregressive Flow (MAF), Coupling Rational Quadratic Spline (C-RQS), and Autoregressive Rational Quadratic Spline (A-RQS). We focus on different target distributions of increasing complexity with dimensionality ranging from 4 to 1000. The performances are discussed in terms of different figures of merit: the one-dimensional Wasserstein distance, the one-dimensional Kolmogorov-Smirnov test, the Frobenius norm of the difference between correlation matrices, and the training time. Our results indicate that the A-RQS algorithm stands out both in terms of accuracy and training speed. Nonetheless, all the algorithms are generally able, without much fine-tuning, to learn complex distributions with limited training data and in a reasonable time, of the order of hours on a Tesla V100 GPU. The only exception is the C-RQS, which takes significantly longer to train, and does not always provide good accuracy. All algorithms have been implemented using TensorFlow2 and TensorFlow Probability and made available on GitHub.

Testing the boundaries: Normalizing Flows for higher dimensional data sets

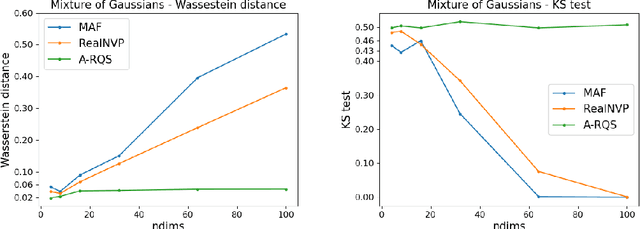
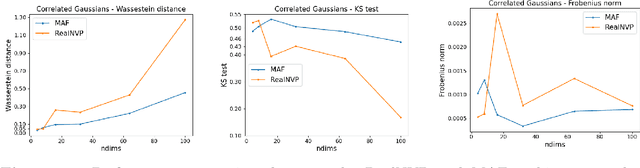
Normalizing Flows (NFs) are emerging as a powerful class of generative models, as they not only allow for efficient sampling, but also deliver, by construction, density estimation. They are of great potential usage in High Energy Physics (HEP), where complex high dimensional data and probability distributions are everyday's meal. However, in order to fully leverage the potential of NFs it is crucial to explore their robustness as data dimensionality increases. Thus, in this contribution, we discuss the performances of some of the most popular types of NFs on the market, on some toy data sets with increasing number of dimensions.