Automatic Gain Tuning for Humanoid Robots Walking Architectures Using Gradient-Free Optimization Techniques

Developing sophisticated control architectures has endowed robots, particularly humanoid robots, with numerous capabilities. However, tuning these architectures remains a challenging and time-consuming task that requires expert intervention. In this work, we propose a methodology to automatically tune the gains of all layers of a hierarchical control architecture for walking humanoids. We tested our methodology by employing different gradient-free optimization methods: Genetic Algorithm (GA), Covariance Matrix Adaptation Evolution Strategy (CMA-ES), Evolution Strategy (ES), and Differential Evolution (DE). We validated the parameter found both in simulation and on the real ergoCub humanoid robot. Our results show that GA achieves the fastest convergence (10 x 10^3 function evaluations vs 25 x 10^3 needed by the other algorithms) and 100% success rate in completing the task both in simulation and when transferred on the real robotic platform. These findings highlight the potential of our proposed method to automate the tuning process, reducing the need for manual intervention.

A New Formulation for Zeroth-Order Optimization of Adversarial EXEmples in Malware Detection

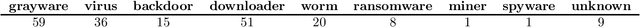
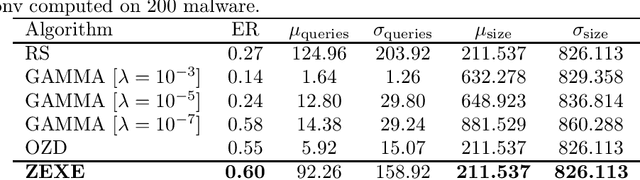
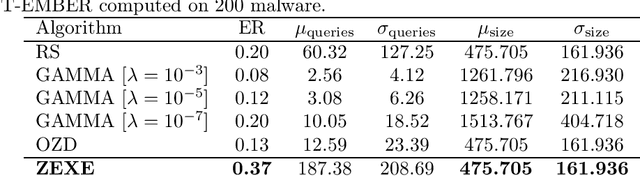
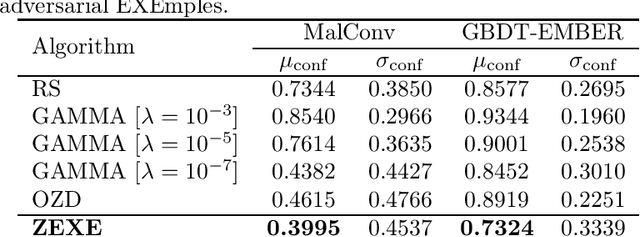
Machine learning malware detectors are vulnerable to adversarial EXEmples, i.e. carefully-crafted Windows programs tailored to evade detection. Unlike other adversarial problems, attacks in this context must be functionality-preserving, a constraint which is challenging to address. As a consequence heuristic algorithms are typically used, that inject new content, either randomly-picked or harvested from legitimate programs. In this paper, we show how learning malware detectors can be cast within a zeroth-order optimization framework which allows to incorporate functionality-preserving manipulations. This permits the deployment of sound and efficient gradient-free optimization algorithms, which come with theoretical guarantees and allow for minimal hyper-parameters tuning. As a by-product, we propose and study ZEXE, a novel zero-order attack against Windows malware detection. Compared to state-of-the-art techniques, ZEXE provides drastic improvement in the evasion rate, while reducing to less than one third the size of the injected content.

Q-Learning to navigate turbulence without a map

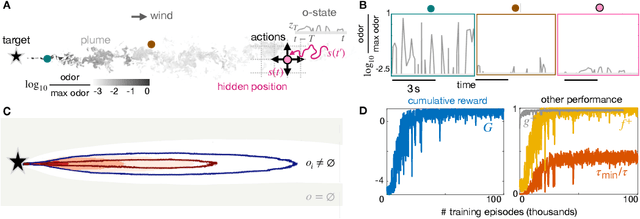
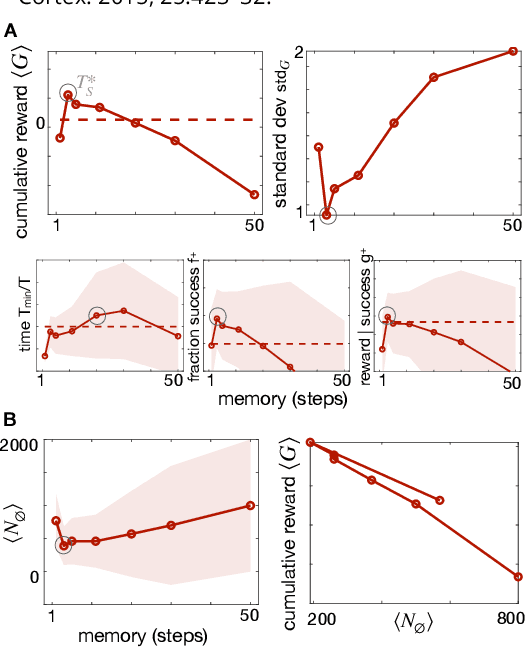
We consider the problem of olfactory searches in a turbulent environment. We focus on agents that respond solely to odor stimuli, with no access to spatial perception nor prior information about the odor location. We ask whether navigation strategies to a target can be learned robustly within a sequential decision making framework. We develop a reinforcement learning algorithm using a small set of interpretable olfactory states and train it with realistic turbulent odor cues. By introducing a temporal memory, we demonstrate that two salient features of odor traces, discretized in few olfactory states, are sufficient to learn navigation in a realistic odor plume. Performance is dictated by the sparse nature of turbulent plumes. An optimal memory exists which ignores blanks within the plume and activates a recovery strategy outside the plume. We obtain the best performance by letting agents learn their recovery strategy and show that it is mostly casting cross wind, similar to behavior observed in flying insects. The optimal strategy is robust to substantial changes in the odor plumes, suggesting minor parameter tuning may be sufficient to adapt to different environments.

Fast kernel methods for Data Quality Monitoring as a goodness-of-fit test

We here propose a machine learning approach for monitoring particle detectors in real-time. The goal is to assess the compatibility of incoming experimental data with a reference dataset, characterising the data behaviour under normal circumstances, via a likelihood-ratio hypothesis test. The model is based on a modern implementation of kernel methods, nonparametric algorithms that can learn any continuous function given enough data. The resulting approach is efficient and agnostic to the type of anomaly that may be present in the data. Our study demonstrates the effectiveness of this strategy on multivariate data from drift tube chamber muon detectors.

Efficient Unsupervised Learning for Plankton Images

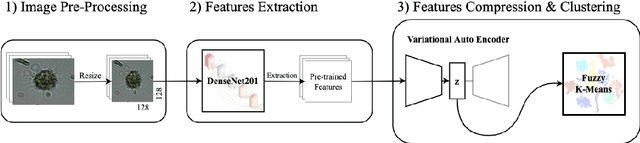
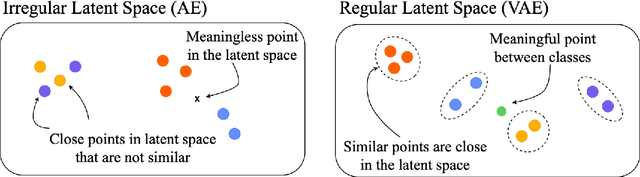
Monitoring plankton populations in situ is fundamental to preserve the aquatic ecosystem. Plankton microorganisms are in fact susceptible of minor environmental perturbations, that can reflect into consequent morphological and dynamical modifications. Nowadays, the availability of advanced automatic or semi-automatic acquisition systems has been allowing the production of an increasingly large amount of plankton image data. The adoption of machine learning algorithms to classify such data may be affected by the significant cost of manual annotation, due to both the huge quantity of acquired data and the numerosity of plankton species. To address these challenges, we propose an efficient unsupervised learning pipeline to provide accurate classification of plankton microorganisms. We build a set of image descriptors exploiting a two-step procedure. First, a Variational Autoencoder (VAE) is trained on features extracted by a pre-trained neural network. We then use the learnt latent space as image descriptor for clustering. We compare our method with state-of-the-art unsupervised approaches, where a set of pre-defined hand-crafted features is used for clustering of plankton images. The proposed pipeline outperforms the benchmark algorithms for all the plankton datasets included in our analysis, providing better image embedding properties.

Stochastic Zeroth order Descent with Structured Directions

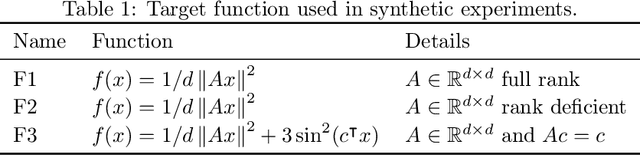
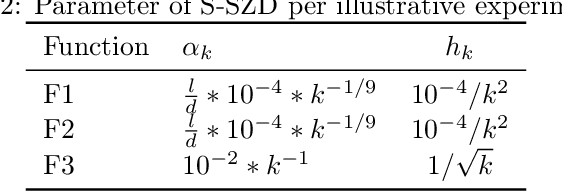
We introduce and analyze Structured Stochastic Zeroth order Descent (S-SZD), a finite difference approach which approximates a stochastic gradient on a set of $l\leq d$ orthogonal directions, where $d$ is the dimension of the ambient space. These directions are randomly chosen, and may change at each step. For smooth convex functions we prove almost sure convergence of the iterates and a convergence rate on the function values of the form $O(d/l k^{-c})$ for every $c<1/2$, which is arbitrarily close to the one of Stochastic Gradient Descent (SGD) in terms of number of iterations. Our bound also shows the benefits of using $l$ multiple directions instead of one. For non-convex functions satisfying the Polyak-{\L}ojasiewicz condition, we establish the first convergence rates for stochastic zeroth order algorithms under such an assumption. We corroborate our theoretical findings in numerical simulations where assumptions are satisfied and on the real-world problem of hyper-parameter optimization, observing that S-SZD has very good practical performances.

Learning new physics efficiently with nonparametric methods

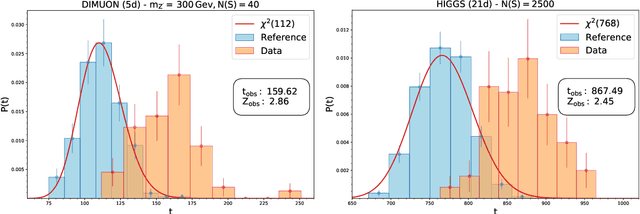
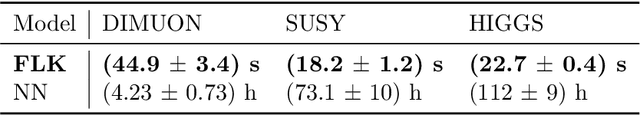
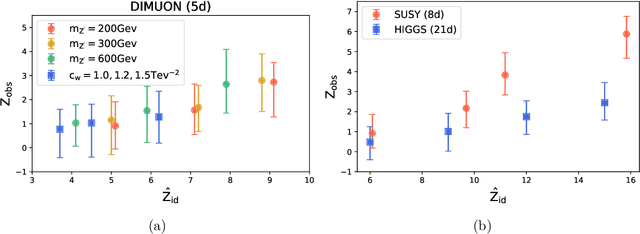
We present a machine learning approach for model-independent new physics searches. The corresponding algorithm is powered by recent large-scale implementations of kernel methods, nonparametric learning algorithms that can approximate any continuous function given enough data. Based on the original proposal by D'Agnolo and Wulzer (arXiv:1806.02350), the model evaluates the compatibility between experimental data and a reference model, by implementing a hypothesis testing procedure based on the likelihood ratio. Model-independence is enforced by avoiding any prior assumption about the presence or shape of new physics components in the measurements. We show that our approach has dramatic advantages compared to neural network implementations in terms of training times and computational resources, while maintaining comparable performances. In particular, we conduct our tests on higher dimensional datasets, a step forward with respect to previous studies.

Ada-BKB: Scalable Gaussian Process Optimization on Continuous Domain by Adaptive Discretization

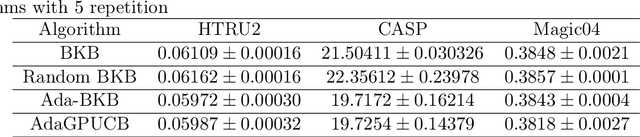
Gaussian process optimization is a successful class of algorithms (e.g. GP-UCB) to optimize a black-box function through sequential evaluations. However, when the domain of the function is continuous, Gaussian process optimization has to either rely on a fixed discretization of the space, or solve a non-convex optimization subproblem at each evaluation. The first approach can negatively affect performance, while the second one puts a heavy computational burden on the algorithm. A third option, that only recently has been theoretically studied, is to adaptively discretize the function domain. Even though this approach avoids the extra non-convex optimization costs, the overall computational complexity is still prohibitive. An algorithm such as GP-UCB has a runtime of $O(T^4)$, where $T$ is the number of iterations. In this paper, we introduce Ada-BKB (Adaptive Budgeted Kernelized Bandit), a no-regret Gaussian process optimization algorithm for functions on continuous domains, that provably runs in $O(T^2 d_\text{eff}^2)$, where $d_\text{eff}$ is the effective dimension of the explored space, and which is typically much smaller than $T$. We corroborate our findings with experiments on synthetic non-convex functions and on the real-world problem of hyper-parameter optimization.