Ada-BKB: Scalable Gaussian Process Optimization on Continuous Domain by Adaptive Discretization
Paper and Code
Jun 16, 2021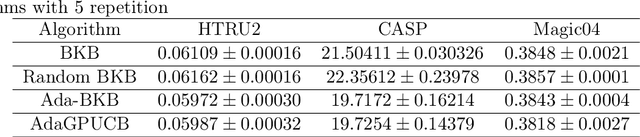



Gaussian process optimization is a successful class of algorithms (e.g. GP-UCB) to optimize a black-box function through sequential evaluations. However, when the domain of the function is continuous, Gaussian process optimization has to either rely on a fixed discretization of the space, or solve a non-convex optimization subproblem at each evaluation. The first approach can negatively affect performance, while the second one puts a heavy computational burden on the algorithm. A third option, that only recently has been theoretically studied, is to adaptively discretize the function domain. Even though this approach avoids the extra non-convex optimization costs, the overall computational complexity is still prohibitive. An algorithm such as GP-UCB has a runtime of $O(T^4)$, where $T$ is the number of iterations. In this paper, we introduce Ada-BKB (Adaptive Budgeted Kernelized Bandit), a no-regret Gaussian process optimization algorithm for functions on continuous domains, that provably runs in $O(T^2 d_\text{eff}^2)$, where $d_\text{eff}$ is the effective dimension of the explored space, and which is typically much smaller than $T$. We corroborate our findings with experiments on synthetic non-convex functions and on the real-world problem of hyper-parameter optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge