Scaling Gaussian Process Optimization by Evaluating a Few Unique Candidates Multiple Times

Computing a Gaussian process (GP) posterior has a computational cost cubical in the number of historical points. A reformulation of the same GP posterior highlights that this complexity mainly depends on how many \emph{unique} historical points are considered. This can have important implication in active learning settings, where the set of historical points is constructed sequentially by the learner. We show that sequential black-box optimization based on GPs (GP-Opt) can be made efficient by sticking to a candidate solution for multiple evaluation steps and switch only when necessary. Limiting the number of switches also limits the number of unique points in the history of the GP. Thus, the efficient GP reformulation can be used to exactly and cheaply compute the posteriors required to run the GP-Opt algorithms. This approach is especially useful in real-world applications of GP-Opt with high switch costs (e.g. switching chemicals in wet labs, data/model loading in hyperparameter optimization). As examples of this meta-approach, we modify two well-established GP-Opt algorithms, GP-UCB and GP-EI, to switch candidates as infrequently as possible adapting rules from batched GP-Opt. These versions preserve all the theoretical no-regret guarantees while improving practical aspects of the algorithms such as runtime, memory complexity, and the ability of batching candidates and evaluating them in parallel.

Efficient Hyperparameter Tuning for Large Scale Kernel Ridge Regression

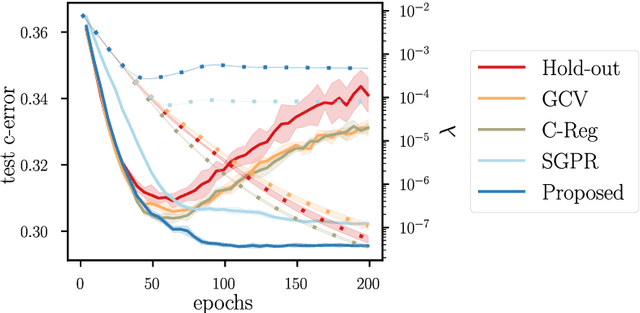
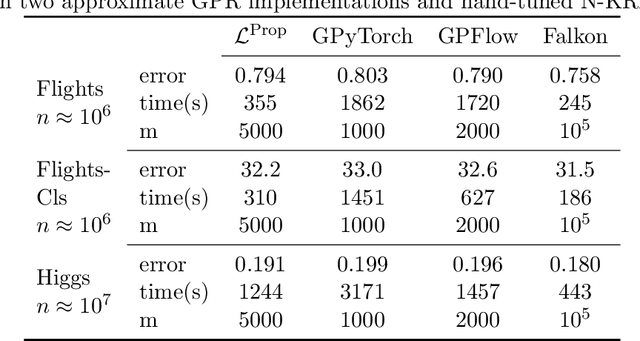
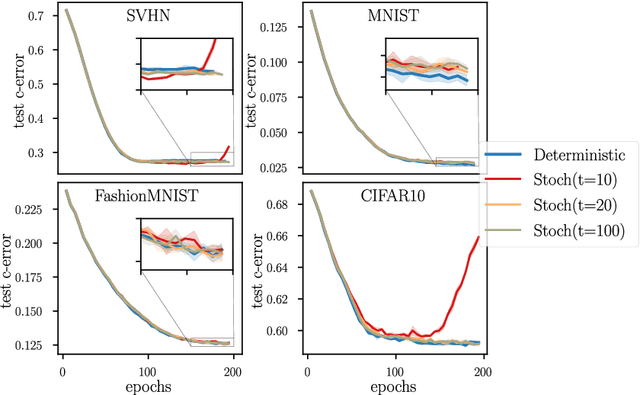
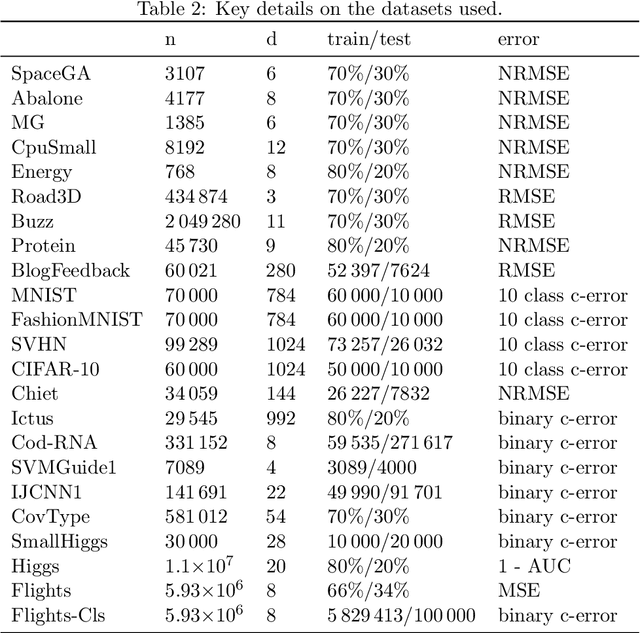
Kernel methods provide a principled approach to nonparametric learning. While their basic implementations scale poorly to large problems, recent advances showed that approximate solvers can efficiently handle massive datasets. A shortcoming of these solutions is that hyperparameter tuning is not taken care of, and left for the user to perform. Hyperparameters are crucial in practice and the lack of automated tuning greatly hinders efficiency and usability. In this paper, we work to fill in this gap focusing on kernel ridge regression based on the Nystr\"om approximation. After reviewing and contrasting a number of hyperparameter tuning strategies, we propose a complexity regularization criterion based on a data dependent penalty, and discuss its efficient optimization. Then, we proceed to a careful and extensive empirical evaluation highlighting strengths and weaknesses of the different tuning strategies. Our analysis shows the benefit of the proposed approach, that we hence incorporate in a library for large scale kernel methods to derive adaptively tuned solutions.

Mean Nyström Embeddings for Adaptive Compressive Learning

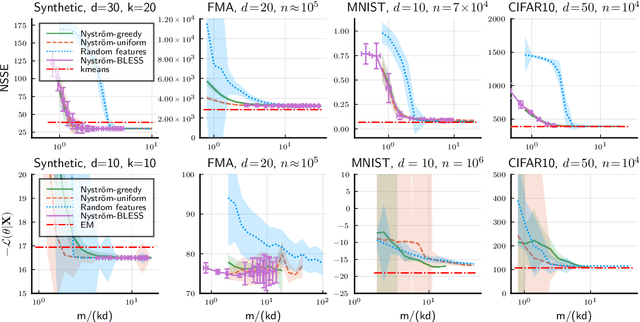
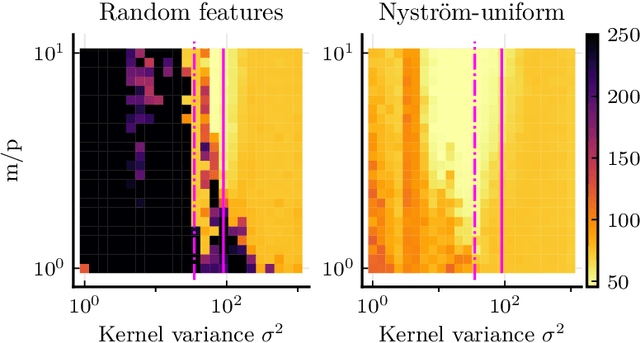
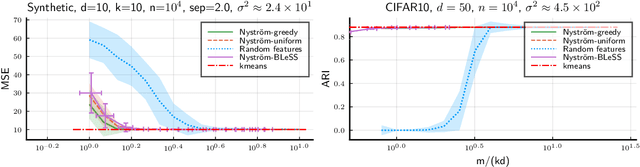
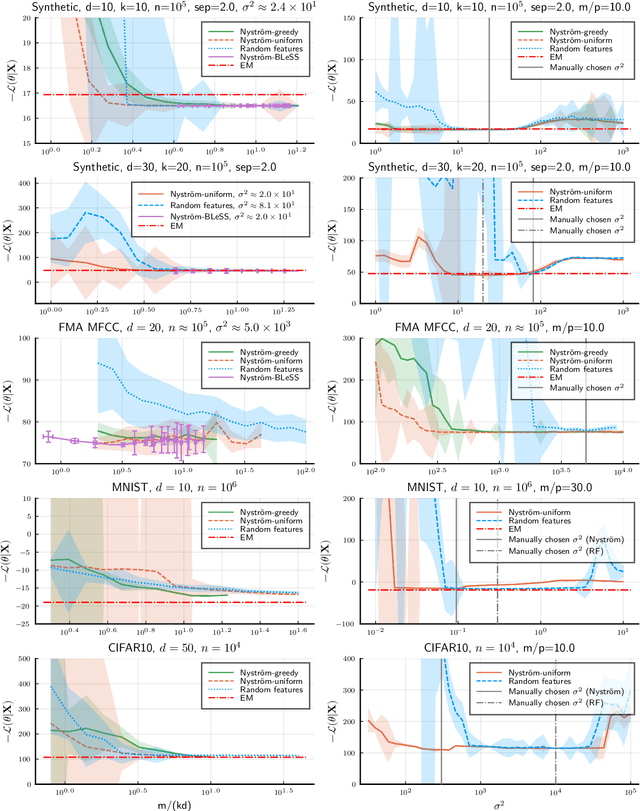
Compressive learning is an approach to efficient large scale learning based on sketching an entire dataset to a single mean embedding (the sketch), i.e. a vector of generalized moments. The learning task is then approximately solved as an inverse problem using an adapted parametric model. Previous works in this context have focused on sketches obtained by averaging random features, that while universal can be poorly adapted to the problem at hand. In this paper, we propose and study the idea of performing sketching based on data-dependent Nystr\"om approximation. From a theoretical perspective we prove that the excess risk can be controlled under a geometric assumption relating the parametric model used to learn from the sketch and the covariance operator associated to the task at hand. Empirically, we show for k-means clustering and Gaussian modeling that for a fixed sketch size, Nystr\"om sketches indeed outperform those built with random features.

ParK: Sound and Efficient Kernel Ridge Regression by Feature Space Partitions

We introduce ParK, a new large-scale solver for kernel ridge regression. Our approach combines partitioning with random projections and iterative optimization to reduce space and time complexity while provably maintaining the same statistical accuracy. In particular, constructing suitable partitions directly in the feature space rather than in the input space, we promote orthogonality between the local estimators, thus ensuring that key quantities such as local effective dimension and bias remain under control. We characterize the statistical-computational tradeoff of our model, and demonstrate the effectiveness of our method by numerical experiments on large-scale datasets.

Ada-BKB: Scalable Gaussian Process Optimization on Continuous Domain by Adaptive Discretization

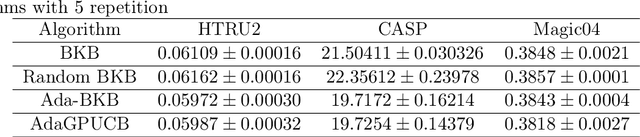
Gaussian process optimization is a successful class of algorithms (e.g. GP-UCB) to optimize a black-box function through sequential evaluations. However, when the domain of the function is continuous, Gaussian process optimization has to either rely on a fixed discretization of the space, or solve a non-convex optimization subproblem at each evaluation. The first approach can negatively affect performance, while the second one puts a heavy computational burden on the algorithm. A third option, that only recently has been theoretically studied, is to adaptively discretize the function domain. Even though this approach avoids the extra non-convex optimization costs, the overall computational complexity is still prohibitive. An algorithm such as GP-UCB has a runtime of $O(T^4)$, where $T$ is the number of iterations. In this paper, we introduce Ada-BKB (Adaptive Budgeted Kernelized Bandit), a no-regret Gaussian process optimization algorithm for functions on continuous domains, that provably runs in $O(T^2 d_\text{eff}^2)$, where $d_\text{eff}$ is the effective dimension of the explored space, and which is typically much smaller than $T$. We corroborate our findings with experiments on synthetic non-convex functions and on the real-world problem of hyper-parameter optimization.

Kernel methods through the roof: handling billions of points efficiently

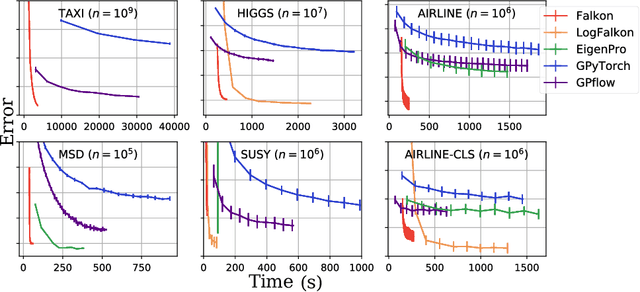
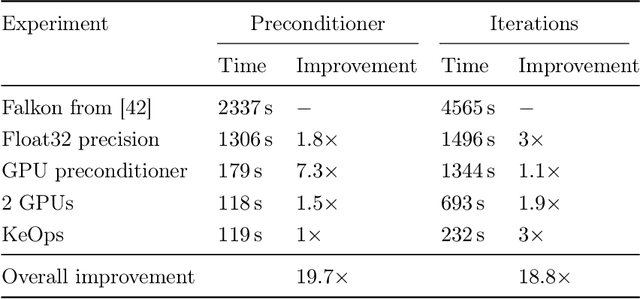
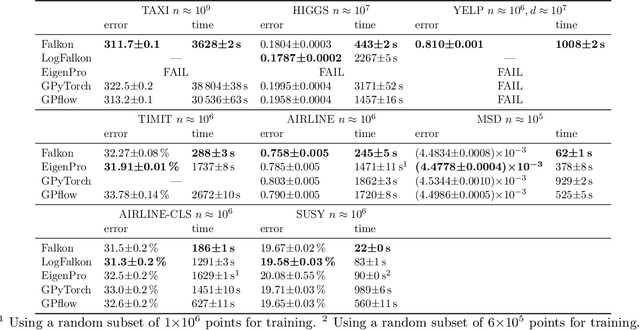
Kernel methods provide an elegant and principled approach to nonparametric learning, but so far could hardly be used in large scale problems, since na\"ive implementations scale poorly with data size. Recent advances have shown the benefits of a number of algorithmic ideas, for example combining optimization, numerical linear algebra and random projections. Here, we push these efforts further to develop and test a solver that takes full advantage of GPU hardware. Towards this end, we designed a preconditioned gradient solver for kernel methods exploiting both GPU acceleration and parallelization with multiple GPUs, implementing out-of-core variants of common linear algebra operations to guarantee optimal hardware utilization. Further, we optimize the numerical precision of different operations and maximize efficiency of matrix-vector multiplications. As a result we can experimentally show dramatic speedups on datasets with billions of points, while still guaranteeing state of the art performance. Additionally, we make our software available as an easy to use library.

On Mixup Regularization

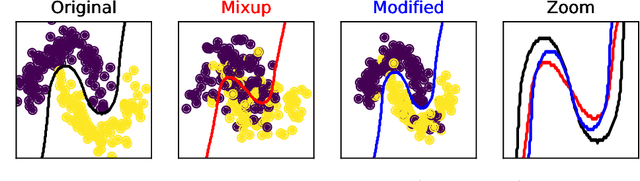
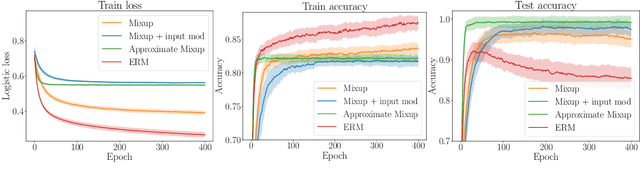
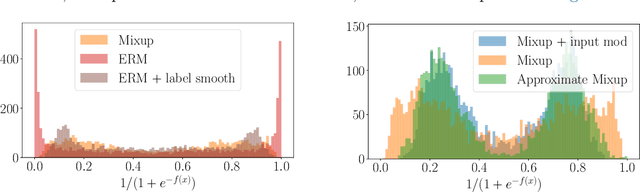
Mixup is a data augmentation technique that creates new examples as convex combinations of training points and labels. This simple technique has empirically shown to improve the accuracy of many state-of-the-art models in different settings and applications, but the reasons behind this empirical success remain poorly understood. In this paper we take a substantial step in explaining the theoretical foundations of Mixup, by clarifying its regularization effects. We show that Mixup can be interpreted as standard empirical risk minimization estimator subject to a combination of data transformation and random perturbation of the transformed data. We further show that these transformations and perturbations induce multiple known regularization schemes, including label smoothing and reduction of the Lipschitz constant of the estimator, and that these schemes interact synergistically with each other, resulting in a self calibrated and effective regularization effect that prevents overfitting and overconfident predictions. We illustrate our theoretical analysis by experiments that empirically support our conclusions.

Near-linear Time Gaussian Process Optimization with Adaptive Batching and Resparsification

Gaussian processes (GP) are one of the most successful frameworks to model uncertainty. However, GP optimization (e.g., GP-UCB) suffers from major scalability issues. Experimental time grows linearly with the number of evaluations, unless candidates are selected in batches (e.g., using GP-BUCB) and evaluated in parallel. Furthermore, computational cost is often prohibitive since algorithms such as GP-BUCB require a time at least quadratic in the number of dimensions and iterations to select each batch. In this paper, we introduce BBKB (Batch Budgeted Kernel Bandits), the first no-regret GP optimization algorithm that provably runs in near-linear time and selects candidates in batches. This is obtained with a new guarantee for the tracking of the posterior variances that allows BBKB to choose increasingly larger batches, improving over GP-BUCB. Moreover, we show that the same bound can be used to adaptively delay costly updates to the sparse GP approximation used by BBKB, achieving a near-constant per-step amortized cost. These findings are then confirmed in several experiments, where BBKB is much faster than state-of-the-art methods.

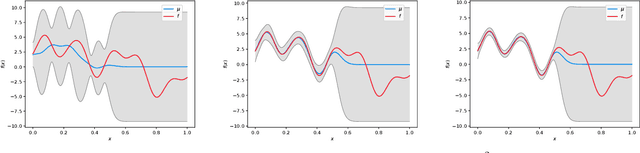
Gaussian Process Optimization with Adaptive Sketching: Scalable and No Regret

Gaussian processes (GP) are a popular Bayesian approach for the optimization of black-box functions. Despite their effectiveness in simple problems, GP-based algorithms hardly scale to complex high-dimensional functions, as their per-iteration time and space cost is at least quadratic in the number of dimensions $d$ and iterations $t$. Given a set of $A$ alternative to choose from, the overall runtime $O(t^3A)$ quickly becomes prohibitive. In this paper, we introduce BKB (budgeted kernelized bandit), a novel approximate GP algorithm for optimization under bandit feedback that achieves near-optimal regret (and hence near-optimal convergence rate) with near-constant per-iteration complexity and no assumption on the input space or covariance of the GP. Combining a kernelized linear bandit algorithm (GP-UCB) with randomized matrix sketching technique (i.e., leverage score sampling), we prove that selecting inducing points based on their posterior variance gives an accurate low-rank approximation of the GP, preserving variance estimates and confidence intervals. As a consequence, BKB does not suffer from variance starvation, an important problem faced by many previous sparse GP approximations. Moreover, we show that our procedure selects at most $\tilde{O}(d_{eff})$ points, where $d_{eff}$ is the effective dimension of the explored space, which is typically much smaller than both $d$ and $t$. This greatly reduces the dimensionality of the problem, thus leading to a $O(TAd_{eff}^2)$ runtime and $O(A d_{eff})$ space complexity.

Learning with SGD and Random Features

Sketching and stochastic gradient methods are arguably the most common techniques to derive efficient large scale learning algorithms. In this paper, we investigate their application in the context of nonparametric statistical learning. More precisely, we study the estimator defined by stochastic gradient with mini batches and random features. The latter can be seen as form of nonlinear sketching and used to define approximate kernel methods. The considered estimator is not explicitly penalized/constrained and regularization is implicit. Indeed, our study highlights how different parameters, such as number of features, iterations, step-size and mini-batch size control the learning properties of the solutions. We do this by deriving optimal finite sample bounds, under standard assumptions. The obtained results are corroborated and illustrated by numerical experiments.