CaloChallenge 2022: A Community Challenge for Fast Calorimeter Simulation

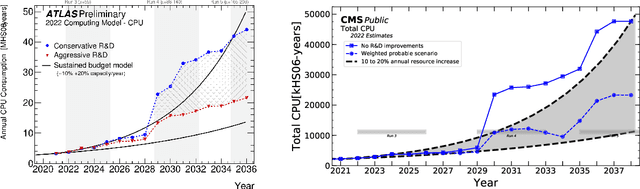
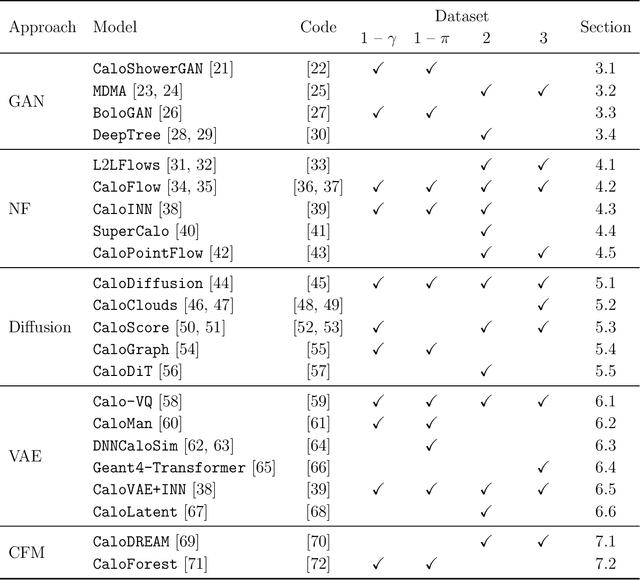
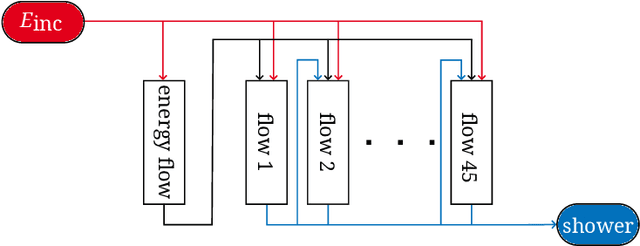
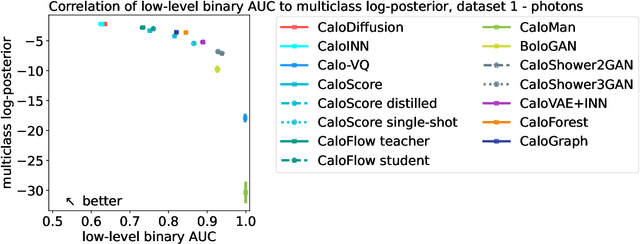
We present the results of the "Fast Calorimeter Simulation Challenge 2022" - the CaloChallenge. We study state-of-the-art generative models on four calorimeter shower datasets of increasing dimensionality, ranging from a few hundred voxels to a few tens of thousand voxels. The 31 individual submissions span a wide range of current popular generative architectures, including Variational AutoEncoders (VAEs), Generative Adversarial Networks (GANs), Normalizing Flows, Diffusion models, and models based on Conditional Flow Matching. We compare all submissions in terms of quality of generated calorimeter showers, as well as shower generation time and model size. To assess the quality we use a broad range of different metrics including differences in 1-dimensional histograms of observables, KPD/FPD scores, AUCs of binary classifiers, and the log-posterior of a multiclass classifier. The results of the CaloChallenge provide the most complete and comprehensive survey of cutting-edge approaches to calorimeter fast simulation to date. In addition, our work provides a uniquely detailed perspective on the important problem of how to evaluate generative models. As such, the results presented here should be applicable for other domains that use generative AI and require fast and faithful generation of samples in a large phase space.

TabDPT: Scaling Tabular Foundation Models

The challenges faced by neural networks on tabular data are well-documented and have hampered the progress of tabular foundation models. Techniques leveraging in-context learning (ICL) have shown promise here, allowing for dynamic adaptation to unseen data. ICL can provide predictions for entirely new datasets without further training or hyperparameter tuning, therefore providing very fast inference when encountering a novel task. However, scaling ICL for tabular data remains an issue: approaches based on large language models cannot efficiently process numeric tables, and tabular-specific techniques have not been able to effectively harness the power of real data to improve performance and generalization. We are able to overcome these challenges by training tabular-specific ICL-based architectures on real data with self-supervised learning and retrieval, combining the best of both worlds. Our resulting model -- the Tabular Discriminative Pre-trained Transformer (TabDPT) -- achieves state-of-the-art performance on the CC18 (classification) and CTR23 (regression) benchmarks with no task-specific fine-tuning, demonstrating the adapatability and speed of ICL once the model is pre-trained. TabDPT also demonstrates strong scaling as both model size and amount of available data increase, pointing towards future improvements simply through the curation of larger tabular pre-training datasets and training larger models.

Deep Generative Models through the Lens of the Manifold Hypothesis: A Survey and New Connections

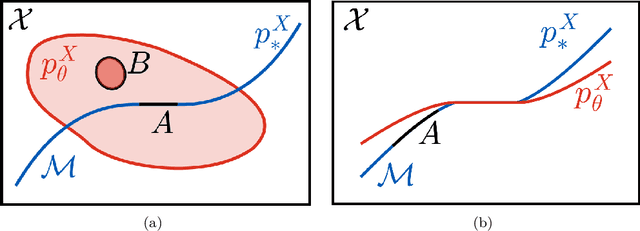
In recent years there has been increased interest in understanding the interplay between deep generative models (DGMs) and the manifold hypothesis. Research in this area focuses on understanding the reasons why commonly-used DGMs succeed or fail at learning distributions supported on unknown low-dimensional manifolds, as well as developing new models explicitly designed to account for manifold-supported data. This manifold lens provides both clarity as to why some DGMs (e.g. diffusion models and some generative adversarial networks) empirically surpass others (e.g. likelihood-based models such as variational autoencoders, normalizing flows, or energy-based models) at sample generation, and guidance for devising more performant DGMs. We carry out the first survey of DGMs viewed through this lens, making two novel contributions along the way. First, we formally establish that numerical instability of high-dimensional likelihoods is unavoidable when modelling low-dimensional data. We then show that DGMs on learned representations of autoencoders can be interpreted as approximately minimizing Wasserstein distance: this result, which applies to latent diffusion models, helps justify their outstanding empirical results. The manifold lens provides a rich perspective from which to understand DGMs, which we aim to make more accessible and widespread.

A Geometric Explanation of the Likelihood OOD Detection Paradox

Likelihood-based deep generative models (DGMs) commonly exhibit a puzzling behaviour: when trained on a relatively complex dataset, they assign higher likelihood values to out-of-distribution (OOD) data from simpler sources. Adding to the mystery, OOD samples are never generated by these DGMs despite having higher likelihoods. This two-pronged paradox has yet to be conclusively explained, making likelihood-based OOD detection unreliable. Our primary observation is that high-likelihood regions will not be generated if they contain minimal probability mass. We demonstrate how this seeming contradiction of large densities yet low probability mass can occur around data confined to low-dimensional manifolds. We also show that this scenario can be identified through local intrinsic dimension (LID) estimation, and propose a method for OOD detection which pairs the likelihoods and LID estimates obtained from a pre-trained DGM. Our method can be applied to normalizing flows and score-based diffusion models, and obtains results which match or surpass state-of-the-art OOD detection benchmarks using the same DGM backbones. Our code is available at https://github.com/layer6ai-labs/dgm_ood_detection.

Exposing flaws of generative model evaluation metrics and their unfair treatment of diffusion models

We systematically study a wide variety of image-based generative models spanning semantically-diverse datasets to understand and improve the feature extractors and metrics used to evaluate them. Using best practices in psychophysics, we measure human perception of image realism for generated samples by conducting the largest experiment evaluating generative models to date, and find that no existing metric strongly correlates with human evaluations. Comparing to 16 modern metrics for evaluating the overall performance, fidelity, diversity, and memorization of generative models, we find that the state-of-the-art perceptual realism of diffusion models as judged by humans is not reflected in commonly reported metrics such as FID. This discrepancy is not explained by diversity in generated samples, though one cause is over-reliance on Inception-V3. We address these flaws through a study of alternative self-supervised feature extractors, find that the semantic information encoded by individual networks strongly depends on their training procedure, and show that DINOv2-ViT-L/14 allows for much richer evaluation of generative models. Next, we investigate data memorization, and find that generative models do memorize training examples on simple, smaller datasets like CIFAR10, but not necessarily on more complex datasets like ImageNet. However, our experiments show that current metrics do not properly detect memorization; none in the literature is able to separate memorization from other phenomena such as underfitting or mode shrinkage. To facilitate further development of generative models and their evaluation we release all generated image datasets, human evaluation data, and a modular library to compute 16 common metrics for 8 different encoders at https://github.com/layer6ai-labs/dgm-eval.

Denoising Deep Generative Models

Likelihood-based deep generative models have recently been shown to exhibit pathological behaviour under the manifold hypothesis as a consequence of using high-dimensional densities to model data with low-dimensional structure. In this paper we propose two methodologies aimed at addressing this problem. Both are based on adding Gaussian noise to the data to remove the dimensionality mismatch during training, and both provide a denoising mechanism whose goal is to sample from the model as though no noise had been added to the data. Our first approach is based on Tweedie's formula, and the second on models which take the variance of added noise as a conditional input. We show that surprisingly, while well motivated, these approaches only sporadically improve performance over not adding noise, and that other methods of addressing the dimensionality mismatch are more empirically adequate.

CaloMan: Fast generation of calorimeter showers with density estimation on learned manifolds

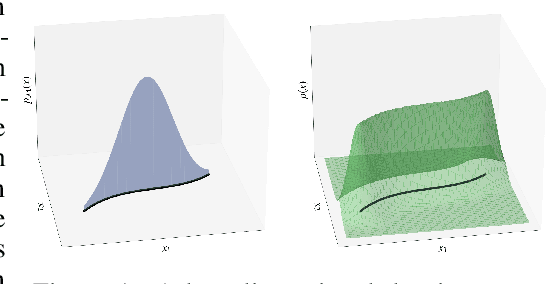
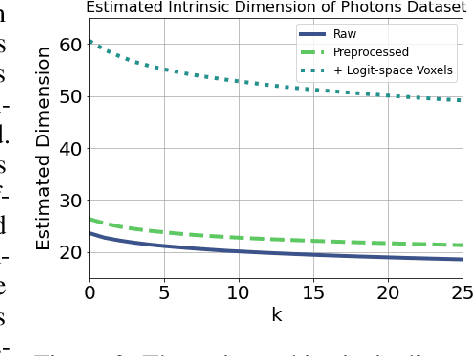
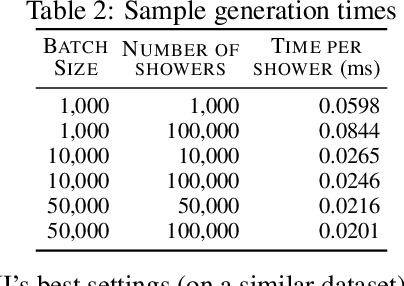
Precision measurements and new physics searches at the Large Hadron Collider require efficient simulations of particle propagation and interactions within the detectors. The most computationally expensive simulations involve calorimeter showers. Advances in deep generative modelling - particularly in the realm of high-dimensional data - have opened the possibility of generating realistic calorimeter showers orders of magnitude more quickly than physics-based simulation. However, the high-dimensional representation of showers belies the relative simplicity and structure of the underlying physical laws. This phenomenon is yet another example of the manifold hypothesis from machine learning, which states that high-dimensional data is supported on low-dimensional manifolds. We thus propose modelling calorimeter showers first by learning their manifold structure, and then estimating the density of data across this manifold. Learning manifold structure reduces the dimensionality of the data, which enables fast training and generation when compared with competing methods.

Relating Regularization and Generalization through the Intrinsic Dimension of Activations

Given a pair of models with similar training set performance, it is natural to assume that the model that possesses simpler internal representations would exhibit better generalization. In this work, we provide empirical evidence for this intuition through an analysis of the intrinsic dimension (ID) of model activations, which can be thought of as the minimal number of factors of variation in the model's representation of the data. First, we show that common regularization techniques uniformly decrease the last-layer ID (LLID) of validation set activations for image classification models and show how this strongly affects generalization performance. We also investigate how excessive regularization decreases a model's ability to extract features from data in earlier layers, leading to a negative effect on validation accuracy even while LLID continues to decrease and training accuracy remains near-perfect. Finally, we examine the LLID over the course of training of models that exhibit grokking. We observe that well after training accuracy saturates, when models ``grok'' and validation accuracy suddenly improves from random to perfect, there is a co-occurent sudden drop in LLID, thus providing more insight into the dynamics of sudden generalization.

The Union of Manifolds Hypothesis and its Implications for Deep Generative Modelling

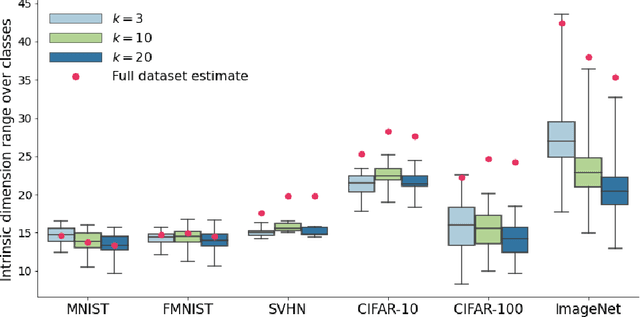
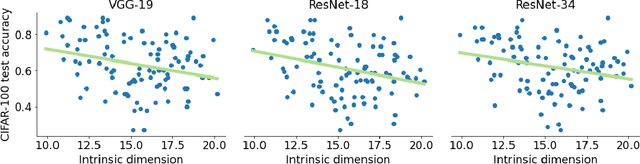
Deep learning has had tremendous success at learning low-dimensional representations of high-dimensional data. This success would be impossible if there was no hidden low-dimensional structure in data of interest; this existence is posited by the manifold hypothesis, which states that the data lies on an unknown manifold of low intrinsic dimension. In this paper, we argue that this hypothesis does not properly capture the low-dimensional structure typically present in data. Assuming the data lies on a single manifold implies intrinsic dimension is identical across the entire data space, and does not allow for subregions of this space to have a different number of factors of variation. To address this deficiency, we put forth the union of manifolds hypothesis, which accommodates the existence of non-constant intrinsic dimensions. We empirically verify this hypothesis on commonly-used image datasets, finding that indeed, intrinsic dimension should be allowed to vary. We also show that classes with higher intrinsic dimensions are harder to classify, and how this insight can be used to improve classification accuracy. We then turn our attention to the impact of this hypothesis in the context of deep generative models (DGMs). Most current DGMs struggle to model datasets with several connected components and/or varying intrinsic dimensions. To tackle these shortcomings, we propose clustered DGMs, where we first cluster the data and then train a DGM on each cluster. We show that clustered DGMs can model multiple connected components with different intrinsic dimensions, and empirically outperform their non-clustered counterparts without increasing computational requirements.

Neural Implicit Manifold Learning for Topology-Aware Generative Modelling

Natural data observed in $\mathbb{R}^n$ is often constrained to an $m$-dimensional manifold $\mathcal{M}$, where $m < n$. Current generative models represent this manifold by mapping an $m$-dimensional latent variable through a neural network $f_\theta: \mathbb{R}^m \to \mathbb{R}^n$. Such procedures, which we call pushforward models, incur a straightforward limitation: manifolds cannot in general be represented with a single parameterization, meaning that attempts to do so will incur either computational instability or the inability to learn probability densities within the manifold. To remedy this problem, we propose to model $\mathcal{M}$ as a neural implicit manifold: the set of zeros of a neural network. To learn the data distribution within $\mathcal{M}$, we introduce constrained energy-based models, which use a constrained variant of Langevin dynamics to train and sample within the learned manifold. The resulting model can be manipulated with an arithmetic of manifolds which allows practitioners to take unions and intersections of model manifolds. In experiments on synthetic and natural data, we show that constrained EBMs can learn manifold-supported distributions with complex topologies more accurately than pushforward models.