The Union of Manifolds Hypothesis and its Implications for Deep Generative Modelling

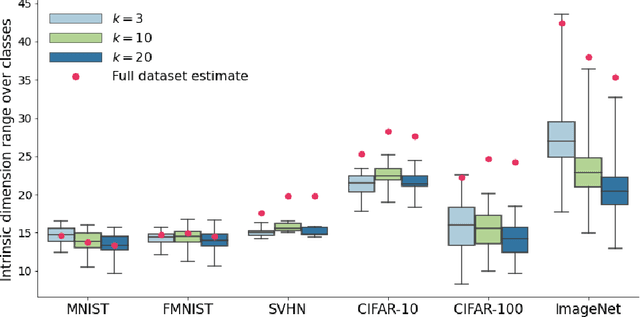
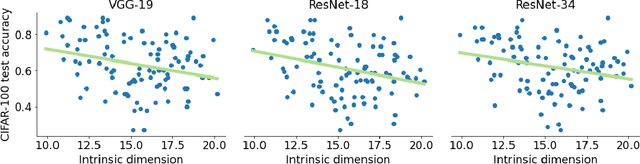
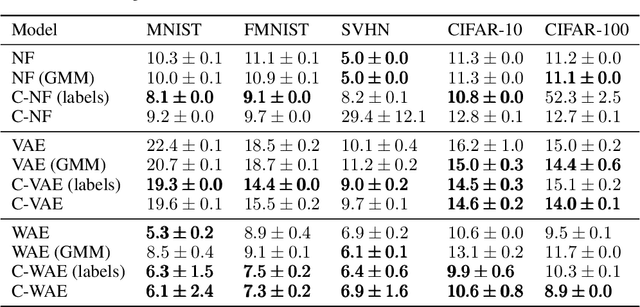
Deep learning has had tremendous success at learning low-dimensional representations of high-dimensional data. This success would be impossible if there was no hidden low-dimensional structure in data of interest; this existence is posited by the manifold hypothesis, which states that the data lies on an unknown manifold of low intrinsic dimension. In this paper, we argue that this hypothesis does not properly capture the low-dimensional structure typically present in data. Assuming the data lies on a single manifold implies intrinsic dimension is identical across the entire data space, and does not allow for subregions of this space to have a different number of factors of variation. To address this deficiency, we put forth the union of manifolds hypothesis, which accommodates the existence of non-constant intrinsic dimensions. We empirically verify this hypothesis on commonly-used image datasets, finding that indeed, intrinsic dimension should be allowed to vary. We also show that classes with higher intrinsic dimensions are harder to classify, and how this insight can be used to improve classification accuracy. We then turn our attention to the impact of this hypothesis in the context of deep generative models (DGMs). Most current DGMs struggle to model datasets with several connected components and/or varying intrinsic dimensions. To tackle these shortcomings, we propose clustered DGMs, where we first cluster the data and then train a DGM on each cluster. We show that clustered DGMs can model multiple connected components with different intrinsic dimensions, and empirically outperform their non-clustered counterparts without increasing computational requirements.