A Geometric Framework for Understanding Memorization in Generative Models

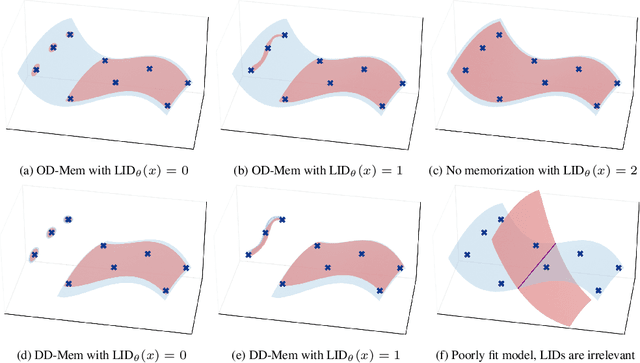
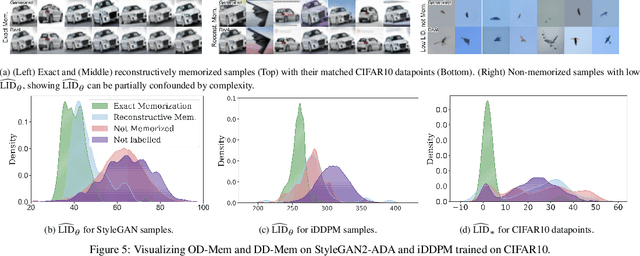
As deep generative models have progressed, recent work has shown them to be capable of memorizing and reproducing training datapoints when deployed. These findings call into question the usability of generative models, especially in light of the legal and privacy risks brought about by memorization. To better understand this phenomenon, we propose the manifold memorization hypothesis (MMH), a geometric framework which leverages the manifold hypothesis into a clear language in which to reason about memorization. We propose to analyze memorization in terms of the relationship between the dimensionalities of $(i)$ the ground truth data manifold and $(ii)$ the manifold learned by the model. This framework provides a formal standard for "how memorized" a datapoint is and systematically categorizes memorized data into two types: memorization driven by overfitting and memorization driven by the underlying data distribution. By analyzing prior work in the context of the MMH, we explain and unify assorted observations in the literature. We empirically validate the MMH using synthetic data and image datasets up to the scale of Stable Diffusion, developing new tools for detecting and preventing generation of memorized samples in the process.

TabDPT: Scaling Tabular Foundation Models

The challenges faced by neural networks on tabular data are well-documented and have hampered the progress of tabular foundation models. Techniques leveraging in-context learning (ICL) have shown promise here, allowing for dynamic adaptation to unseen data. ICL can provide predictions for entirely new datasets without further training or hyperparameter tuning, therefore providing very fast inference when encountering a novel task. However, scaling ICL for tabular data remains an issue: approaches based on large language models cannot efficiently process numeric tables, and tabular-specific techniques have not been able to effectively harness the power of real data to improve performance and generalization. We are able to overcome these challenges by training tabular-specific ICL-based architectures on real data with self-supervised learning and retrieval, combining the best of both worlds. Our resulting model -- the Tabular Discriminative Pre-trained Transformer (TabDPT) -- achieves state-of-the-art performance on the CC18 (classification) and CTR23 (regression) benchmarks with no task-specific fine-tuning, demonstrating the adapatability and speed of ICL once the model is pre-trained. TabDPT also demonstrates strong scaling as both model size and amount of available data increase, pointing towards future improvements simply through the curation of larger tabular pre-training datasets and training larger models.

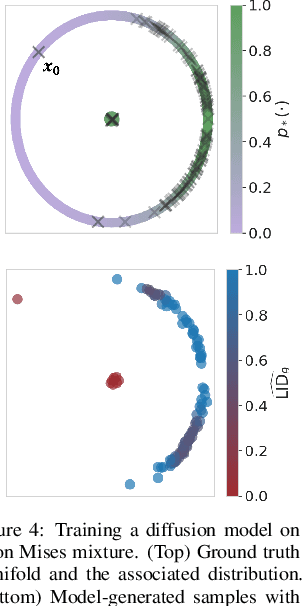
A Geometric View of Data Complexity: Efficient Local Intrinsic Dimension Estimation with Diffusion Models

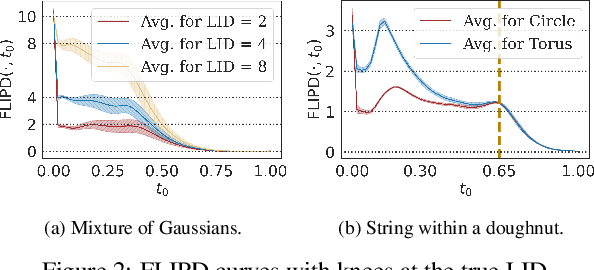
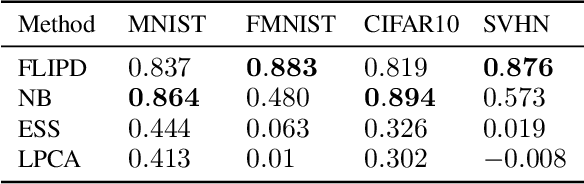
High-dimensional data commonly lies on low-dimensional submanifolds, and estimating the local intrinsic dimension (LID) of a datum -- i.e. the dimension of the submanifold it belongs to -- is a longstanding problem. LID can be understood as the number of local factors of variation: the more factors of variation a datum has, the more complex it tends to be. Estimating this quantity has proven useful in contexts ranging from generalization in neural networks to detection of out-of-distribution data, adversarial examples, and AI-generated text. The recent successes of deep generative models present an opportunity to leverage them for LID estimation, but current methods based on generative models produce inaccurate estimates, require more than a single pre-trained model, are computationally intensive, or do not exploit the best available deep generative models, i.e. diffusion models (DMs). In this work, we show that the Fokker-Planck equation associated with a DM can provide a LID estimator which addresses all the aforementioned deficiencies. Our estimator, called FLIPD, is compatible with all popular DMs, and outperforms existing baselines on LID estimation benchmarks. We also apply FLIPD on natural images where the true LID is unknown. Compared to competing estimators, FLIPD exhibits a higher correlation with non-LID measures of complexity, better matches a qualitative assessment of complexity, and is the only estimator to remain tractable with high-resolution images at the scale of Stable Diffusion.

A Geometric Explanation of the Likelihood OOD Detection Paradox

Likelihood-based deep generative models (DGMs) commonly exhibit a puzzling behaviour: when trained on a relatively complex dataset, they assign higher likelihood values to out-of-distribution (OOD) data from simpler sources. Adding to the mystery, OOD samples are never generated by these DGMs despite having higher likelihoods. This two-pronged paradox has yet to be conclusively explained, making likelihood-based OOD detection unreliable. Our primary observation is that high-likelihood regions will not be generated if they contain minimal probability mass. We demonstrate how this seeming contradiction of large densities yet low probability mass can occur around data confined to low-dimensional manifolds. We also show that this scenario can be identified through local intrinsic dimension (LID) estimation, and propose a method for OOD detection which pairs the likelihoods and LID estimates obtained from a pre-trained DGM. Our method can be applied to normalizing flows and score-based diffusion models, and obtains results which match or surpass state-of-the-art OOD detection benchmarks using the same DGM backbones. Our code is available at https://github.com/layer6ai-labs/dgm_ood_detection.

OCDaf: Ordered Causal Discovery with Autoregressive Flows

We propose OCDaf, a novel order-based method for learning causal graphs from observational data. We establish the identifiability of causal graphs within multivariate heteroscedastic noise models, a generalization of additive noise models that allow for non-constant noise variances. Drawing upon the structural similarities between these models and affine autoregressive normalizing flows, we introduce a continuous search algorithm to find causal structures. Our experiments demonstrate state-of-the-art performance across the Sachs and SynTReN benchmarks in Structural Hamming Distance (SHD) and Structural Intervention Distance (SID). Furthermore, we validate our identifiability theory across various parametric and nonparametric synthetic datasets and showcase superior performance compared to existing baselines.