Applications of Statistical Field Theory in Deep Learning

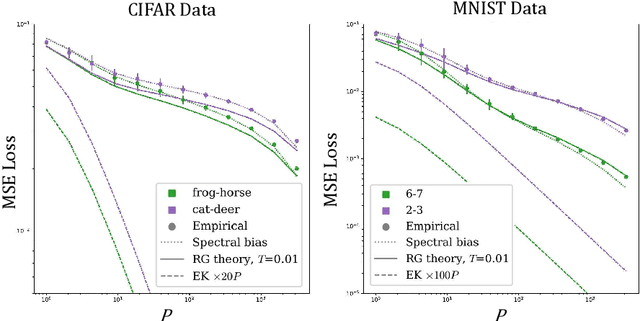
Deep learning algorithms have made incredible strides in the past decade yet due to the complexity of these algorithms, the science of deep learning remains in its early stages. Being an experimentally driven field, it is natural to seek a theory of deep learning within the physics paradigm. As deep learning is largely about learning functions and distributions over functions, statistical field theory, a rich and versatile toolbox for tackling complex distributions over functions (fields) is an obvious choice of formalism. Research efforts carried out in the past few years have demonstrated the ability of field theory to provide useful insights on generalization, implicit bias, and feature learning effects. Here we provide a pedagogical review of this emerging line of research.

From Kernels to Features: A Multi-Scale Adaptive Theory of Feature Learning

Theoretically describing feature learning in neural networks is crucial for understanding their expressive power and inductive biases, motivating various approaches. Some approaches describe network behavior after training through a simple change in kernel scale from initialization, resulting in a generalization power comparable to a Gaussian process. Conversely, in other approaches training results in the adaptation of the kernel to the data, involving complex directional changes to the kernel. While these approaches capture different facets of network behavior, their relationship and respective strengths across scaling regimes remains an open question. This work presents a theoretical framework of multi-scale adaptive feature learning bridging these approaches. Using methods from statistical mechanics, we derive analytical expressions for network output statistics which are valid across scaling regimes and in the continuum between them. A systematic expansion of the network's probability distribution reveals that mean-field scaling requires only a saddle-point approximation, while standard scaling necessitates additional correction terms. Remarkably, we find across regimes that kernel adaptation can be reduced to an effective kernel rescaling when predicting the mean network output of a linear network. However, even in this case, the multi-scale adaptive approach captures directional feature learning effects, providing richer insights than what could be recovered from a rescaling of the kernel alone.

Graph Neural Networks Do Not Always Oversmooth

Graph neural networks (GNNs) have emerged as powerful tools for processing relational data in applications. However, GNNs suffer from the problem of oversmoothing, the property that the features of all nodes exponentially converge to the same vector over layers, prohibiting the design of deep GNNs. In this work we study oversmoothing in graph convolutional networks (GCNs) by using their Gaussian process (GP) equivalence in the limit of infinitely many hidden features. By generalizing methods from conventional deep neural networks (DNNs), we can describe the distribution of features at the output layer of deep GCNs in terms of a GP: as expected, we find that typical parameter choices from the literature lead to oversmoothing. The theory, however, allows us to identify a new, nonoversmoothing phase: if the initial weights of the network have sufficiently large variance, GCNs do not oversmooth, and node features remain informative even at large depth. We demonstrate the validity of this prediction in finite-size GCNs by training a linear classifier on their output. Moreover, using the linearization of the GCN GP, we generalize the concept of propagation depth of information from DNNs to GCNs. This propagation depth diverges at the transition between the oversmoothing and non-oversmoothing phase. We test the predictions of our approach and find good agreement with finite-size GCNs. Initializing GCNs near the transition to the non-oversmoothing phase, we obtain networks which are both deep and expressive.

A theory of data variability in Neural Network Bayesian inference

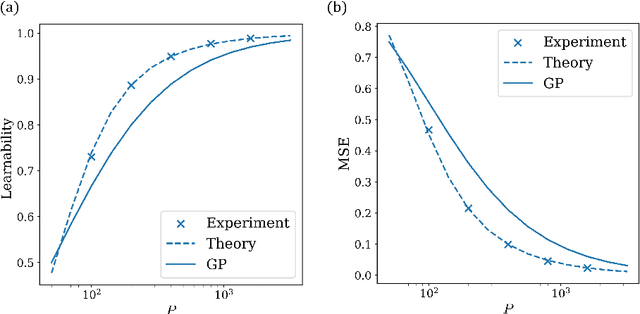
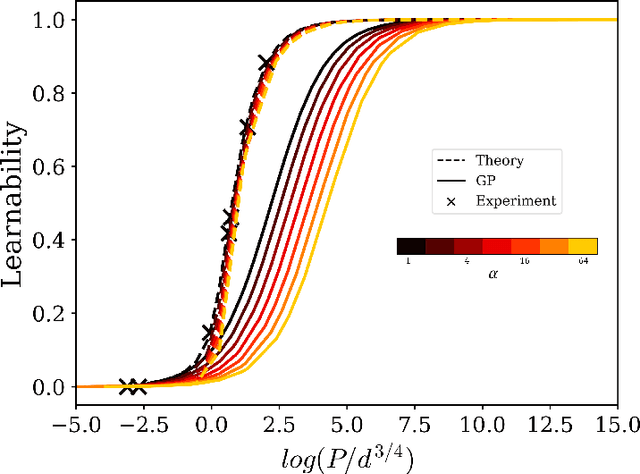
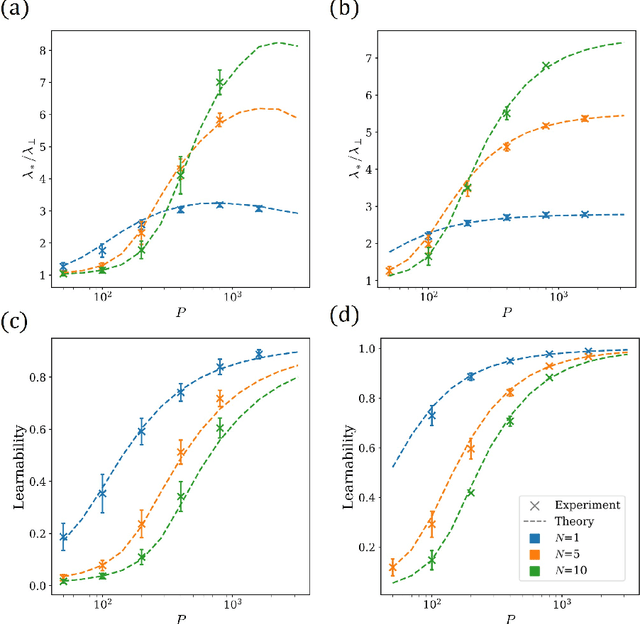
Bayesian inference and kernel methods are well established in machine learning. The neural network Gaussian process in particular provides a concept to investigate neural networks in the limit of infinitely wide hidden layers by using kernel and inference methods. Here we build upon this limit and provide a field-theoretic formalism which covers the generalization properties of infinitely wide networks. We systematically compute generalization properties of linear, non-linear, and deep non-linear networks for kernel matrices with heterogeneous entries. In contrast to currently employed spectral methods we derive the generalization properties from the statistical properties of the input, elucidating the interplay of input dimensionality, size of the training data set, and variability of the data. We show that data variability leads to a non-Gaussian action reminiscent of a ($\varphi^3+\varphi^4$)-theory. Using our formalism on a synthetic task and on MNIST we obtain a homogeneous kernel matrix approximation for the learning curve as well as corrections due to data variability which allow the estimation of the generalization properties and exact results for the bounds of the learning curves in the case of infinitely many training data points.

Speed Limits for Deep Learning

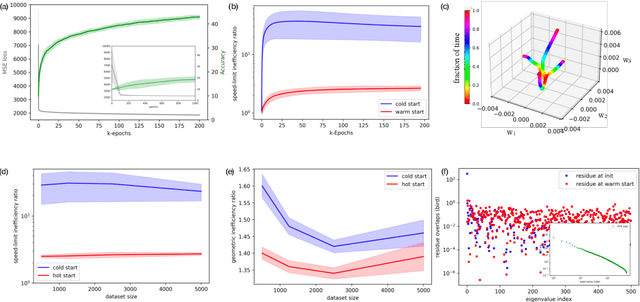
State-of-the-art neural networks require extreme computational power to train. It is therefore natural to wonder whether they are optimally trained. Here we apply a recent advancement in stochastic thermodynamics which allows bounding the speed at which one can go from the initial weight distribution to the final distribution of the fully trained network, based on the ratio of their Wasserstein-2 distance and the entropy production rate of the dynamical process connecting them. Considering both gradient-flow and Langevin training dynamics, we provide analytical expressions for these speed limits for linear and linearizable neural networks e.g. Neural Tangent Kernel (NTK). Remarkably, given some plausible scaling assumptions on the NTK spectra and spectral decomposition of the labels -- learning is optimal in a scaling sense. Our results are consistent with small-scale experiments with Convolutional Neural Networks (CNNs) and Fully Connected Neural networks (FCNs) on CIFAR-10, showing a short highly non-optimal regime followed by a longer optimal regime.

Optimal signal propagation in ResNets through residual scaling

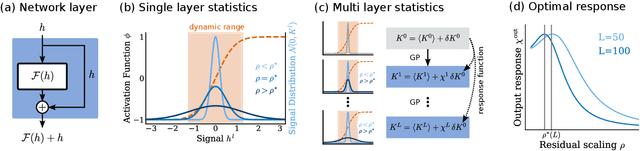
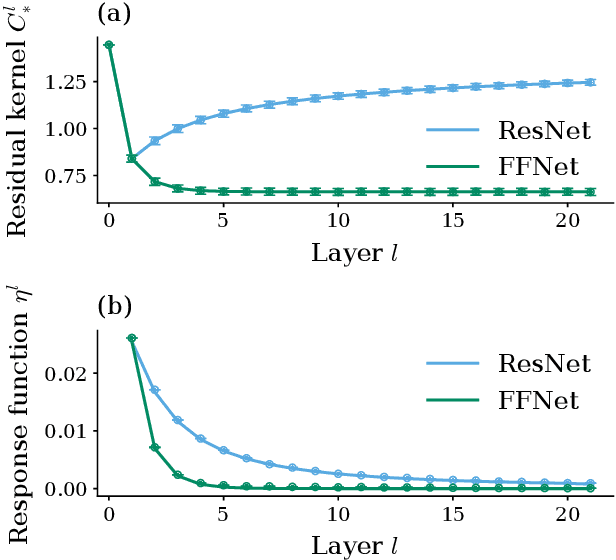
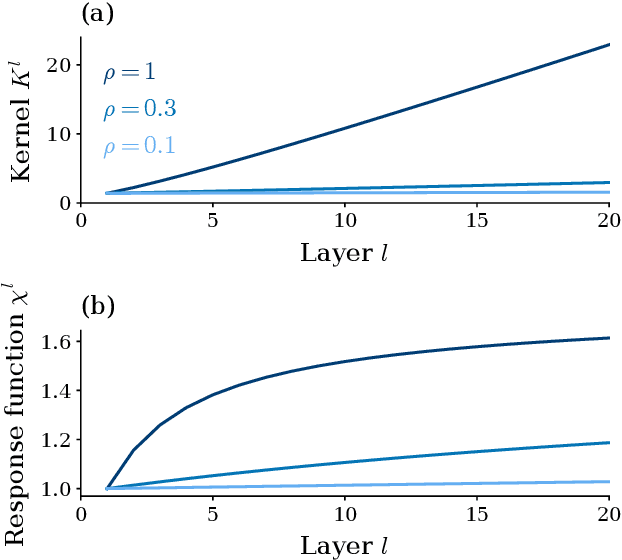
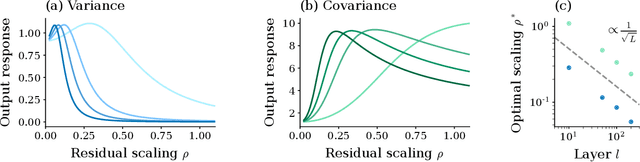
Residual networks (ResNets) have significantly better trainability and thus performance than feed-forward networks at large depth. Introducing skip connections facilitates signal propagation to deeper layers. In addition, previous works found that adding a scaling parameter for the residual branch further improves generalization performance. While they empirically identified a particularly beneficial range of values for this scaling parameter, the associated performance improvement and its universality across network hyperparameters yet need to be understood. For feed-forward networks (FFNets), finite-size theories have led to important insights with regard to signal propagation and hyperparameter tuning. We here derive a systematic finite-size theory for ResNets to study signal propagation and its dependence on the scaling for the residual branch. We derive analytical expressions for the response function, a measure for the network's sensitivity to inputs, and show that for deep networks the empirically found values for the scaling parameter lie within the range of maximal sensitivity. Furthermore, we obtain an analytical expression for the optimal scaling parameter that depends only weakly on other network hyperparameters, such as the weight variance, thereby explaining its universality across hyperparameters. Overall, this work provides a framework for theory-guided optimal scaling in ResNets and, more generally, provides the theoretical framework to study ResNets at finite widths.

Neuronal architecture extracts statistical temporal patterns

Neuronal systems need to process temporal signals. We here show how higher-order temporal (co-)fluctuations can be employed to represent and process information. Concretely, we demonstrate that a simple biologically inspired feedforward neuronal model is able to extract information from up to the third order cumulant to perform time series classification. This model relies on a weighted linear summation of synaptic inputs followed by a nonlinear gain function. Training both - the synaptic weights and the nonlinear gain function - exposes how the non-linearity allows for the transfer of higher order correlations to the mean, which in turn enables the synergistic use of information encoded in multiple cumulants to maximize the classification accuracy. The approach is demonstrated both on a synthetic and on real world datasets of multivariate time series. Moreover, we show that the biologically inspired architecture makes better use of the number of trainable parameters as compared to a classical machine-learning scheme. Our findings emphasize the benefit of biological neuronal architectures, paired with dedicated learning algorithms, for the processing of information embedded in higher-order statistical cumulants of temporal (co-)fluctuations.

Origami in N dimensions: How feed-forward networks manufacture linear separability

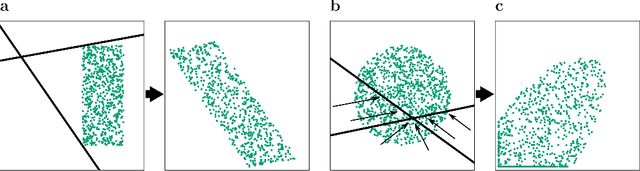
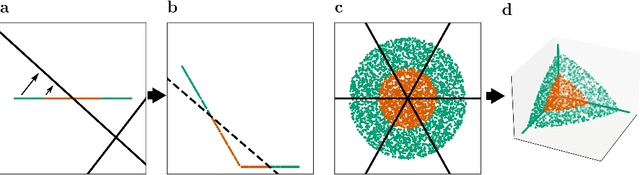
Neural networks can implement arbitrary functions. But, mechanistically, what are the tools at their disposal to construct the target? For classification tasks, the network must transform the data classes into a linearly separable representation in the final hidden layer. We show that a feed-forward architecture has one primary tool at hand to achieve this separability: progressive folding of the data manifold in unoccupied higher dimensions. The operation of folding provides a useful intuition in low-dimensions that generalizes to high ones. We argue that an alternative method based on shear, requiring very deep architectures, plays only a small role in real-world networks. The folding operation, however, is powerful as long as layers are wider than the data dimensionality, allowing efficient solutions by providing access to arbitrary regions in the distribution, such as data points of one class forming islands within the other classes. We argue that a link exists between the universal approximation property in ReLU networks and the fold-and-cut theorem (Demaine et al., 1998) dealing with physical paper folding. Based on the mechanistic insight, we predict that the progressive generation of separability is necessarily accompanied by neurons showing mixed selectivity and bimodal tuning curves. This is validated in a network trained on the poker hand task, showing the emergence of bimodal tuning curves during training. We hope that our intuitive picture of the data transformation in deep networks can help to provide interpretability, and discuss possible applications to the theory of convolutional networks, loss landscapes, and generalization. TL;DR: Shows that the internal processing of deep networks can be thought of as literal folding operations on the data distribution in the N-dimensional activation space. A link to a well-known theorem in origami theory is provided.

Decomposing neural networks as mappings of correlation functions

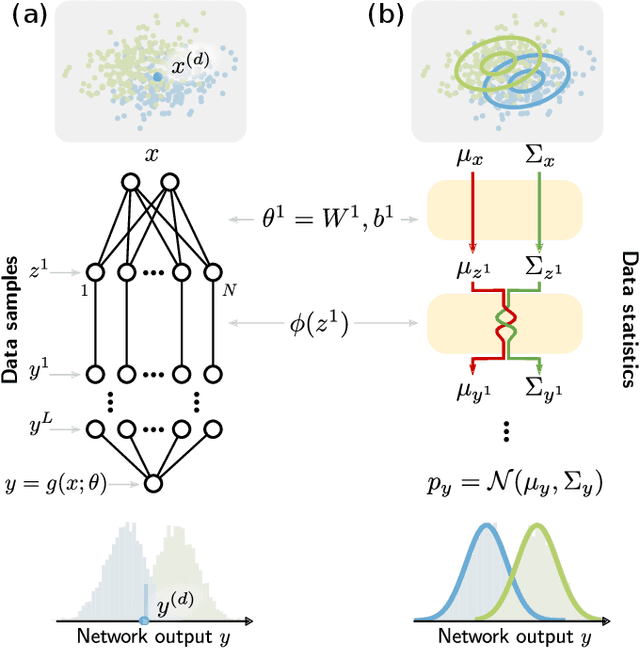
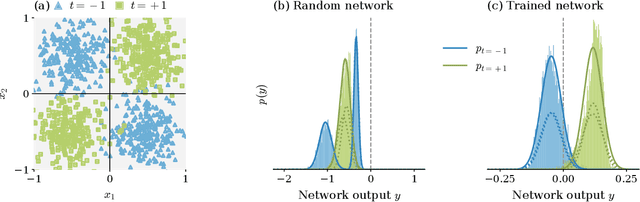
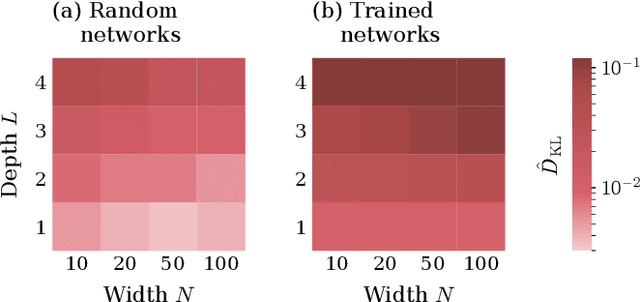
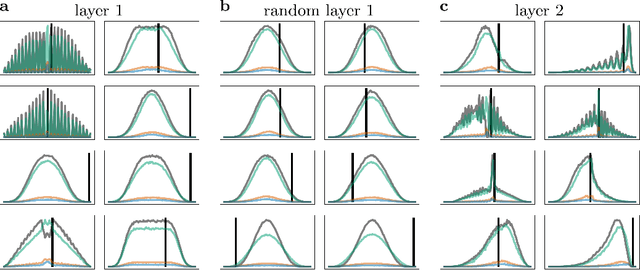
Understanding the functional principles of information processing in deep neural networks continues to be a challenge, in particular for networks with trained and thus non-random weights. To address this issue, we study the mapping between probability distributions implemented by a deep feed-forward network. We characterize this mapping as an iterated transformation of distributions, where the non-linearity in each layer transfers information between different orders of correlation functions. This allows us to identify essential statistics in the data, as well as different information representations that can be used by neural networks. Applied to an XOR task and to MNIST, we show that correlations up to second order predominantly capture the information processing in the internal layers, while the input layer also extracts higher-order correlations from the data. This analysis provides a quantitative and explainable perspective on classification.

Unified Field Theory for Deep and Recurrent Neural Networks

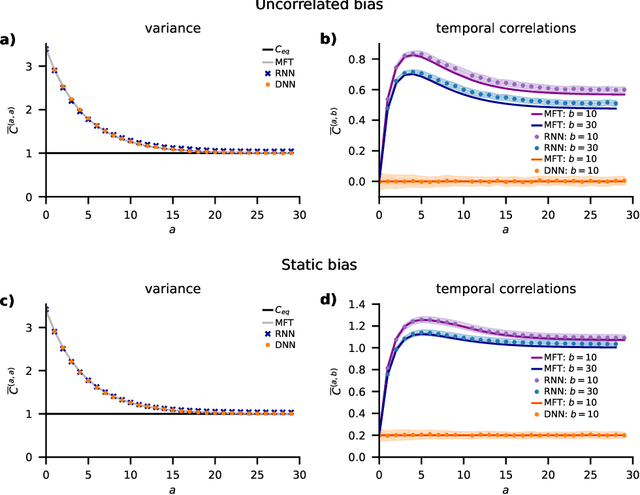
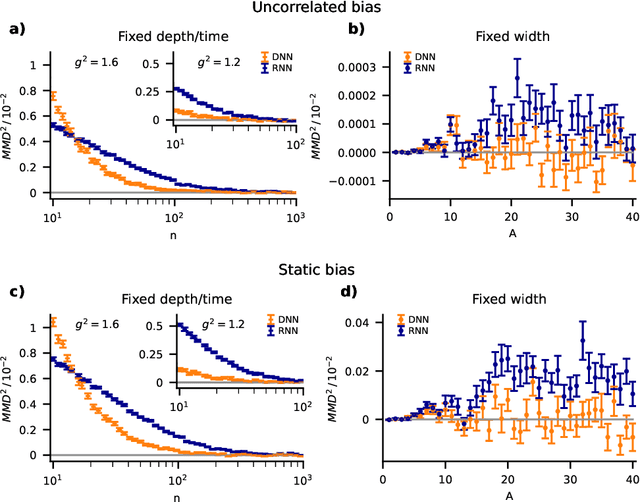
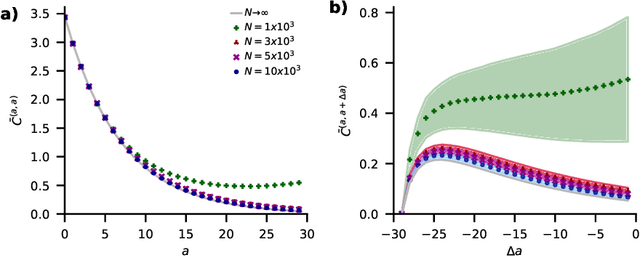
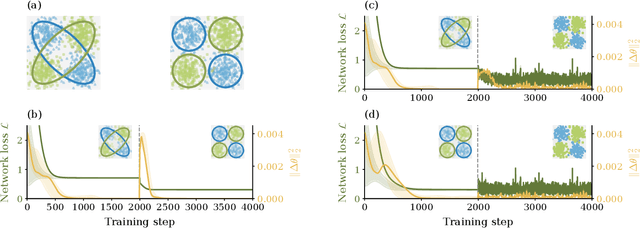
Understanding capabilities and limitations of different network architectures is of fundamental importance to machine learning. Bayesian inference on Gaussian processes has proven to be a viable approach for studying recurrent and deep networks in the limit of infinite layer width, $n\to\infty$. Here we present a unified and systematic derivation of the mean-field theory for both architectures that starts from first principles by employing established methods from statistical physics of disordered systems. The theory elucidates that while the mean-field equations are different with regard to their temporal structure, they yet yield identical Gaussian kernels when readouts are taken at a single time point or layer, respectively. Bayesian inference applied to classification then predicts identical performance and capabilities for the two architectures. Numerically, we find that convergence towards the mean-field theory is typically slower for recurrent networks than for deep networks and the convergence speed depends non-trivially on the parameters of the weight prior as well as the depth or number of time steps, respectively. Our method exposes that Gaussian processes are but the lowest order of a systematic expansion in $1/n$. The formalism thus paves the way to investigate the fundamental differences between recurrent and deep architectures at finite widths $n$.