Graph Neural Networks Do Not Always Oversmooth

Graph neural networks (GNNs) have emerged as powerful tools for processing relational data in applications. However, GNNs suffer from the problem of oversmoothing, the property that the features of all nodes exponentially converge to the same vector over layers, prohibiting the design of deep GNNs. In this work we study oversmoothing in graph convolutional networks (GCNs) by using their Gaussian process (GP) equivalence in the limit of infinitely many hidden features. By generalizing methods from conventional deep neural networks (DNNs), we can describe the distribution of features at the output layer of deep GCNs in terms of a GP: as expected, we find that typical parameter choices from the literature lead to oversmoothing. The theory, however, allows us to identify a new, nonoversmoothing phase: if the initial weights of the network have sufficiently large variance, GCNs do not oversmooth, and node features remain informative even at large depth. We demonstrate the validity of this prediction in finite-size GCNs by training a linear classifier on their output. Moreover, using the linearization of the GCN GP, we generalize the concept of propagation depth of information from DNNs to GCNs. This propagation depth diverges at the transition between the oversmoothing and non-oversmoothing phase. We test the predictions of our approach and find good agreement with finite-size GCNs. Initializing GCNs near the transition to the non-oversmoothing phase, we obtain networks which are both deep and expressive.

Decomposing neural networks as mappings of correlation functions

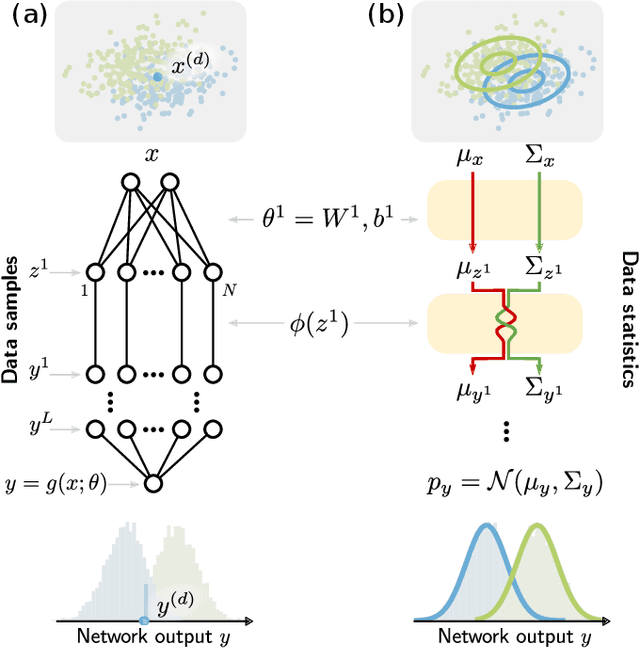
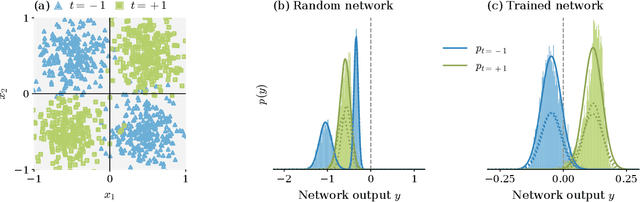
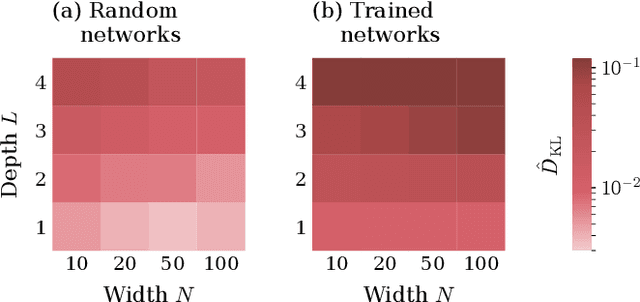
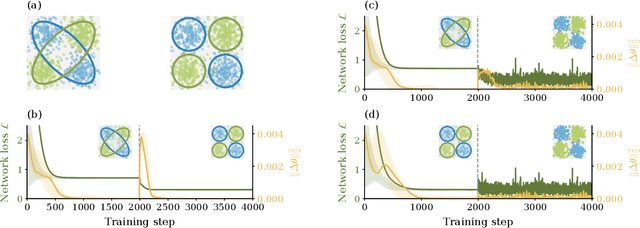
Understanding the functional principles of information processing in deep neural networks continues to be a challenge, in particular for networks with trained and thus non-random weights. To address this issue, we study the mapping between probability distributions implemented by a deep feed-forward network. We characterize this mapping as an iterated transformation of distributions, where the non-linearity in each layer transfers information between different orders of correlation functions. This allows us to identify essential statistics in the data, as well as different information representations that can be used by neural networks. Applied to an XOR task and to MNIST, we show that correlations up to second order predominantly capture the information processing in the internal layers, while the input layer also extracts higher-order correlations from the data. This analysis provides a quantitative and explainable perspective on classification.

Inference of a mesoscopic population model from population spike trains

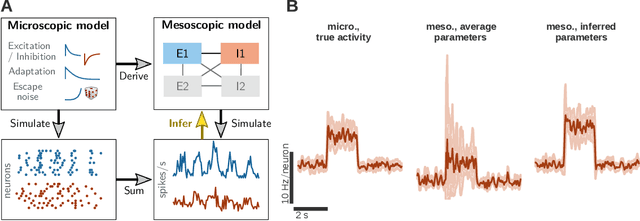
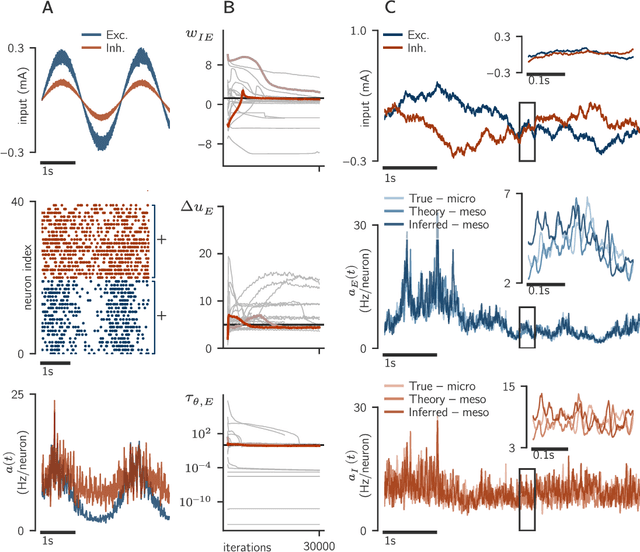
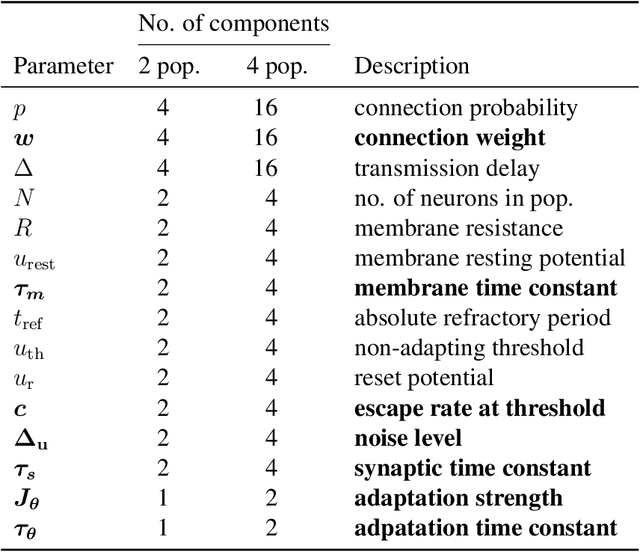
To understand how rich dynamics emerge in neural populations, we require models which exhibit a wide range of dynamics while remaining interpretable in terms of connectivity and single-neuron dynamics. However, it has been challenging to fit such mechanistic spiking networks at the single neuron scale to empirical population data. To close this gap, we propose to fit such data at a meso scale, using a mechanistic but low-dimensional and hence statistically tractable model. The mesoscopic representation is obtained by approximating a population of neurons as multiple homogeneous `pools' of neurons, and modelling the dynamics of the aggregate population activity within each pool. We derive the likelihood of both single-neuron and connectivity parameters given this activity, which can then be used to either optimize parameters by gradient ascent on the log-likelihood, or to perform Bayesian inference using Markov Chain Monte Carlo (MCMC) sampling. We illustrate this approach using a model of generalized integrate-and-fire neurons for which mesoscopic dynamics have been previously derived, and show that both single-neuron and connectivity parameters can be recovered from simulated data. In particular, our inference method extracts posterior correlations between model parameters, which define parameter subsets able to reproduce the data. We compute the Bayesian posterior for combinations of parameters using MCMC sampling and investigate how the approximations inherent to a mesoscopic population model impact the accuracy of the inferred single-neuron parameters.