From Kernels to Features: A Multi-Scale Adaptive Theory of Feature Learning

Theoretically describing feature learning in neural networks is crucial for understanding their expressive power and inductive biases, motivating various approaches. Some approaches describe network behavior after training through a simple change in kernel scale from initialization, resulting in a generalization power comparable to a Gaussian process. Conversely, in other approaches training results in the adaptation of the kernel to the data, involving complex directional changes to the kernel. While these approaches capture different facets of network behavior, their relationship and respective strengths across scaling regimes remains an open question. This work presents a theoretical framework of multi-scale adaptive feature learning bridging these approaches. Using methods from statistical mechanics, we derive analytical expressions for network output statistics which are valid across scaling regimes and in the continuum between them. A systematic expansion of the network's probability distribution reveals that mean-field scaling requires only a saddle-point approximation, while standard scaling necessitates additional correction terms. Remarkably, we find across regimes that kernel adaptation can be reduced to an effective kernel rescaling when predicting the mean network output of a linear network. However, even in this case, the multi-scale adaptive approach captures directional feature learning effects, providing richer insights than what could be recovered from a rescaling of the kernel alone.

Optimal signal propagation in ResNets through residual scaling

Residual networks (ResNets) have significantly better trainability and thus performance than feed-forward networks at large depth. Introducing skip connections facilitates signal propagation to deeper layers. In addition, previous works found that adding a scaling parameter for the residual branch further improves generalization performance. While they empirically identified a particularly beneficial range of values for this scaling parameter, the associated performance improvement and its universality across network hyperparameters yet need to be understood. For feed-forward networks (FFNets), finite-size theories have led to important insights with regard to signal propagation and hyperparameter tuning. We here derive a systematic finite-size theory for ResNets to study signal propagation and its dependence on the scaling for the residual branch. We derive analytical expressions for the response function, a measure for the network's sensitivity to inputs, and show that for deep networks the empirically found values for the scaling parameter lie within the range of maximal sensitivity. Furthermore, we obtain an analytical expression for the optimal scaling parameter that depends only weakly on other network hyperparameters, such as the weight variance, thereby explaining its universality across hyperparameters. Overall, this work provides a framework for theory-guided optimal scaling in ResNets and, more generally, provides the theoretical framework to study ResNets at finite widths.

Decomposing neural networks as mappings of correlation functions

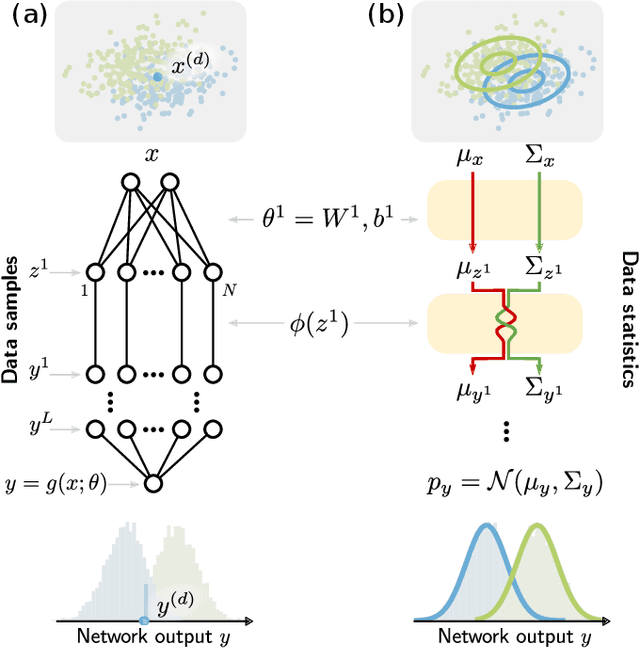
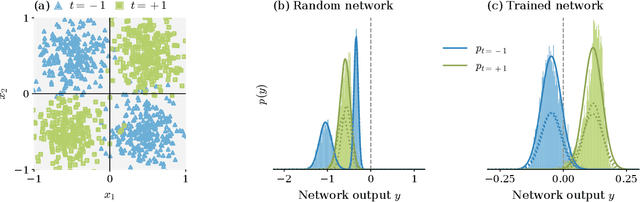
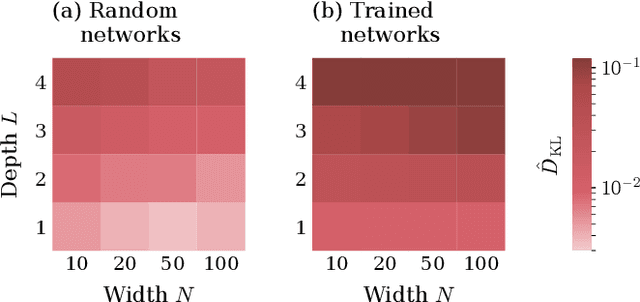
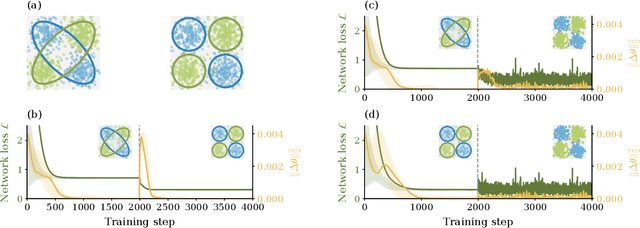
Understanding the functional principles of information processing in deep neural networks continues to be a challenge, in particular for networks with trained and thus non-random weights. To address this issue, we study the mapping between probability distributions implemented by a deep feed-forward network. We characterize this mapping as an iterated transformation of distributions, where the non-linearity in each layer transfers information between different orders of correlation functions. This allows us to identify essential statistics in the data, as well as different information representations that can be used by neural networks. Applied to an XOR task and to MNIST, we show that correlations up to second order predominantly capture the information processing in the internal layers, while the input layer also extracts higher-order correlations from the data. This analysis provides a quantitative and explainable perspective on classification.