Statistical physics, Bayesian inference and neural information processing

Lecture notes from the course given by Professor Sara A. Solla at the Les Houches summer school on "Statistical physics of Machine Learning". The notes discuss neural information processing through the lens of Statistical Physics. Contents include Bayesian inference and its connection to a Gibbs description of learning and generalization, Generalized Linear Models as a controlled alternative to backpropagation through time, and linear and non-linear techniques for dimensionality reduction.

Neuronal architecture extracts statistical temporal patterns

Neuronal systems need to process temporal signals. We here show how higher-order temporal (co-)fluctuations can be employed to represent and process information. Concretely, we demonstrate that a simple biologically inspired feedforward neuronal model is able to extract information from up to the third order cumulant to perform time series classification. This model relies on a weighted linear summation of synaptic inputs followed by a nonlinear gain function. Training both - the synaptic weights and the nonlinear gain function - exposes how the non-linearity allows for the transfer of higher order correlations to the mean, which in turn enables the synergistic use of information encoded in multiple cumulants to maximize the classification accuracy. The approach is demonstrated both on a synthetic and on real world datasets of multivariate time series. Moreover, we show that the biologically inspired architecture makes better use of the number of trainable parameters as compared to a classical machine-learning scheme. Our findings emphasize the benefit of biological neuronal architectures, paired with dedicated learning algorithms, for the processing of information embedded in higher-order statistical cumulants of temporal (co-)fluctuations.

Path classification by stochastic linear recurrent neural networks

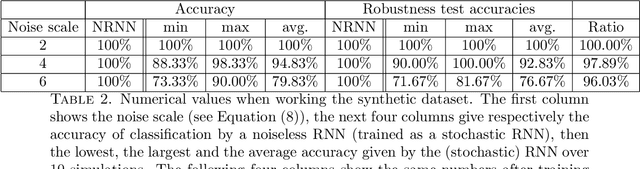
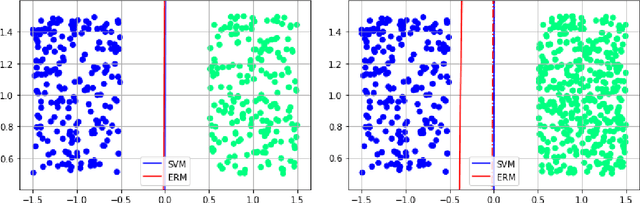
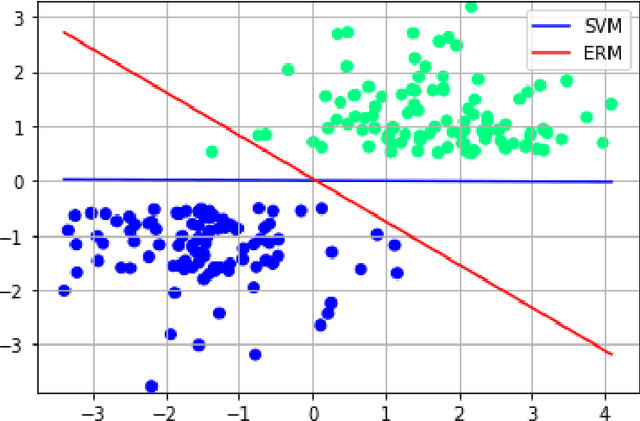
We investigate the functioning of a classifying biological neural network from the perspective of statistical learning theory, modelled, in a simplified setting, as a continuous-time stochastic recurrent neural network (RNN) with identity activation function. In the purely stochastic (robust) regime, we give a generalisation error bound that holds with high probability, thus showing that the empirical risk minimiser is the best-in-class hypothesis. We show that RNNs retain a partial signature of the paths they are fed as the unique information exploited for training and classification tasks. We argue that these RNNs are easy to train and robust and back these observations with numerical experiments on both synthetic and real data. We also exhibit a trade-off phenomenon between accuracy and robustness.

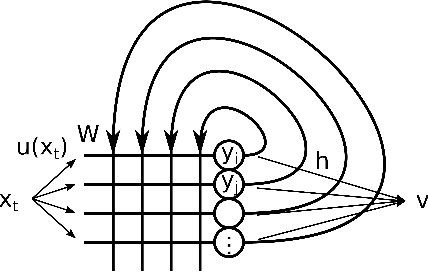
Unfolding recurrence by Green's functions for optimized reservoir computing

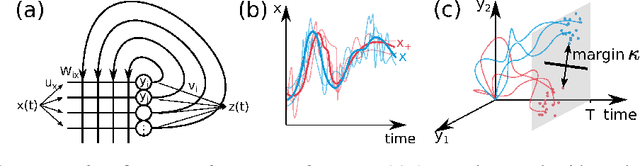
Cortical networks are strongly recurrent, and neurons have intrinsic temporal dynamics. This sets them apart from deep feed-forward networks. Despite the tremendous progress in the application of feed-forward networks and their theoretical understanding, it remains unclear how the interplay of recurrence and non-linearities in recurrent cortical networks contributes to their function. The purpose of this work is to present a solvable recurrent network model that links to feed forward networks. By perturbative methods we transform the time-continuous, recurrent dynamics into an effective feed-forward structure of linear and non-linear temporal kernels. The resulting analytical expressions allow us to build optimal time-series classifiers from random reservoir networks. Firstly, this allows us to optimize not only the readout vectors, but also the input projection, demonstrating a strong potential performance gain. Secondly, the analysis exposes how the second order stimulus statistics is a crucial element that interacts with the non-linearity of the dynamics and boosts performance.