Unfolding recurrence by Green's functions for optimized reservoir computing
Paper and Code
Oct 14, 2020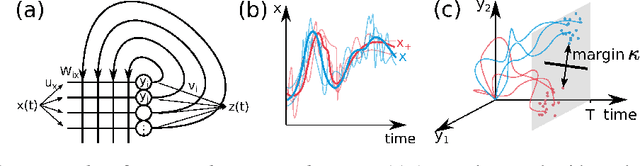


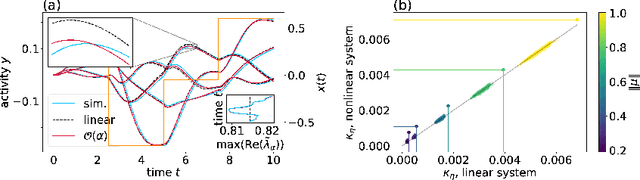
Cortical networks are strongly recurrent, and neurons have intrinsic temporal dynamics. This sets them apart from deep feed-forward networks. Despite the tremendous progress in the application of feed-forward networks and their theoretical understanding, it remains unclear how the interplay of recurrence and non-linearities in recurrent cortical networks contributes to their function. The purpose of this work is to present a solvable recurrent network model that links to feed forward networks. By perturbative methods we transform the time-continuous, recurrent dynamics into an effective feed-forward structure of linear and non-linear temporal kernels. The resulting analytical expressions allow us to build optimal time-series classifiers from random reservoir networks. Firstly, this allows us to optimize not only the readout vectors, but also the input projection, demonstrating a strong potential performance gain. Secondly, the analysis exposes how the second order stimulus statistics is a crucial element that interacts with the non-linearity of the dynamics and boosts performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge