Neuronal architecture extracts statistical temporal patterns

Neuronal systems need to process temporal signals. We here show how higher-order temporal (co-)fluctuations can be employed to represent and process information. Concretely, we demonstrate that a simple biologically inspired feedforward neuronal model is able to extract information from up to the third order cumulant to perform time series classification. This model relies on a weighted linear summation of synaptic inputs followed by a nonlinear gain function. Training both - the synaptic weights and the nonlinear gain function - exposes how the non-linearity allows for the transfer of higher order correlations to the mean, which in turn enables the synergistic use of information encoded in multiple cumulants to maximize the classification accuracy. The approach is demonstrated both on a synthetic and on real world datasets of multivariate time series. Moreover, we show that the biologically inspired architecture makes better use of the number of trainable parameters as compared to a classical machine-learning scheme. Our findings emphasize the benefit of biological neuronal architectures, paired with dedicated learning algorithms, for the processing of information embedded in higher-order statistical cumulants of temporal (co-)fluctuations.

Unfolding recurrence by Green's functions for optimized reservoir computing

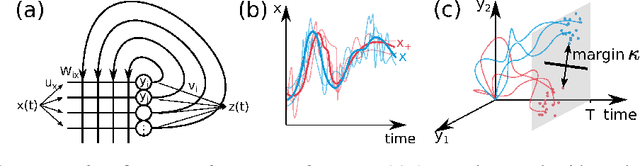
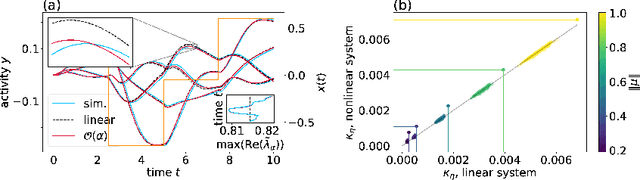
Cortical networks are strongly recurrent, and neurons have intrinsic temporal dynamics. This sets them apart from deep feed-forward networks. Despite the tremendous progress in the application of feed-forward networks and their theoretical understanding, it remains unclear how the interplay of recurrence and non-linearities in recurrent cortical networks contributes to their function. The purpose of this work is to present a solvable recurrent network model that links to feed forward networks. By perturbative methods we transform the time-continuous, recurrent dynamics into an effective feed-forward structure of linear and non-linear temporal kernels. The resulting analytical expressions allow us to build optimal time-series classifiers from random reservoir networks. Firstly, this allows us to optimize not only the readout vectors, but also the input projection, demonstrating a strong potential performance gain. Secondly, the analysis exposes how the second order stimulus statistics is a crucial element that interacts with the non-linearity of the dynamics and boosts performance.

Capacity of the covariance perceptron

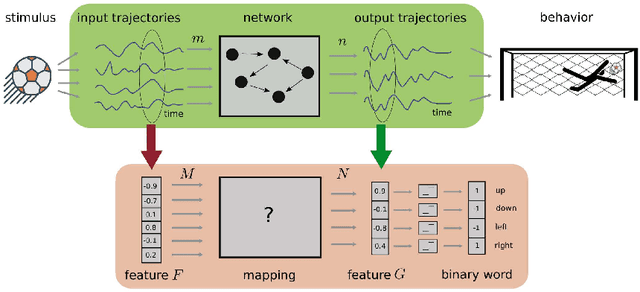
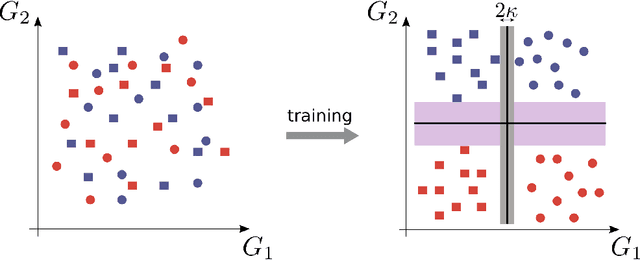
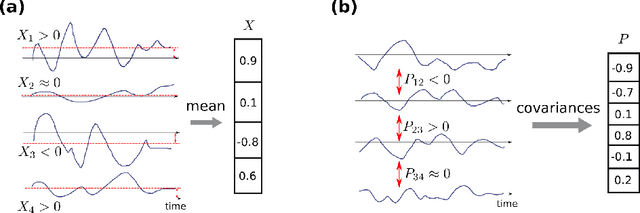
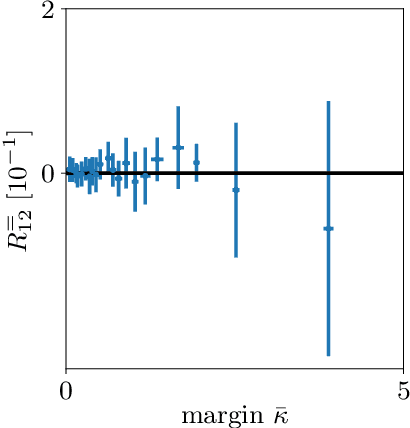
The classical perceptron is a simple neural network that performs a binary classification by a linear mapping between static inputs and outputs and application of a threshold. For small inputs, neural networks in a stationary state also perform an effectively linear input-output transformation, but of an entire time series. Choosing the temporal mean of the time series as the feature for classification, the linear transformation of the network with subsequent thresholding is equivalent to the classical perceptron. Here we show that choosing covariances of time series as the feature for classification maps the neural network to what we call a 'covariance perceptron'; a bilinear mapping between covariances. By extending Gardner's theory of connections to this bilinear problem, using a replica symmetric mean-field theory, we compute the pattern and information capacities of the covariance perceptron in the infinite-size limit. Closed-form expressions reveal superior pattern capacity in the binary classification task compared to the classical perceptron in the case of a high-dimensional input and low-dimensional output. For less convergent networks, the mean perceptron classifies a larger number of stimuli. However, since covariances span a much larger input and output space than means, the amount of stored information in the covariance perceptron exceeds the classical counterpart. For strongly convergent connectivity it is superior by a factor equal to the number of input neurons. Theoretical calculations are validated numerically for finite size systems using a gradient-based optimization of a soft-margin, as well as numerical solvers for the NP hard quadratically constrained quadratic programming problem, to which training can be mapped.

Propagation of moments in Hawkes networks

The present paper provides a mathematical description of high-order moments of spiking activity in a recurrently-connected network of Hawkes processes. It extends previous studies that have explored the case of a (linear) Hawkes network driven by deterministic rate functions to the case of a stimulation by external inputs (rate functions or spike trains) with arbitrary correlation structure. Our approach describes the spatio-temporal filtering induced by the afferent and recurrent connectivities using operators of the input moments. This algebraic viewpoint provides intuition about how the network ingredients shape the input-output mapping for moments, as well as cumulants.

Bayesian estimation for large scale multivariate Ornstein-Uhlenbeck model of brain connectivity

Estimation of reliable whole-brain connectivity is a crucial step towards the use of connectivity information in quantitative approaches to the study of neuropsychiatric disorders. When estimating brain connectivity a challenge is imposed by the paucity of time samples and the large dimensionality of the measurements. Bayesian estimation methods for network models offer a number of advantages in this context but are not commonly employed. Here we compare three different estimation methods for the multivariate Ornstein-Uhlenbeck model, that has recently gained some popularity for characterizing whole-brain connectivity. We first show that a Bayesian estimation of model parameters assuming uniform priors is equivalent to an application of the method of moments. Then, using synthetic data, we show that the Bayesian estimate scales poorly with number of nodes in the network as compared to an iterative Lyapunov optimization. In particular when the network size is in the order of that used for whole-brain studies (about 100 nodes) the Bayesian method needs about eight times more time samples than Lyapunov method in order to achieve similar estimation accuracy. We also show that the higher estimation accuracy of Lyapunov method is reflected in a much better classification of individuals based on the estimated connectivity from a real dataset of BOLD fMRI. Finally we show that the poor accuracy of Bayesian method is due to numerical errors, when the imaginary part of the connectivity estimate gets large compared to its real part.