Path classification by stochastic linear recurrent neural networks
Paper and Code
Aug 06, 2021
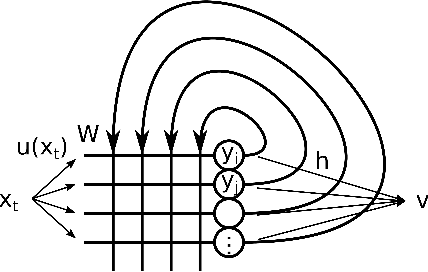
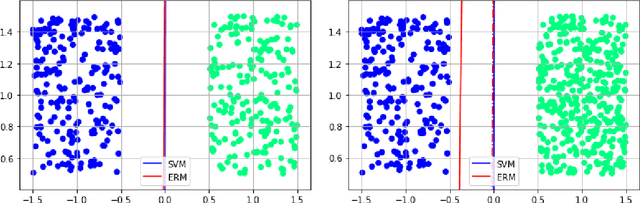
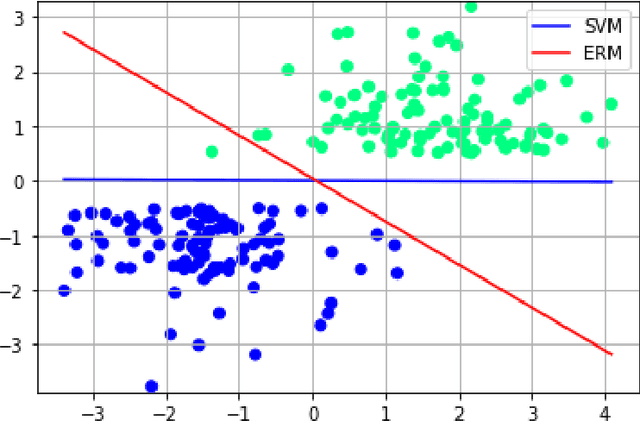
We investigate the functioning of a classifying biological neural network from the perspective of statistical learning theory, modelled, in a simplified setting, as a continuous-time stochastic recurrent neural network (RNN) with identity activation function. In the purely stochastic (robust) regime, we give a generalisation error bound that holds with high probability, thus showing that the empirical risk minimiser is the best-in-class hypothesis. We show that RNNs retain a partial signature of the paths they are fed as the unique information exploited for training and classification tasks. We argue that these RNNs are easy to train and robust and back these observations with numerical experiments on both synthetic and real data. We also exhibit a trade-off phenomenon between accuracy and robustness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge