Should Under-parameterized Student Networks Copy or Average Teacher Weights?

Any continuous function $f^*$ can be approximated arbitrarily well by a neural network with sufficiently many neurons $k$. We consider the case when $f^*$ itself is a neural network with one hidden layer and $k$ neurons. Approximating $f^*$ with a neural network with $n< k$ neurons can thus be seen as fitting an under-parameterized "student" network with $n$ neurons to a "teacher" network with $k$ neurons. As the student has fewer neurons than the teacher, it is unclear, whether each of the $n$ student neurons should copy one of the teacher neurons or rather average a group of teacher neurons. For shallow neural networks with erf activation function and for the standard Gaussian input distribution, we prove that "copy-average" configurations are critical points if the teacher's incoming vectors are orthonormal and its outgoing weights are unitary. Moreover, the optimum among such configurations is reached when $n-1$ student neurons each copy one teacher neuron and the $n$-th student neuron averages the remaining $k-n+1$ teacher neurons. For the student network with $n=1$ neuron, we provide additionally a closed-form solution of the non-trivial critical point(s) for commonly used activation functions through solving an equivalent constrained optimization problem. Empirically, we find for the erf activation function that gradient flow converges either to the optimal copy-average critical point or to another point where each student neuron approximately copies a different teacher neuron. Finally, we find similar results for the ReLU activation function, suggesting that the optimal solution of underparameterized networks has a universal structure.

Statistical physics, Bayesian inference and neural information processing

Lecture notes from the course given by Professor Sara A. Solla at the Les Houches summer school on "Statistical physics of Machine Learning". The notes discuss neural information processing through the lens of Statistical Physics. Contents include Bayesian inference and its connection to a Gibbs description of learning and generalization, Generalized Linear Models as a controlled alternative to backpropagation through time, and linear and non-linear techniques for dimensionality reduction.

MLPGradientFlow: going with the flow of multilayer perceptrons (and finding minima fast and accurately)

MLPGradientFlow is a software package to solve numerically the gradient flow differential equation $\dot \theta = -\nabla \mathcal L(\theta; \mathcal D)$, where $\theta$ are the parameters of a multi-layer perceptron, $\mathcal D$ is some data set, and $\nabla \mathcal L$ is the gradient of a loss function. We show numerically that adaptive first- or higher-order integration methods based on Runge-Kutta schemes have better accuracy and convergence speed than gradient descent with the Adam optimizer. However, we find Newton's method and approximations like BFGS preferable to find fixed points (local and global minima of $\mathcal L$) efficiently and accurately. For small networks and data sets, gradients are usually computed faster than in pytorch and Hessian are computed at least $5\times$ faster. Additionally, the package features an integrator for a teacher-student setup with bias-free, two-layer networks trained with standard Gaussian input in the limit of infinite data. The code is accessible at https://github.com/jbrea/MLPGradientFlow.jl.

Deep Linear Networks Dynamics: Low-Rank Biases Induced by Initialization Scale and L2 Regularization

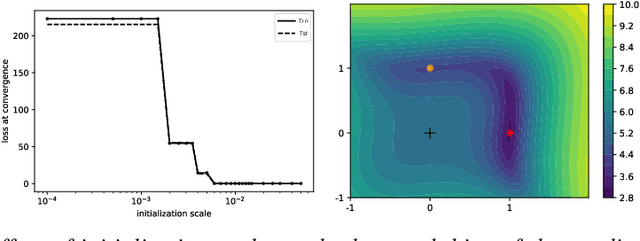
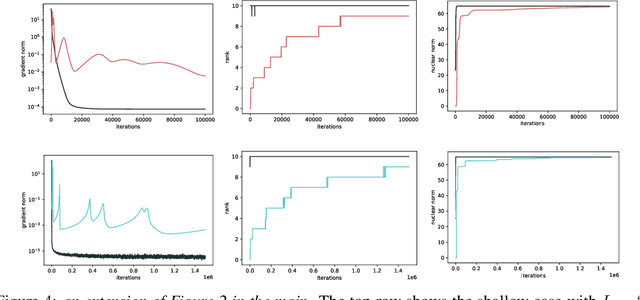
For deep linear networks (DLN), various hyperparameters alter the dynamics of training dramatically. We investigate how the rank of the linear map found by gradient descent is affected by (1) the initialization norm and (2) the addition of $L_{2}$ regularization on the parameters. For (1), we study two regimes: (1a) the linear/lazy regime, for large norm initialization; (1b) a \textquotedbl saddle-to-saddle\textquotedbl{} regime for small initialization norm. In the (1a) setting, the dynamics of a DLN of any depth is similar to that of a standard linear model, without any low-rank bias. In the (1b) setting, we conjecture that throughout training, gradient descent approaches a sequence of saddles, each corresponding to linear maps of increasing rank, until reaching a minimal rank global minimum. We support this conjecture with a partial proof and some numerical experiments. For (2), we show that adding a $L_{2}$ regularization on the parameters corresponds to the addition to the cost of a $L_{p}$-Schatten (quasi)norm on the linear map with $p=\frac{2}{L}$ (for a depth-$L$ network), leading to a stronger low-rank bias as $L$ grows. The effect of $L_{2}$ regularization on the loss surface depends on the depth: for shallow networks, all critical points are either strict saddles or global minima, whereas for deep networks, some local minima appear. We numerically observe that these local minima can generalize better than global ones in some settings.

Geometry of the Loss Landscape in Overparameterized Neural Networks: Symmetries and Invariances

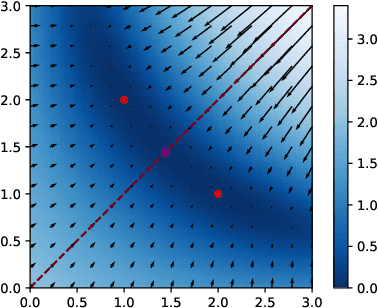
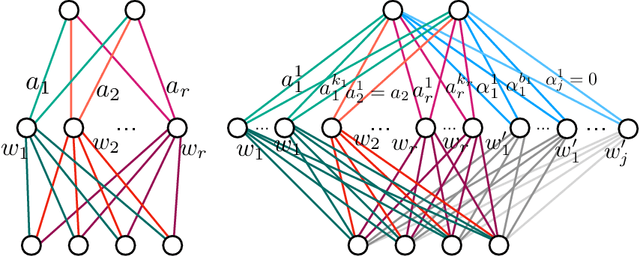
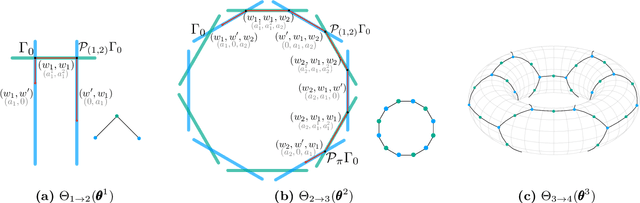
We study how permutation symmetries in overparameterized multi-layer neural networks generate `symmetry-induced' critical points. Assuming a network with $ L $ layers of minimal widths $ r_1^*, \ldots, r_{L-1}^* $ reaches a zero-loss minimum at $ r_1^*! \cdots r_{L-1}^*! $ isolated points that are permutations of one another, we show that adding one extra neuron to each layer is sufficient to connect all these previously discrete minima into a single manifold. For a two-layer overparameterized network of width $ r^*+ h =: m $ we explicitly describe the manifold of global minima: it consists of $ T(r^*, m) $ affine subspaces of dimension at least $ h $ that are connected to one another. For a network of width $m$, we identify the number $G(r,m)$ of affine subspaces containing only symmetry-induced critical points that are related to the critical points of a smaller network of width $r<r^*$. Via a combinatorial analysis, we derive closed-form formulas for $ T $ and $ G $ and show that the number of symmetry-induced critical subspaces dominates the number of affine subspaces forming the global minima manifold in the mildly overparameterized regime (small $ h $) and vice versa in the vastly overparameterized regime ($h \gg r^*$). Our results provide new insights into the minimization of the non-convex loss function of overparameterized neural networks.

Kernel Alignment Risk Estimator: Risk Prediction from Training Data

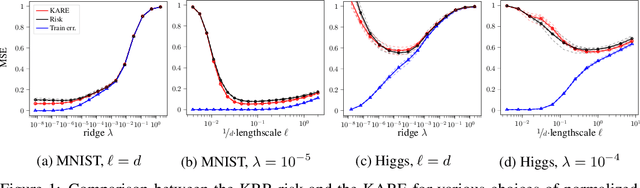
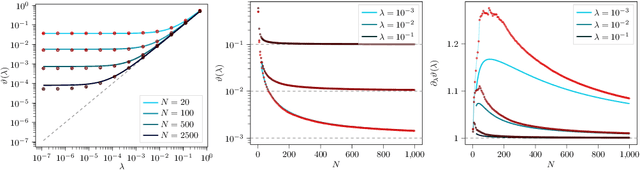
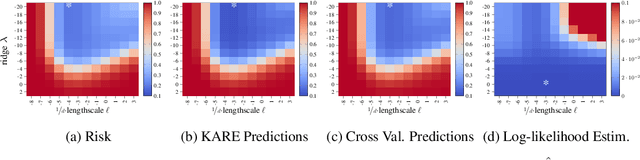
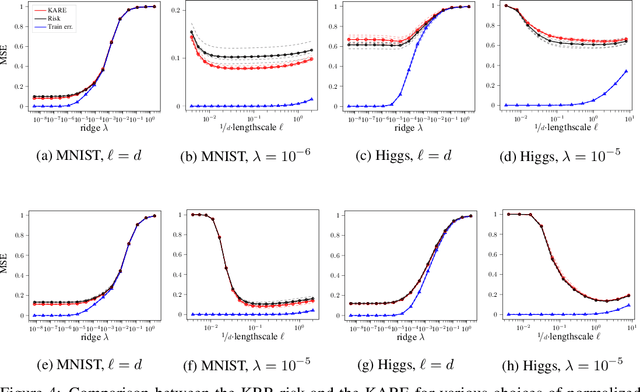
We study the risk (i.e. generalization error) of Kernel Ridge Regression (KRR) for a kernel $K$ with ridge $\lambda>0$ and i.i.d. observations. For this, we introduce two objects: the Signal Capture Threshold (SCT) and the Kernel Alignment Risk Estimator (KARE). The SCT $\vartheta_{K,\lambda}$ is a function of the data distribution: it can be used to identify the components of the data that the KRR predictor captures, and to approximate the (expected) KRR risk. This then leads to a KRR risk approximation by the KARE $\rho_{K, \lambda}$, an explicit function of the training data, agnostic of the true data distribution. We phrase the regression problem in a functional setting. The key results then follow from a finite-size analysis of the Stieltjes transform of general Wishart random matrices. Under a natural universality assumption (that the KRR moments depend asymptotically on the first two moments of the observations) we capture the mean and variance of the KRR predictor. We numerically investigate our findings on the Higgs and MNIST datasets for various classical kernels: the KARE gives an excellent approximation of the risk, thus supporting our universality assumption. Using the KARE, one can compare choices of Kernels and hyperparameters directly from the training set. The KARE thus provides a promising data-dependent procedure to select Kernels that generalize well.

Implicit Regularization of Random Feature Models

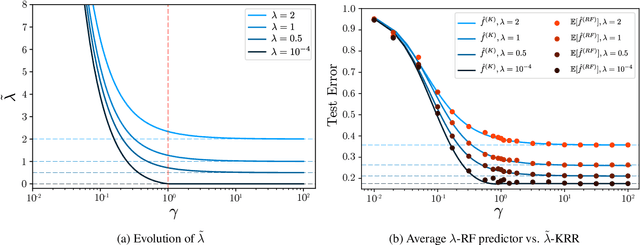
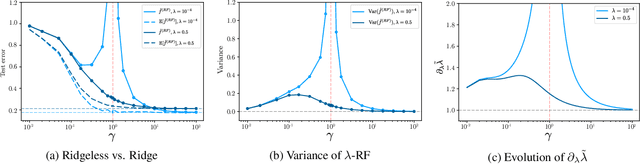
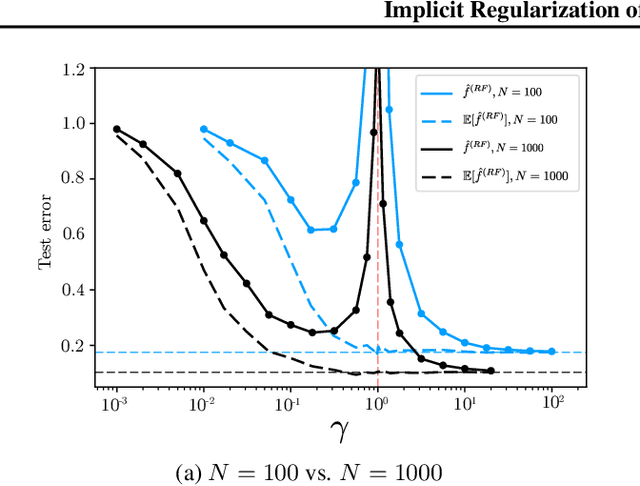
Random Feature (RF) models are used as efficient parametric approximations of kernel methods. We investigate, by means of random matrix theory, the connection between Gaussian RF models and Kernel Ridge Regression (KRR). For a Gaussian RF model with $P$ features, $N$ data points, and a ridge $\lambda$, we show that the average (i.e. expected) RF predictor is close to a KRR predictor with an effective ridge $\tilde{\lambda}$. We show that $\tilde{\lambda} > \lambda$ and $\tilde{\lambda} \searrow \lambda$ monotonically as $P$ grows, thus revealing the implicit regularization effect of finite RF sampling. We then compare the risk (i.e. test error) of the $\tilde{\lambda}$-KRR predictor with the average risk of the $\lambda$-RF predictor and obtain a precise and explicit bound on their difference. Finally, we empirically find an extremely good agreement between the test errors of the average $\lambda$-RF predictor and $\tilde{\lambda}$-KRR predictor.