Feature Learning in $L_{2}$-regularized DNNs: Attraction/Repulsion and Sparsity

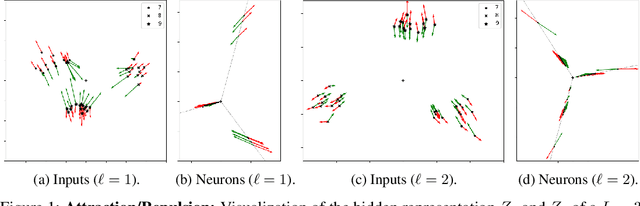
We study the loss surface of DNNs with $L_{2}$ regularization. We show that the loss in terms of the parameters can be reformulated into a loss in terms of the layerwise activations $Z_{\ell}$ of the training set. This reformulation reveals the dynamics behind feature learning: each hidden representations $Z_{\ell}$ are optimal w.r.t. to an attraction/repulsion problem and interpolate between the input and output representations, keeping as little information from the input as necessary to construct the activation of the next layer. For positively homogeneous non-linearities, the loss can be further reformulated in terms of the covariances of the hidden representations, which takes the form of a partially convex optimization over a convex cone. This second reformulation allows us to prove a sparsity result for homogeneous DNNs: any local minimum of the $L_{2}$-regularized loss can be achieved with at most $N(N+1)$ neurons in each hidden layer (where $N$ is the size of the training set). We show that this bound is tight by giving an example of a local minimum which requires $N^{2}/4$ hidden neurons. But we also observe numerically that in more traditional settings much less than $N^{2}$ neurons are required to reach the minima.

Deep Linear Networks Dynamics: Low-Rank Biases Induced by Initialization Scale and L2 Regularization

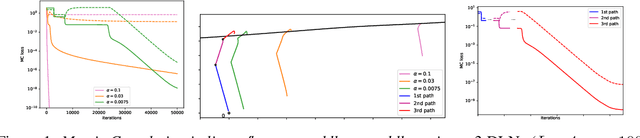
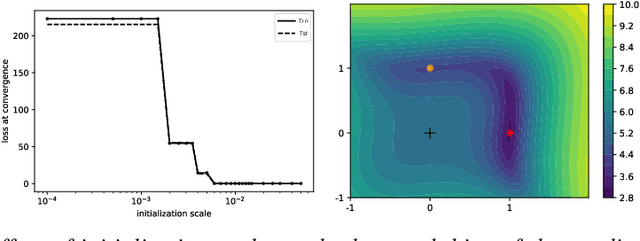
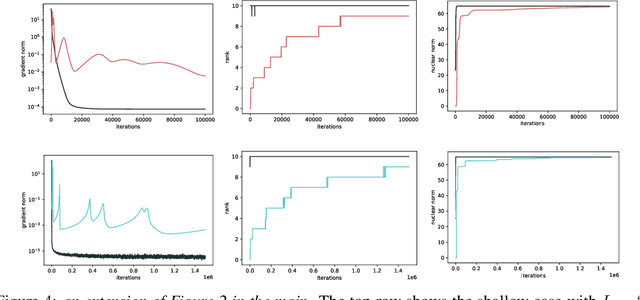
For deep linear networks (DLN), various hyperparameters alter the dynamics of training dramatically. We investigate how the rank of the linear map found by gradient descent is affected by (1) the initialization norm and (2) the addition of $L_{2}$ regularization on the parameters. For (1), we study two regimes: (1a) the linear/lazy regime, for large norm initialization; (1b) a \textquotedbl saddle-to-saddle\textquotedbl{} regime for small initialization norm. In the (1a) setting, the dynamics of a DLN of any depth is similar to that of a standard linear model, without any low-rank bias. In the (1b) setting, we conjecture that throughout training, gradient descent approaches a sequence of saddles, each corresponding to linear maps of increasing rank, until reaching a minimal rank global minimum. We support this conjecture with a partial proof and some numerical experiments. For (2), we show that adding a $L_{2}$ regularization on the parameters corresponds to the addition to the cost of a $L_{p}$-Schatten (quasi)norm on the linear map with $p=\frac{2}{L}$ (for a depth-$L$ network), leading to a stronger low-rank bias as $L$ grows. The effect of $L_{2}$ regularization on the loss surface depends on the depth: for shallow networks, all critical points are either strict saddles or global minima, whereas for deep networks, some local minima appear. We numerically observe that these local minima can generalize better than global ones in some settings.

Smart Proofs via Smart Contracts: Succinct and Informative Mathematical Derivations via Decentralized Markets

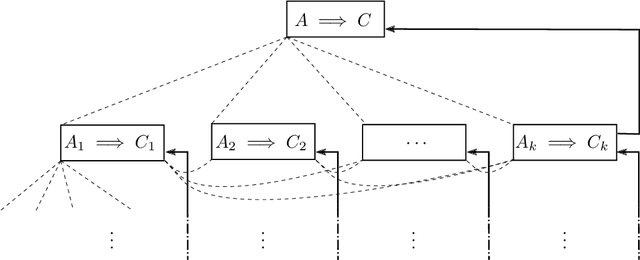
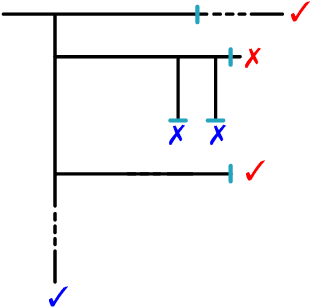
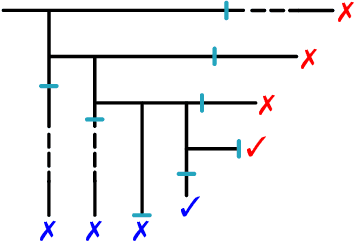
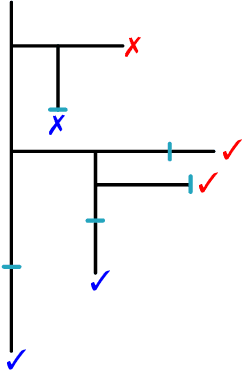
Modern mathematics is built on the idea that proofs should be translatable into formal proofs, whose validity is an objective question, decidable by a computer. Yet, in practice, proofs are informal and may omit many details. An agent considers a proof valid if they trust that it could be expanded into a machine-verifiable proof. A proof's validity can thus become a subjective matter and lead to a debate, which may be difficult to settle. Hence, while the concept of valid proof is well-defined, the process to establish validity is itself a complex multi-agent problem. We introduce the SPRIG protocol. SPRIG allows agents to propose and verify succinct and informative proofs in a decentralized fashion; the trust is established by agents being able to request more details in the proof steps; debates, if they arise, must isolate details of proofs and, if they persist, go down to machine-level details, where they are automatically settled. A structure of bounties and stakes is set to incentivize agents to act in good faith. We propose a game-theoretic discussion of SPRIG, showing how agents with various types of information interact, leading to a proof tree with an appropriate level of detail and to the invalidation of wrong proofs, and we discuss resilience against various attacks. We then analyze a simplified model, characterize its equilibria and compute the agents' level of trust. SPRIG is designed to run as a smart contract on a blockchain platform. This allows anonymous agents to participate in the verification debate, and to contribute with their information. The smart contract mediates the interactions, settles debates, and guarantees that bounties and stakes are paid as specified. SPRIG enables new applications, such as the issuance of bounties for open problems, and the creation of derivatives markets, allowing agents to inject more information pertaining to proofs.

Kernel Alignment Risk Estimator: Risk Prediction from Training Data

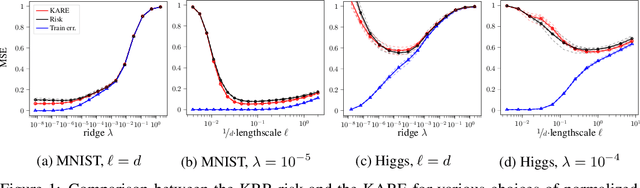
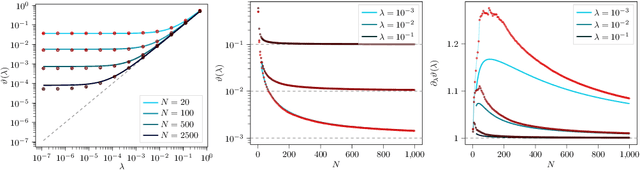
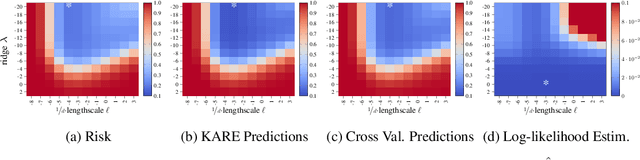
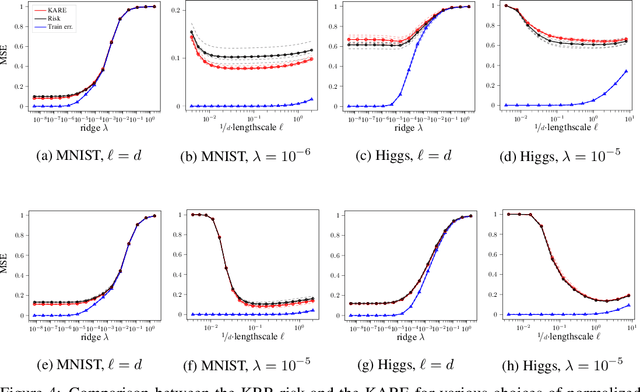
We study the risk (i.e. generalization error) of Kernel Ridge Regression (KRR) for a kernel $K$ with ridge $\lambda>0$ and i.i.d. observations. For this, we introduce two objects: the Signal Capture Threshold (SCT) and the Kernel Alignment Risk Estimator (KARE). The SCT $\vartheta_{K,\lambda}$ is a function of the data distribution: it can be used to identify the components of the data that the KRR predictor captures, and to approximate the (expected) KRR risk. This then leads to a KRR risk approximation by the KARE $\rho_{K, \lambda}$, an explicit function of the training data, agnostic of the true data distribution. We phrase the regression problem in a functional setting. The key results then follow from a finite-size analysis of the Stieltjes transform of general Wishart random matrices. Under a natural universality assumption (that the KRR moments depend asymptotically on the first two moments of the observations) we capture the mean and variance of the KRR predictor. We numerically investigate our findings on the Higgs and MNIST datasets for various classical kernels: the KARE gives an excellent approximation of the risk, thus supporting our universality assumption. Using the KARE, one can compare choices of Kernels and hyperparameters directly from the training set. The KARE thus provides a promising data-dependent procedure to select Kernels that generalize well.

Implicit Regularization of Random Feature Models

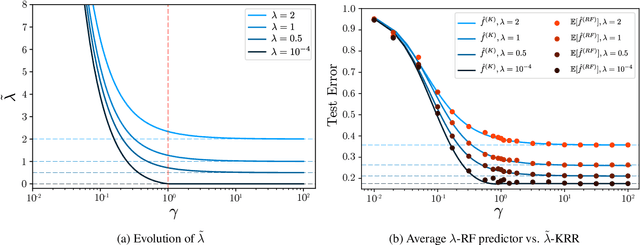
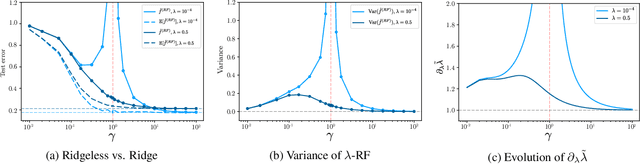
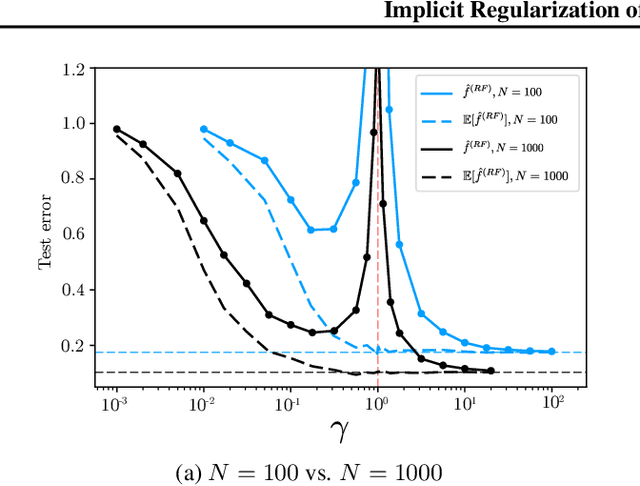
Random Feature (RF) models are used as efficient parametric approximations of kernel methods. We investigate, by means of random matrix theory, the connection between Gaussian RF models and Kernel Ridge Regression (KRR). For a Gaussian RF model with $P$ features, $N$ data points, and a ridge $\lambda$, we show that the average (i.e. expected) RF predictor is close to a KRR predictor with an effective ridge $\tilde{\lambda}$. We show that $\tilde{\lambda} > \lambda$ and $\tilde{\lambda} \searrow \lambda$ monotonically as $P$ grows, thus revealing the implicit regularization effect of finite RF sampling. We then compare the risk (i.e. test error) of the $\tilde{\lambda}$-KRR predictor with the average risk of the $\lambda$-RF predictor and obtain a precise and explicit bound on their difference. Finally, we empirically find an extremely good agreement between the test errors of the average $\lambda$-RF predictor and $\tilde{\lambda}$-KRR predictor.

The asymptotic spectrum of the Hessian of DNN throughout training

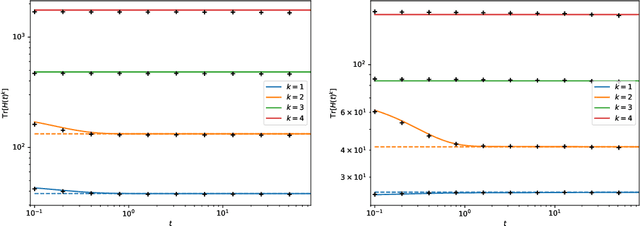
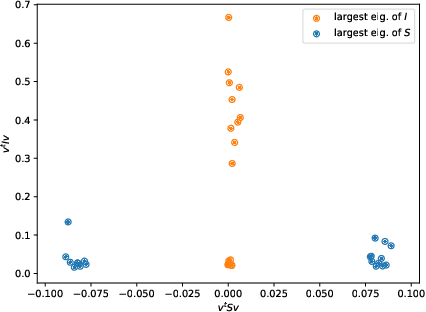
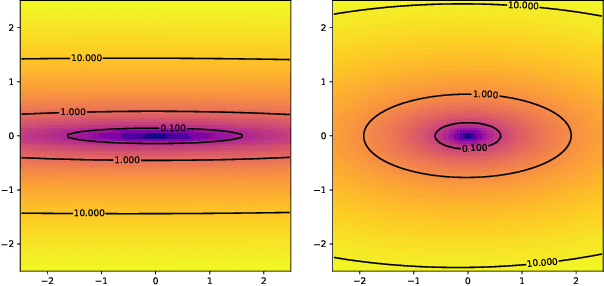
The dynamics of DNNs during gradient descent is described by the so-called Neural Tangent Kernel (NTK). In this article, we show that the NTK allows one to gain precise insight into the Hessian of the cost of DNNs: we obtain a full characterization of the asymptotics of the spectrum of the Hessian, at initialization and during training.

Freeze and Chaos for DNNs: an NTK view of Batch Normalization, Checkerboard and Boundary Effects

In this paper, we analyze a number of architectural features of Deep Neural Networks (DNNs), using the so-called Neural Tangent Kernel (NTK). The NTK describes the training trajectory and generalization of DNNs in the infinite-width limit. In this limit, we show that for (fully-connected) DNNs, as the depth grows, two regimes appear: "freeze" (also known as "order"), where the (scaled) NTK converges to a constant (slowing convergence), and "chaos", where it converges to a Kronecker delta (limiting generalization). We show that when using the scaled ReLU as a nonlinearity, we naturally end up in the "freeze". We show that Batch Normalization (BN) avoids the freeze regime by reducing the importance of the constant mode in the NTK. A similar effect is obtained by normalizing the nonlinearity which moves the network to the chaotic regime. We uncover the same "freeze" and "chaos" modes in Deep Deconvolutional Networks (DC-NNs). The "freeze" regime is characterized by checkerboard patterns in the image space in addition to the constant modes in input space. Finally, we introduce a new NTK-based parametrization to eliminate border artifacts and we propose a layer-dependent learning rate to improve the convergence of DC-NNs. We illustrate our findings by training DCGANs using our setup. When trained in the "freeze" regime, we see that the generator collapses to a checkerboard mode. We also demonstrate numerically that the generator collapse can be avoided and that good quality samples can be obtained, by tuning the nonlinearity to reach the "chaos" regime (without using batch normalization).

Scaling description of generalization with number of parameters in deep learning

We provide a description for the evolution of the generalization performance of fixed-depth fully-connected deep neural networks as a function of the number of parameters $N$. We observe that increasing $N$ at fixed depth reduces the fluctuations of the output function $f_N$ induced by initial conditions, with $\Vert f_N-{\bar f}_N\Vert\sim N^{-1/4}$ where ${\bar f}_N$ denotes an average over initial conditions, and we explain this asymptotic behavior in terms of the fluctuations of the so-called Neural Tangent Kernel that controls the dynamics of the output function. For the task of classification, we predict these fluctuations to increase the test error $\epsilon$ as $\epsilon_{N}-\epsilon_{\infty}\sim N^{-1/2} + \mathcal{O}( N^{-3/4})$: this prediction is consistent with our empirical results on the MNIST dataset and it explains the puzzling observation that the predictive power of deep networks improves as the number of fitting parameters grows. This asymptotic description breaks down at a so-called jamming transition which takes place at a critical $N=N^*$, below which the training error is non-zero. In the absence of regularization, we observe an apparent divergence $\Vert f_N\Vert\sim (N-N^*)^{-\alpha}$ and provide a simple argument suggesting $\alpha=1$, consistent with empirical observations. This result leads to a plausible explanation for the cusp in test error known to occur at $N^*$. In practice, our analysis suggests that optimal generalization can be reached by ensemble averaging output functions at $N$ fixed slightly above $N^*$.

Neural Tangent Kernel: Convergence and Generalization in Neural Networks

At initialization, artificial neural networks (ANNs) are equivalent to Gaussian processes in the infinite-width limit, thus connecting them to kernel methods. We prove that the evolution of an ANN during training can also be described by a kernel: during gradient descent on the parameters of an ANN, the network function $f_\theta$ (which maps input vectors to output vectors) follows the kernel gradient of the functional cost (which is convex, in contrast to the parameter cost) w.r.t. a new kernel: the Neural Tangent Kernel (NTK). This kernel is central to describe the generalization features of ANNs. While the NTK is random at initialization and varies during training, in the infinite-width limit it converges to an explicit limiting kernel and it stays constant during training. This makes it possible to study the training of ANNs in function space instead of parameter space. Convergence of the training can then be related to the positive-definiteness of the limiting NTK. We prove the positive-definiteness of the limiting NTK when the data is supported on the sphere and the non-linearity is non-polynomial. We then focus on the setting of least-squares regression and show that in the infinite-width limit, the network function $f_\theta$ follows a linear differential equation during training. The convergence is fastest along the largest kernel principal components of the input data with respect to the NTK, hence suggesting a theoretical motivation for early stopping. Finally we study the NTK numerically, observe its behavior for wide networks, and compare it to the infinite-width limit.