Smart Proofs via Smart Contracts: Succinct and Informative Mathematical Derivations via Decentralized Markets

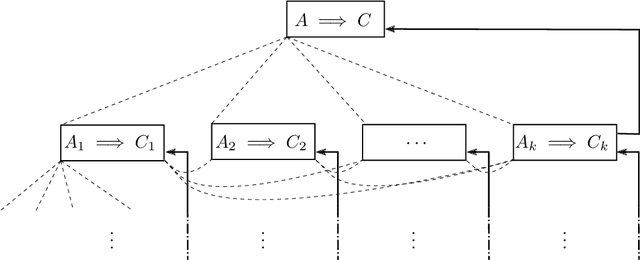
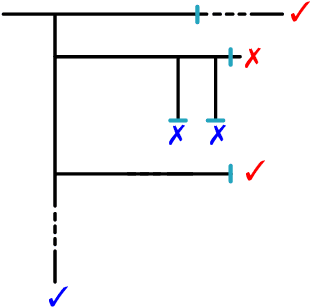
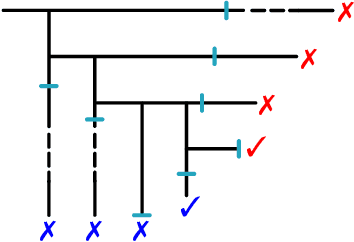
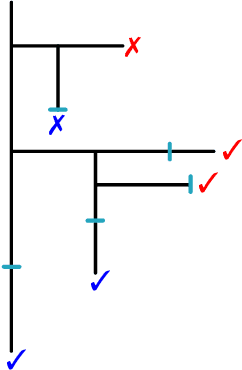
Modern mathematics is built on the idea that proofs should be translatable into formal proofs, whose validity is an objective question, decidable by a computer. Yet, in practice, proofs are informal and may omit many details. An agent considers a proof valid if they trust that it could be expanded into a machine-verifiable proof. A proof's validity can thus become a subjective matter and lead to a debate, which may be difficult to settle. Hence, while the concept of valid proof is well-defined, the process to establish validity is itself a complex multi-agent problem. We introduce the SPRIG protocol. SPRIG allows agents to propose and verify succinct and informative proofs in a decentralized fashion; the trust is established by agents being able to request more details in the proof steps; debates, if they arise, must isolate details of proofs and, if they persist, go down to machine-level details, where they are automatically settled. A structure of bounties and stakes is set to incentivize agents to act in good faith. We propose a game-theoretic discussion of SPRIG, showing how agents with various types of information interact, leading to a proof tree with an appropriate level of detail and to the invalidation of wrong proofs, and we discuss resilience against various attacks. We then analyze a simplified model, characterize its equilibria and compute the agents' level of trust. SPRIG is designed to run as a smart contract on a blockchain platform. This allows anonymous agents to participate in the verification debate, and to contribute with their information. The smart contract mediates the interactions, settles debates, and guarantees that bounties and stakes are paid as specified. SPRIG enables new applications, such as the issuance of bounties for open problems, and the creation of derivatives markets, allowing agents to inject more information pertaining to proofs.

Discovering Cyclic Causal Models by Independent Components Analysis

We generalize Shimizu et al's (2006) ICA-based approach for discovering linear non-Gaussian acyclic (LiNGAM) Structural Equation Models (SEMs) from causally sufficient, continuous-valued observational data. By relaxing the assumption that the generating SEM's graph is acyclic, we solve the more general problem of linear non-Gaussian (LiNG) SEM discovery. LiNG discovery algorithms output the distribution equivalence class of SEMs which, in the large sample limit, represents the population distribution. We apply a LiNG discovery algorithm to simulated data. Finally, we give sufficient conditions under which only one of the SEMs in the output class is 'stable'.

Causal discovery of linear acyclic models with arbitrary distributions

An important task in data analysis is the discovery of causal relationships between observed variables. For continuous-valued data, linear acyclic causal models are commonly used to model the data-generating process, and the inference of such models is a well-studied problem. However, existing methods have significant limitations. Methods based on conditional independencies (Spirtes et al. 1993; Pearl 2000) cannot distinguish between independence-equivalent models, whereas approaches purely based on Independent Component Analysis (Shimizu et al. 2006) are inapplicable to data which is partially Gaussian. In this paper, we generalize and combine the two approaches, to yield a method able to learn the model structure in many cases for which the previous methods provide answers that are either incorrect or are not as informative as possible. We give exact graphical conditions for when two distinct models represent the same family of distributions, and empirically demonstrate the power of our method through thorough simulations.