Discovering Cyclic Causal Models with Latent Variables: A General SAT-Based Procedure

We present a very general approach to learning the structure of causal models based on d-separation constraints, obtained from any given set of overlapping passive observational or experimental data sets. The procedure allows for both directed cycles (feedback loops) and the presence of latent variables. Our approach is based on a logical representation of causal pathways, which permits the integration of quite general background knowledge, and inference is performed using a Boolean satisfiability (SAT) solver. The procedure is complete in that it exhausts the available information on whether any given edge can be determined to be present or absent, and returns "unknown" otherwise. Many existing constraint-based causal discovery algorithms can be seen as special cases, tailored to circumstances in which one or more restricting assumptions apply. Simulations illustrate the effect of these assumptions on discovery and how the present algorithm scales.

Causal Discovery of Linear Cyclic Models from Multiple Experimental Data Sets with Overlapping Variables

Much of scientific data is collected as randomized experiments intervening on some and observing other variables of interest. Quite often, a given phenomenon is investigated in several studies, and different sets of variables are involved in each study. In this article we consider the problem of integrating such knowledge, inferring as much as possible concerning the underlying causal structure with respect to the union of observed variables from such experimental or passive observational overlapping data sets. We do not assume acyclicity or joint causal sufficiency of the underlying data generating model, but we do restrict the causal relationships to be linear and use only second order statistics of the data. We derive conditions for full model identifiability in the most generic case, and provide novel techniques for incorporating an assumption of faithfulness to aid in inference. In each case we seek to establish what is and what is not determined by the data at hand.

Estimating a Causal Order among Groups of Variables in Linear Models

The machine learning community has recently devoted much attention to the problem of inferring causal relationships from statistical data. Most of this work has focused on uncovering connections among scalar random variables. We generalize existing methods to apply to collections of multi-dimensional random vectors, focusing on techniques applicable to linear models. The performance of the resulting algorithms is evaluated and compared in simulations, which show that our methods can, in many cases, provide useful information on causal relationships even for relatively small sample sizes.

Discovery of non-gaussian linear causal models using ICA

In recent years, several methods have been proposed for the discovery of causal structure from non-experimental data (Spirtes et al. 2000; Pearl 2000). Such methods make various assumptions on the data generating process to facilitate its identification from purely observational data. Continuing this line of research, we show how to discover the complete causal structure of continuous-valued data, under the assumptions that (a) the data generating process is linear, (b) there are no unobserved confounders, and (c) disturbance variables have non-gaussian distributions of non-zero variances. The solution relies on the use of the statistical method known as independent component analysis (ICA), and does not require any pre-specified time-ordering of the variables. We provide a complete Matlab package for performing this LiNGAM analysis (short for Linear Non-Gaussian Acyclic Model), and demonstrate the effectiveness of the method using artificially generated data.

Discovering Cyclic Causal Models by Independent Components Analysis

We generalize Shimizu et al's (2006) ICA-based approach for discovering linear non-Gaussian acyclic (LiNGAM) Structural Equation Models (SEMs) from causally sufficient, continuous-valued observational data. By relaxing the assumption that the generating SEM's graph is acyclic, we solve the more general problem of linear non-Gaussian (LiNG) SEM discovery. LiNG discovery algorithms output the distribution equivalence class of SEMs which, in the large sample limit, represents the population distribution. We apply a LiNG discovery algorithm to simulated data. Finally, we give sufficient conditions under which only one of the SEMs in the output class is 'stable'.

Causal discovery of linear acyclic models with arbitrary distributions

An important task in data analysis is the discovery of causal relationships between observed variables. For continuous-valued data, linear acyclic causal models are commonly used to model the data-generating process, and the inference of such models is a well-studied problem. However, existing methods have significant limitations. Methods based on conditional independencies (Spirtes et al. 1993; Pearl 2000) cannot distinguish between independence-equivalent models, whereas approaches purely based on Independent Component Analysis (Shimizu et al. 2006) are inapplicable to data which is partially Gaussian. In this paper, we generalize and combine the two approaches, to yield a method able to learn the model structure in many cases for which the previous methods provide answers that are either incorrect or are not as informative as possible. We give exact graphical conditions for when two distinct models represent the same family of distributions, and empirically demonstrate the power of our method through thorough simulations.

Bayesian Discovery of Linear Acyclic Causal Models

Methods for automated discovery of causal relationships from non-interventional data have received much attention recently. A widely used and well understood model family is given by linear acyclic causal models (recursive structural equation models). For Gaussian data both constraint-based methods (Spirtes et al., 1993; Pearl, 2000) (which output a single equivalence class) and Bayesian score-based methods (Geiger and Heckerman, 1994) (which assign relative scores to the equivalence classes) are available. On the contrary, all current methods able to utilize non-Gaussianity in the data (Shimizu et al., 2006; Hoyer et al., 2008) always return only a single graph or a single equivalence class, and so are fundamentally unable to express the degree of certainty attached to that output. In this paper we develop a Bayesian score-based approach able to take advantage of non-Gaussianity when estimating linear acyclic causal models, and we empirically demonstrate that, at least on very modest size networks, its accuracy is as good as or better than existing methods. We provide a complete code package (in R) which implements all algorithms and performs all of the analysis provided in the paper, and hope that this will further the application of these methods to solving causal inference problems.

Noisy-OR Models with Latent Confounding

Given a set of experiments in which varying subsets of observed variables are subject to intervention, we consider the problem of identifiability of causal models exhibiting latent confounding. While identifiability is trivial when each experiment intervenes on a large number of variables, the situation is more complicated when only one or a few variables are subject to intervention per experiment. For linear causal models with latent variables Hyttinen et al. (2010) gave precise conditions for when such data are sufficient to identify the full model. While their result cannot be extended to discrete-valued variables with arbitrary cause-effect relationships, we show that a similar result can be obtained for the class of causal models whose conditional probability distributions are restricted to a `noisy-OR' parameterization. We further show that identification is preserved under an extension of the model that allows for negative influences, and present learning algorithms that we test for accuracy, scalability and robustness.

DirectLiNGAM: A direct method for learning a linear non-Gaussian structural equation model

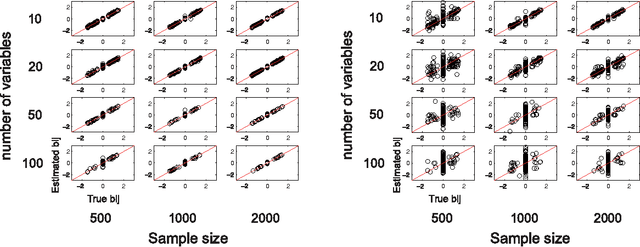
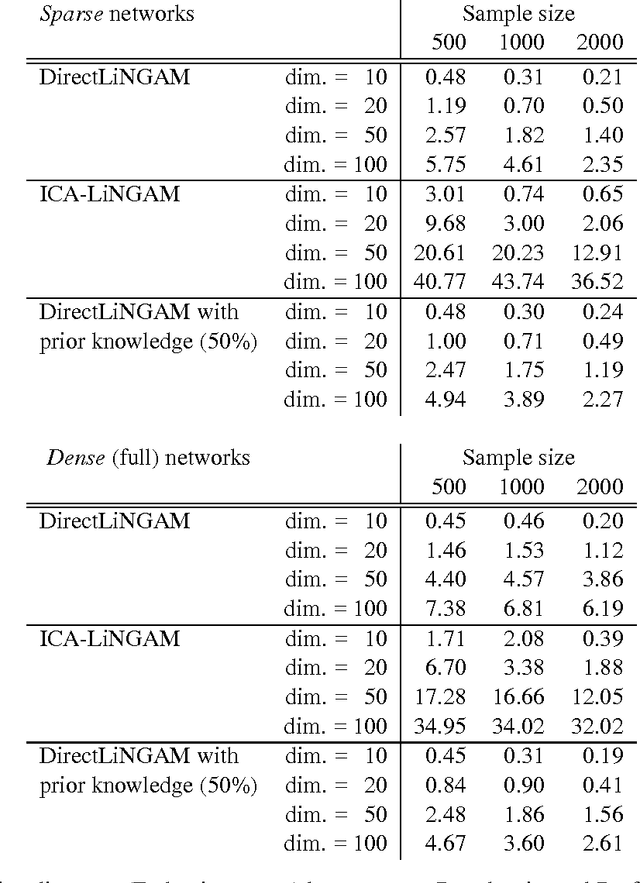
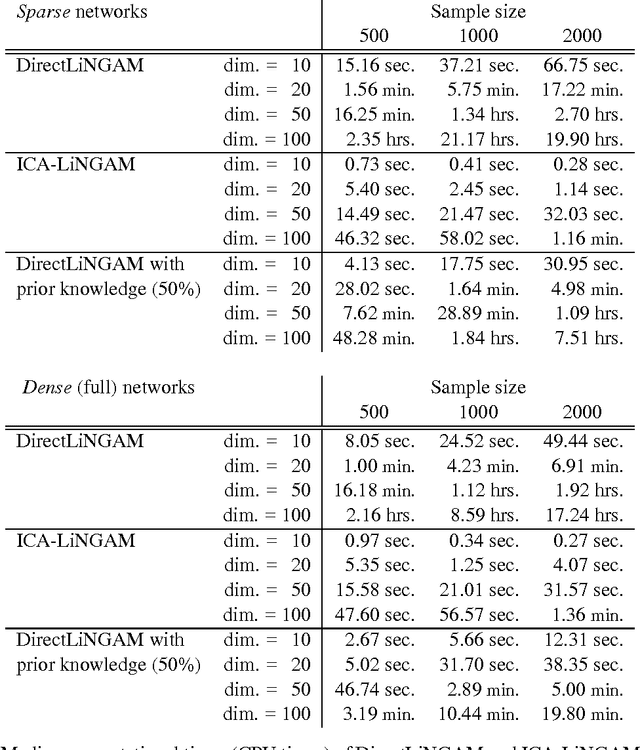
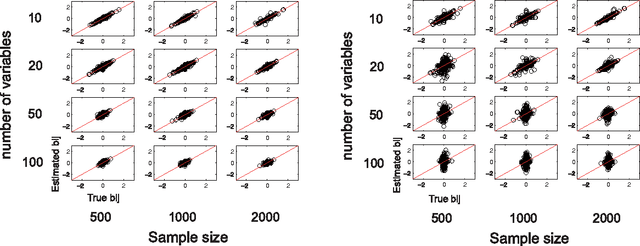
Structural equation models and Bayesian networks have been widely used to analyze causal relations between continuous variables. In such frameworks, linear acyclic models are typically used to model the data-generating process of variables. Recently, it was shown that use of non-Gaussianity identifies the full structure of a linear acyclic model, i.e., a causal ordering of variables and their connection strengths, without using any prior knowledge on the network structure, which is not the case with conventional methods. However, existing estimation methods are based on iterative search algorithms and may not converge to a correct solution in a finite number of steps. In this paper, we propose a new direct method to estimate a causal ordering and connection strengths based on non-Gaussianity. In contrast to the previous methods, our algorithm requires no algorithmic parameters and is guaranteed to converge to the right solution within a small fixed number of steps if the data strictly follows the model.

Telling cause from effect based on high-dimensional observations

We describe a method for inferring linear causal relations among multi-dimensional variables. The idea is to use an asymmetry between the distributions of cause and effect that occurs if both the covariance matrix of the cause and the structure matrix mapping cause to the effect are independently chosen. The method works for both stochastic and deterministic causal relations, provided that the dimensionality is sufficiently high (in some experiments, 5 was enough). It is applicable to Gaussian as well as non-Gaussian data.