Causal Discovery in a Binary Exclusive-or Skew Acyclic Model: BExSAM

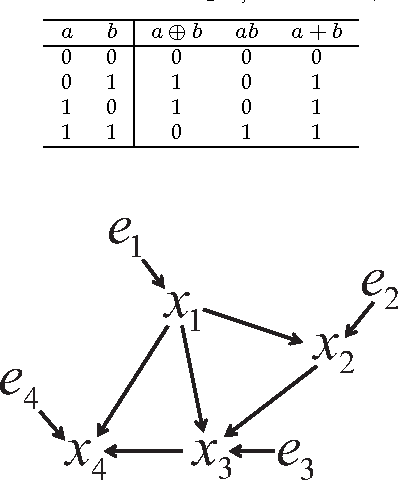
Discovering causal relations among observed variables in a given data set is a major objective in studies of statistics and artificial intelligence. Recently, some techniques to discover a unique causal model have been explored based on non-Gaussianity of the observed data distribution. However, most of these are limited to continuous data. In this paper, we present a novel causal model for binary data and propose an efficient new approach to deriving the unique causal model governing a given binary data set under skew distributions of external binary noises. Experimental evaluation shows excellent performance for both artificial and real world data sets.

Identifiability of an Integer Modular Acyclic Additive Noise Model and its Causal Structure Discovery

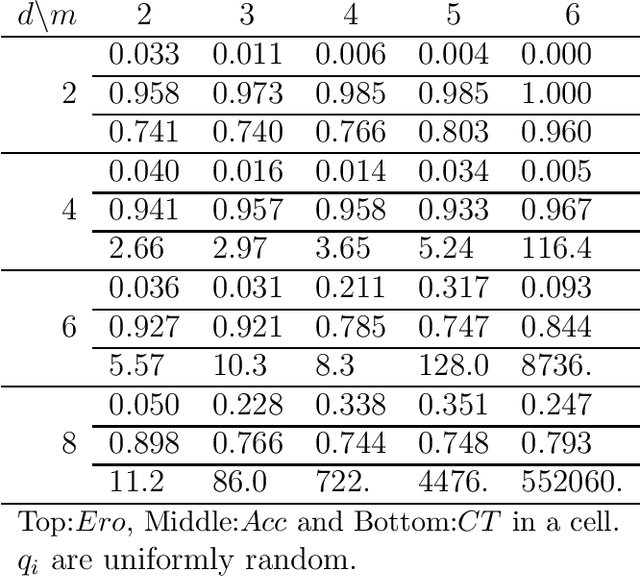
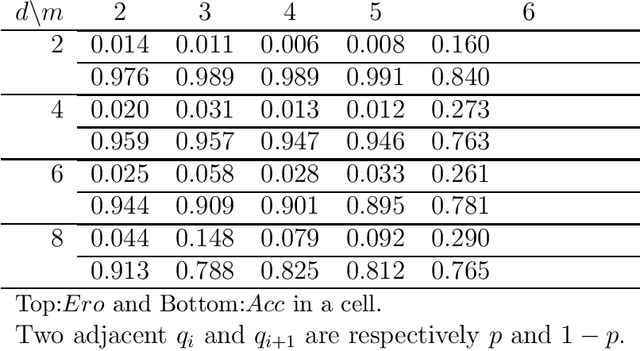
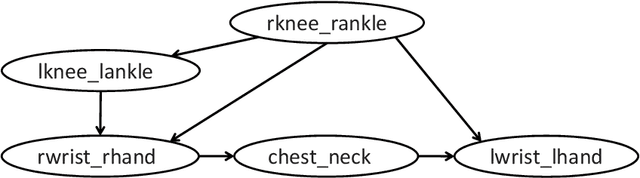
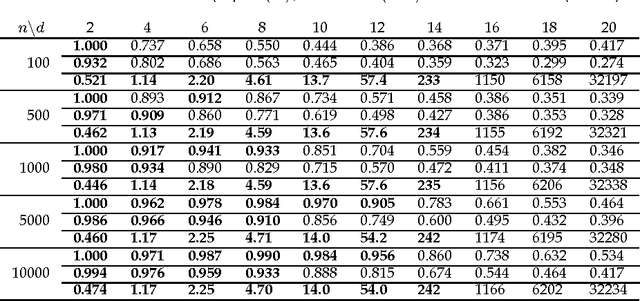
The notion of causality is used in many situations dealing with uncertainty. We consider the problem whether causality can be identified given data set generated by discrete random variables rather than continuous ones. In particular, for non-binary data, thus far it was only known that causality can be identified except rare cases. In this paper, we present necessary and sufficient condition for an integer modular acyclic additive noise (IMAN) of two variables. In addition, we relate bivariate and multivariate causal identifiability in a more explicit manner, and develop a practical algorithm to find the order of variables and their parent sets. We demonstrate its performance in applications to artificial data and real world body motion data with comparisons to conventional methods.

Discovering causal structures in binary exclusive-or skew acyclic models

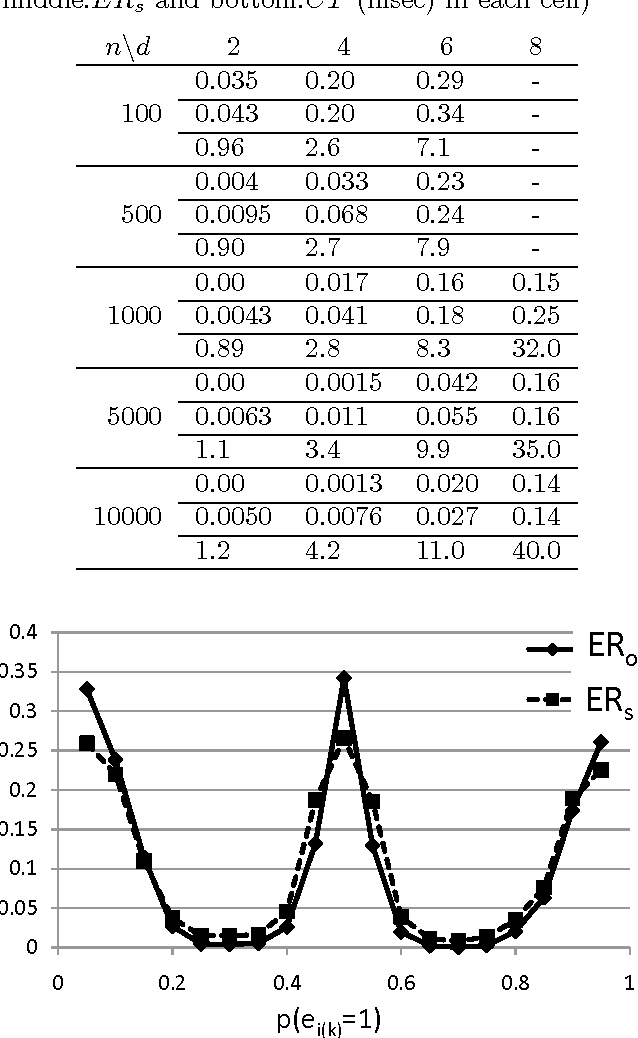
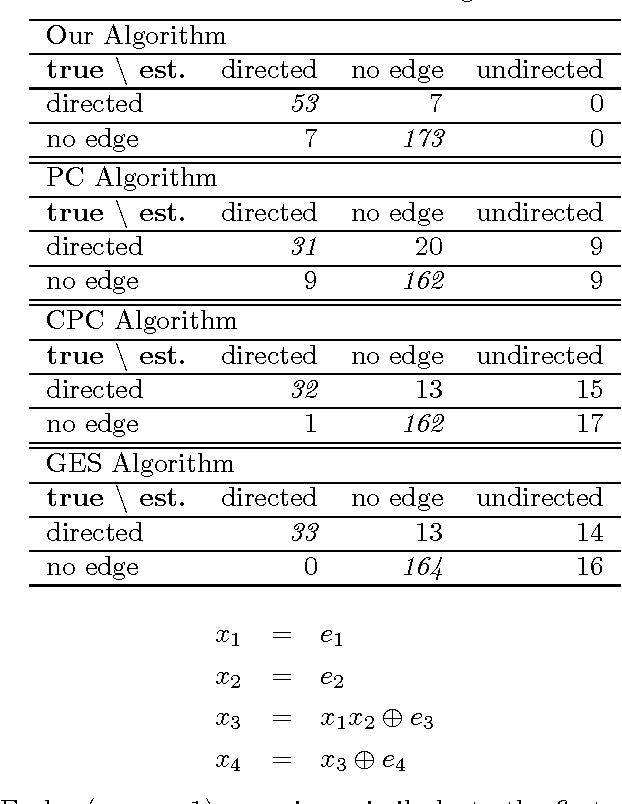
Discovering causal relations among observed variables in a given data set is a main topic in studies of statistics and artificial intelligence. Recently, some techniques to discover an identifiable causal structure have been explored based on non-Gaussianity of the observed data distribution. However, most of these are limited to continuous data. In this paper, we present a novel causal model for binary data and propose a new approach to derive an identifiable causal structure governing the data based on skew Bernoulli distributions of external noise. Experimental evaluation shows excellent performance for both artificial and real world data sets.

DirectLiNGAM: A direct method for learning a linear non-Gaussian structural equation model

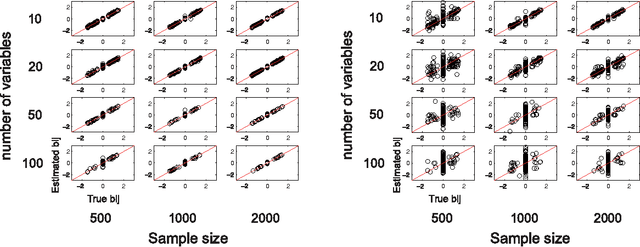
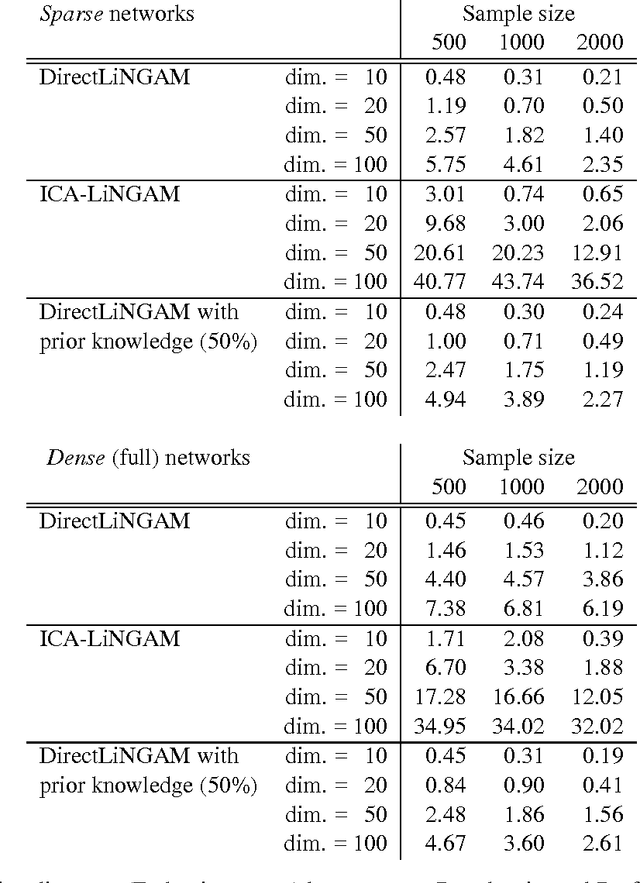
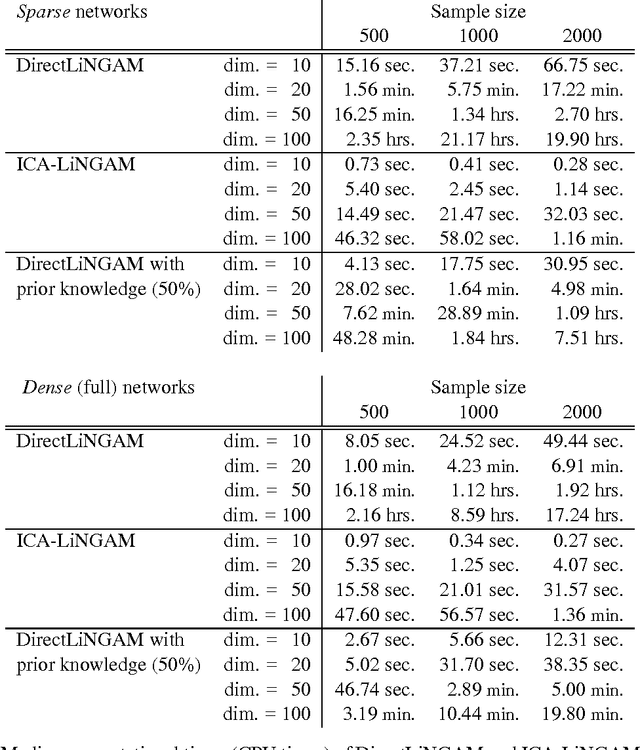
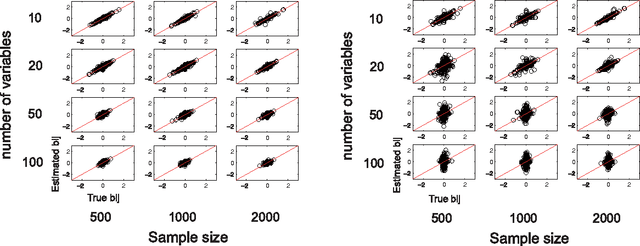
Structural equation models and Bayesian networks have been widely used to analyze causal relations between continuous variables. In such frameworks, linear acyclic models are typically used to model the data-generating process of variables. Recently, it was shown that use of non-Gaussianity identifies the full structure of a linear acyclic model, i.e., a causal ordering of variables and their connection strengths, without using any prior knowledge on the network structure, which is not the case with conventional methods. However, existing estimation methods are based on iterative search algorithms and may not converge to a correct solution in a finite number of steps. In this paper, we propose a new direct method to estimate a causal ordering and connection strengths based on non-Gaussianity. In contrast to the previous methods, our algorithm requires no algorithmic parameters and is guaranteed to converge to the right solution within a small fixed number of steps if the data strictly follows the model.