Bayesian estimation of possible causal direction in the presence of latent confounders using a linear non-Gaussian acyclic structural equation model with individual-specific effects

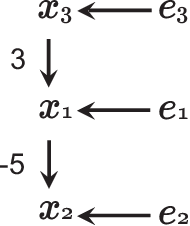
We consider learning the possible causal direction of two observed variables in the presence of latent confounding variables. Several existing methods have been shown to consistently estimate causal direction assuming linear or some type of nonlinear relationship and no latent confounders. However, the estimation results could be distorted if either assumption is actually violated. In this paper, we first propose a new linear non-Gaussian acyclic structural equation model with individual-specific effects that allows latent confounders to be considered. We then propose an empirical Bayesian approach for estimating possible causal direction using the new model. We demonstrate the effectiveness of our method using artificial and real-world data.

DirectLiNGAM: A direct method for learning a linear non-Gaussian structural equation model

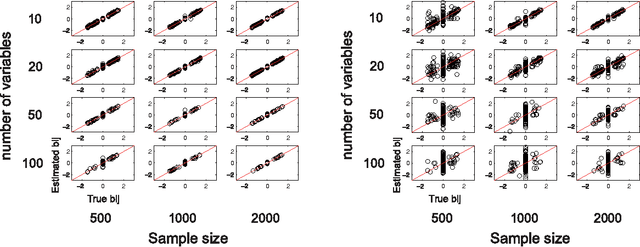
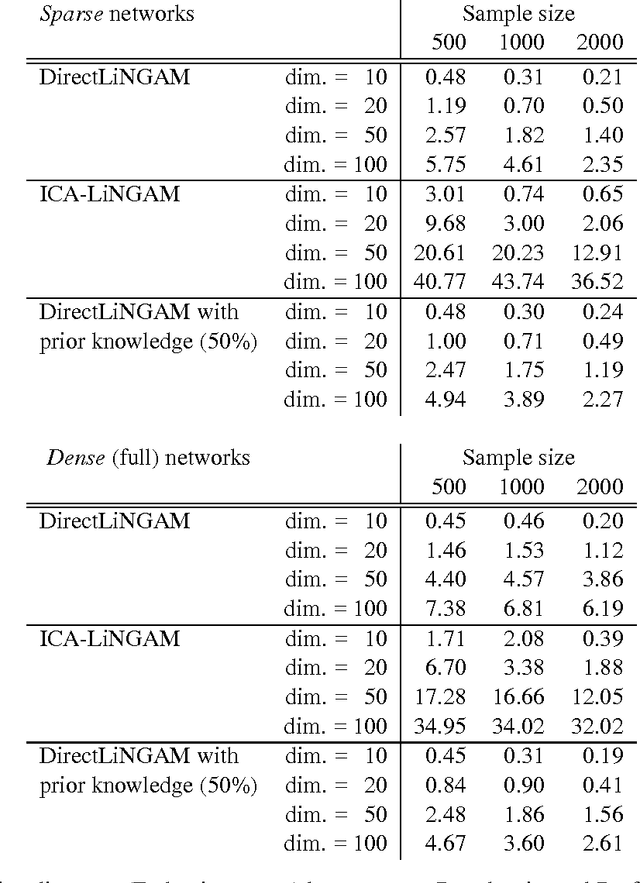
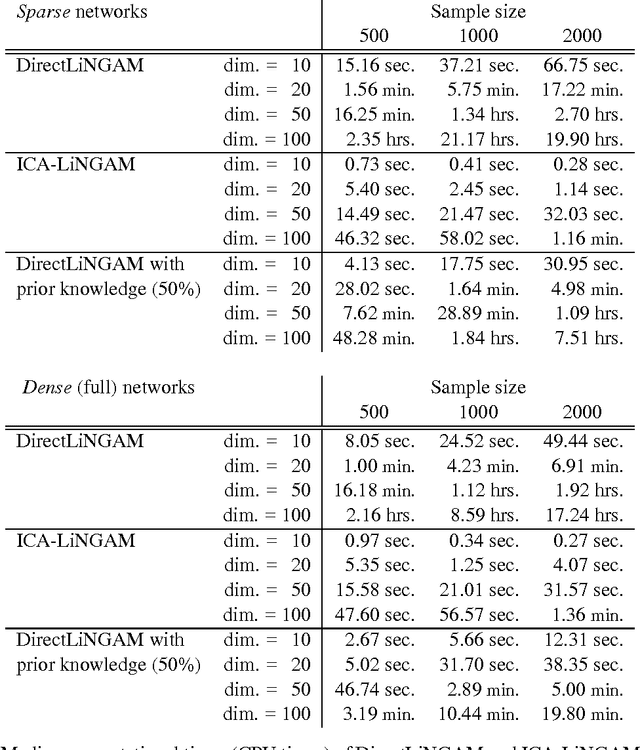
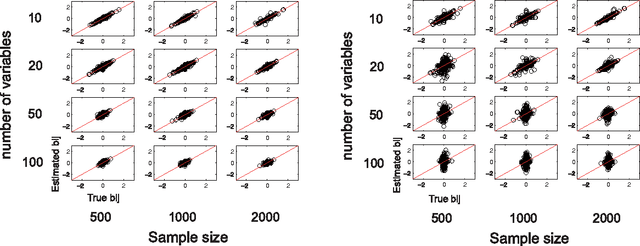
Structural equation models and Bayesian networks have been widely used to analyze causal relations between continuous variables. In such frameworks, linear acyclic models are typically used to model the data-generating process of variables. Recently, it was shown that use of non-Gaussianity identifies the full structure of a linear acyclic model, i.e., a causal ordering of variables and their connection strengths, without using any prior knowledge on the network structure, which is not the case with conventional methods. However, existing estimation methods are based on iterative search algorithms and may not converge to a correct solution in a finite number of steps. In this paper, we propose a new direct method to estimate a causal ordering and connection strengths based on non-Gaussianity. In contrast to the previous methods, our algorithm requires no algorithmic parameters and is guaranteed to converge to the right solution within a small fixed number of steps if the data strictly follows the model.

GroupLiNGAM: Linear non-Gaussian acyclic models for sets of variables

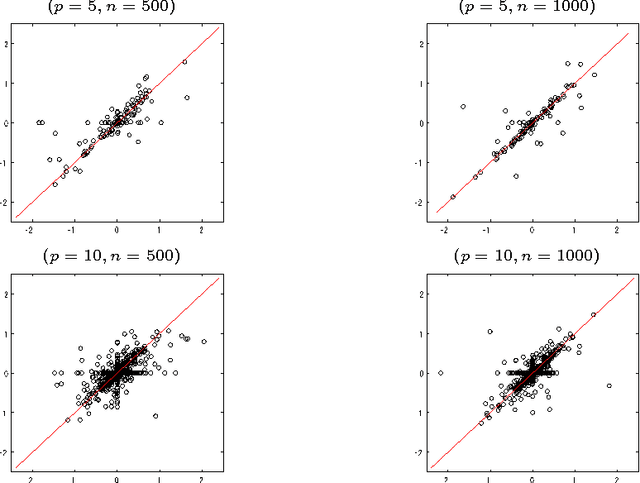
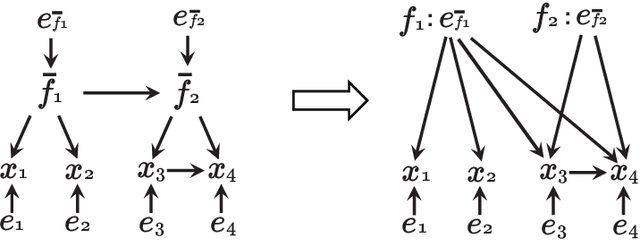
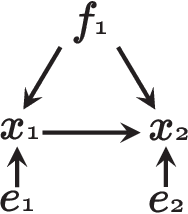
Finding the structure of a graphical model has been received much attention in many fields. Recently, it is reported that the non-Gaussianity of data enables us to identify the structure of a directed acyclic graph without any prior knowledge on the structure. In this paper, we propose a novel non-Gaussianity based algorithm for more general type of models; chain graphs. The algorithm finds an ordering of the disjoint subsets of variables by iteratively evaluating the independence between the variable subset and the residuals when the remaining variables are regressed on those. However, its computational cost grows exponentially according to the number of variables. Therefore, we further discuss an efficient approximate approach for applying the algorithm to large sized graphs. We illustrate the algorithm with artificial and real-world datasets.