Physics-inspired transformer quantum states via latent imaginary-time evolution

Neural quantum states (NQS) are powerful ansätze in the variational Monte Carlo framework, yet their architectures are often treated as black boxes. We propose a physically transparent framework in which NQS are treated as neural approximations to latent imaginary-time evolution. This viewpoint suggests that standard Transformer-based NQS (TQS) architectures correspond to physically unmotivated effective Hamiltonians dependent on imaginary time in a latent space. Building on this interpretation, we introduce physics-inspired transformer quantum states (PITQS), which enforce a static effective Hamiltonian by sharing weights across layers and improve propagation accuracy via Trotter-Suzuki decompositions without increasing the number of variational parameters. For the frustrated $J_1$-$J_2$ Heisenberg model, our ansätze achieve accuracies comparable to or exceeding state-of-the-art TQS while using substantially fewer variational parameters. This study demonstrates that reinterpreting the deep network structure as a latent cooling process enables a more physically grounded, systematic, and compact design, thereby bridging the gap between black-box expressivity and physically transparent construction.

Dualformer: Time-Frequency Dual Domain Learning for Long-term Time Series Forecasting

Transformer-based models, despite their promise for long-term time series forecasting (LTSF), suffer from an inherent low-pass filtering effect that limits their effectiveness. This issue arises due to undifferentiated propagation of frequency components across layers, causing a progressive attenuation of high-frequency information crucial for capturing fine-grained temporal variations. To address this limitation, we propose Dualformer, a principled dual-domain framework that rethinks frequency modeling from a layer-wise perspective. Dualformer introduces three key components: (1) a dual-branch architecture that concurrently models complementary temporal patterns in both time and frequency domains; (2) a hierarchical frequency sampling module that allocates distinct frequency bands to different layers, preserving high-frequency details in lower layers while modeling low-frequency trends in deeper layers; and (3) a periodicity-aware weighting mechanism that dynamically balances contributions from the dual branches based on the harmonic energy ratio of inputs, supported theoretically by a derived lower bound. This design enables structured frequency modeling and adaptive integration of time-frequency features, effectively preserving high-frequency information and enhancing generalization. Extensive experiments conducted on eight widely used benchmarks demonstrate Dualformer's robustness and superior performance, particularly on heterogeneous or weakly periodic data. Our code is publicly available at https://github.com/Akira-221/Dualformer.

Explorative Curriculum Learning for Strongly Correlated Electron Systems

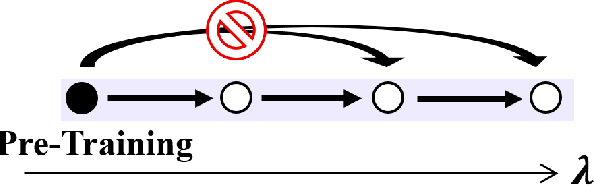
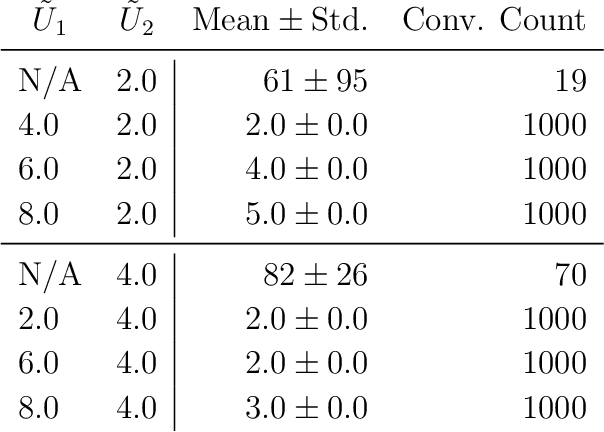
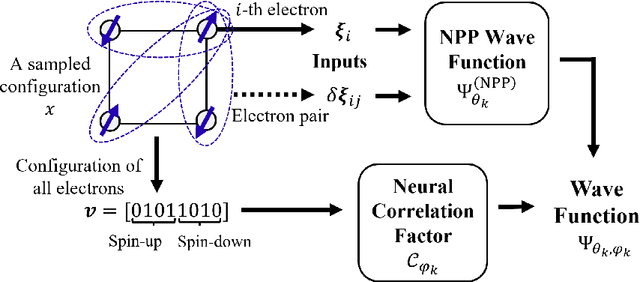
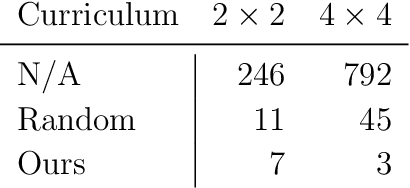
Recent advances in neural network quantum states (NQS) have enabled high-accuracy predictions for complex quantum many-body systems such as strongly correlated electron systems. However, the computational cost remains prohibitive, making exploration of the diverse parameters of interaction strengths and other physical parameters inefficient. While transfer learning has been proposed to mitigate this challenge, achieving generalization to large-scale systems and diverse parameter regimes remains difficult. To address this limitation, we propose a novel curriculum learning framework based on transfer learning for NQS. This facilitates efficient and stable exploration across a vast parameter space of quantum many-body systems. In addition, by interpreting NQS transfer learning through a perturbative lens, we demonstrate how prior physical knowledge can be flexibly incorporated into the curriculum learning process. We also propose Pairing-Net, an architecture to practically implement this strategy for strongly correlated electron systems, and empirically verify its effectiveness. Our results show an approximately 200-fold speedup in computation and a marked improvement in optimization stability compared to conventional methods.

Learning Stochastic Nonlinear Dynamics with Embedded Latent Transfer Operators

We consider an operator-based latent Markov representation of a stochastic nonlinear dynamical system, where the stochastic evolution of the latent state embedded in a reproducing kernel Hilbert space is described with the corresponding transfer operator, and develop a spectral method to learn this representation based on the theory of stochastic realization. The embedding may be learned simultaneously using reproducing kernels, for example, constructed with feed-forward neural networks. We also address the generalization of sequential state-estimation (Kalman filtering) in stochastic nonlinear systems, and of operator-based eigen-mode decomposition of dynamics, for the representation. Several examples with synthetic and real-world data are shown to illustrate the empirical characteristics of our methods, and to investigate the performance of our model in sequential state-estimation and mode decomposition.

Change-Point Detection in Industrial Data Streams based on Online Dynamic Mode Decomposition with Control

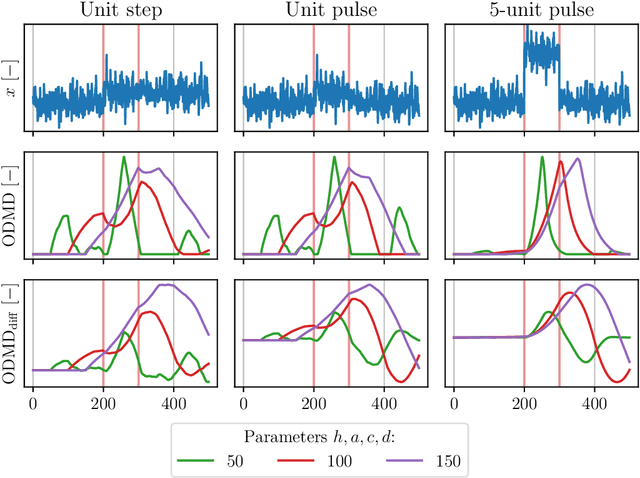
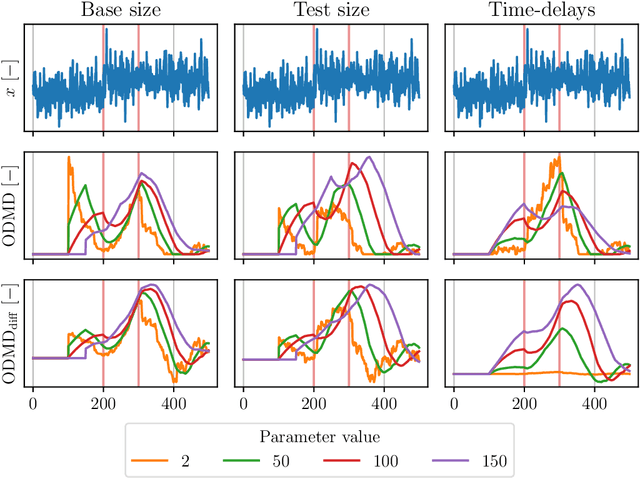
We propose a novel change-point detection method based on online Dynamic Mode Decomposition with control (ODMDwC). Leveraging ODMDwC's ability to find and track linear approximation of a non-linear system while incorporating control effects, the proposed method dynamically adapts to its changing behavior due to aging and seasonality. This approach enables the detection of changes in spatial, temporal, and spectral patterns, providing a robust solution that preserves correspondence between the score and the extent of change in the system dynamics. We formulate a truncated version of ODMDwC and utilize higher-order time-delay embeddings to mitigate noise and extract broad-band features. Our method addresses the challenges faced in industrial settings where safety-critical systems generate non-uniform data streams while requiring timely and accurate change-point detection to protect profit and life. Our results demonstrate that this method yields intuitive and improved detection results compared to the Singular-Value-Decomposition-based method. We validate our approach using synthetic and real-world data, showing its competitiveness to other approaches on complex systems' benchmark datasets. Provided guidelines for hyperparameters selection enhance our method's practical applicability.

SiT: Symmetry-Invariant Transformers for Generalisation in Reinforcement Learning

An open challenge in reinforcement learning (RL) is the effective deployment of a trained policy to new or slightly different situations as well as semantically-similar environments. We introduce Symmetry-Invariant Transformer (SiT), a scalable vision transformer (ViT) that leverages both local and global data patterns in a self-supervised manner to improve generalisation. Central to our approach is Graph Symmetric Attention, which refines the traditional self-attention mechanism to preserve graph symmetries, resulting in invariant and equivariant latent representations. We showcase SiT's superior generalization over ViTs on MiniGrid and Procgen RL benchmarks, and its sample efficiency on Atari 100k and CIFAR10.

The Disappearance of Timestep Embedding in Modern Time-Dependent Neural Networks

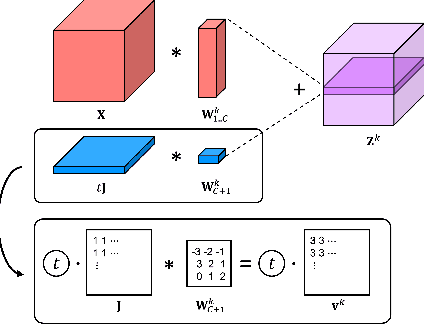
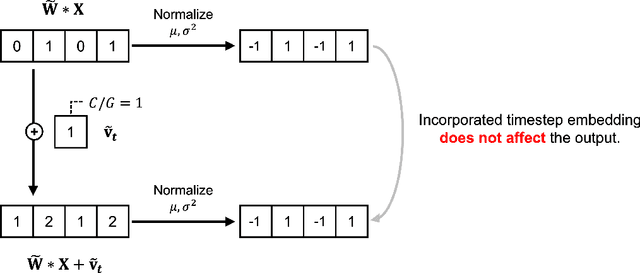
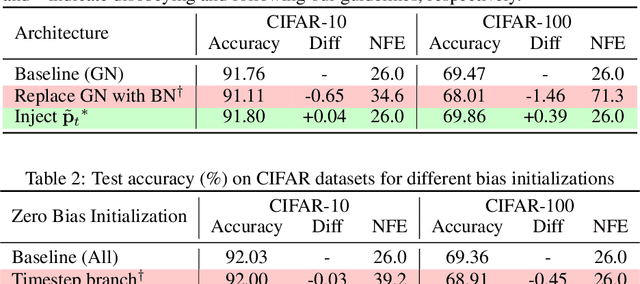
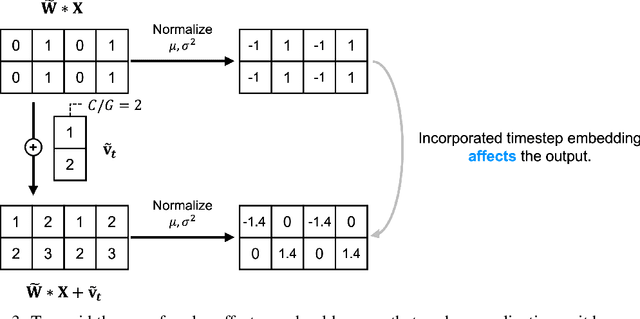
Dynamical systems are often time-varying, whose modeling requires a function that evolves with respect to time. Recent studies such as the neural ordinary differential equation proposed a time-dependent neural network, which provides a neural network varying with respect to time. However, we claim that the architectural choice to build a time-dependent neural network significantly affects its time-awareness but still lacks sufficient validation in its current states. In this study, we conduct an in-depth analysis of the architecture of modern time-dependent neural networks. Here, we report a vulnerability of vanishing timestep embedding, which disables the time-awareness of a time-dependent neural network. Furthermore, we find that this vulnerability can also be observed in diffusion models because they employ a similar architecture that incorporates timestep embedding to discriminate between different timesteps during a diffusion process. Our analysis provides a detailed description of this phenomenon as well as several solutions to address the root cause. Through experiments on neural ordinary differential equations and diffusion models, we observed that ensuring alive time-awareness via proposed solutions boosted their performance, which implies that their current implementations lack sufficient time-dependency.

Koopman operators with intrinsic observables in rigged reproducing kernel Hilbert spaces

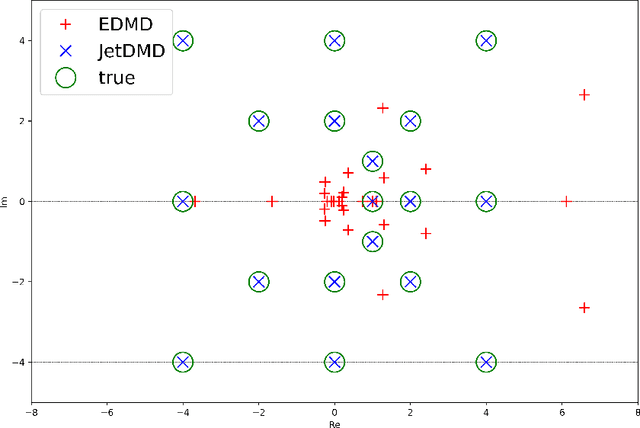
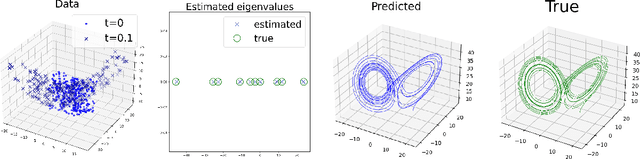
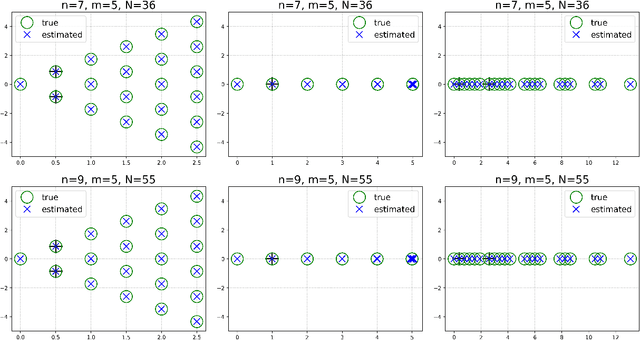
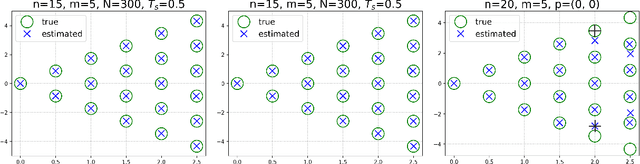
This paper presents a novel approach for estimating the Koopman operator defined on a reproducing kernel Hilbert space (RKHS) and its spectra. We propose an estimation method, what we call Jet Dynamic Mode Decomposition (JetDMD), leveraging the intrinsic structure of RKHS and the geometric notion known as jets to enhance the estimation of the Koopman operator. This method refines the traditional Extended Dynamic Mode Decomposition (EDMD) in accuracy, especially in the numerical estimation of eigenvalues. This paper proves JetDMD's superiority through explicit error bounds and convergence rate for special positive definite kernels, offering a solid theoretical foundation for its performance. We also delve into the spectral analysis of the Koopman operator, proposing the notion of extended Koopman operator within a framework of rigged Hilbert space. This notion leads to a deeper understanding of estimated Koopman eigenfunctions and capturing them outside the original function space. Through the theory of rigged Hilbert space, our study provides a principled methodology to analyze the estimated spectrum and eigenfunctions of Koopman operators, and enables eigendecomposition within a rigged RKHS. We also propose a new effective method for reconstructing the dynamical system from temporally-sampled trajectory data of the dynamical system with solid theoretical guarantee. We conduct several numerical simulations using the van der Pol oscillator, the Duffing oscillator, the H\'enon map, and the Lorenz attractor, and illustrate the performance of JetDMD with clear numerical computations of eigenvalues and accurate predictions of the dynamical systems.

Glocal Hypergradient Estimation with Koopman Operator

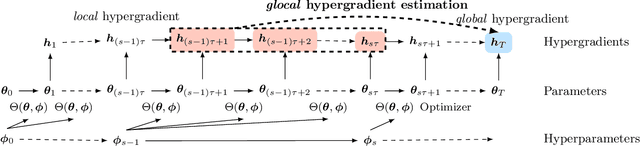
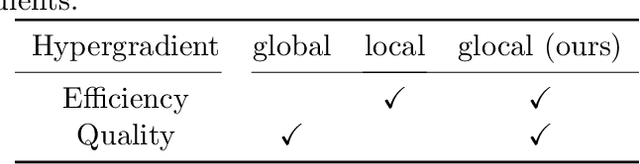
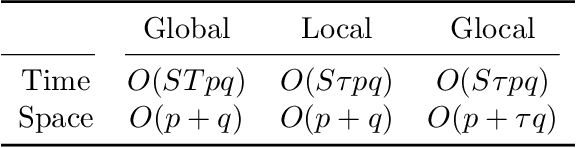
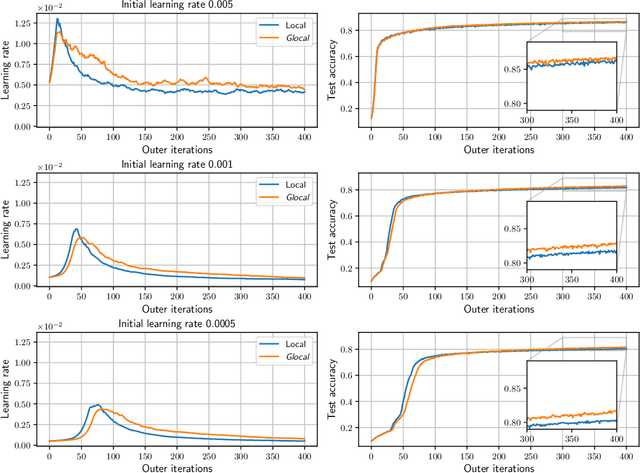
Gradient-based hyperparameter optimization methods update hyperparameters using hypergradients, gradients of a meta criterion with respect to hyperparameters. Previous research used two distinct update strategies: optimizing hyperparameters using global hypergradients obtained after completing model training or local hypergradients derived after every few model updates. While global hypergradients offer reliability, their computational cost is significant; conversely, local hypergradients provide speed but are often suboptimal. In this paper, we propose glocal hypergradient estimation, blending "global" quality with "local" efficiency. To this end, we use the Koopman operator theory to linearize the dynamics of hypergradients so that the global hypergradients can be efficiently approximated only by using a trajectory of local hypergradients. Consequently, we can optimize hyperparameters greedily using estimated global hypergradients, achieving both reliability and efficiency simultaneously. Through numerical experiments of hyperparameter optimization, including optimization of optimizers, we demonstrate the effectiveness of the glocal hypergradient estimation.

Fast, accurate, and interpretable decoding of electrocorticographic signals using dynamic mode decomposition

Dynamic mode (DM) decomposition decomposes spatiotemporal signals into basic oscillatory components (DMs). DMs can improve the accuracy of neural decoding when used with the nonlinear Grassmann kernel, compared to conventional power features. However, such kernel-based machine learning algorithms have three limitations: large computational time preventing real-time application, incompatibility with non-kernel algorithms, and low interpretability. Here, we propose a mapping function corresponding to the Grassmann kernel that explicitly transforms DMs into spatial DM (sDM) features, which can be used in any machine learning algorithm. Using electrocorticographic signals recorded during various movement and visual perception tasks, the sDM features were shown to improve the decoding accuracy and computational time compared to conventional methods. Furthermore, the components of the sDM features informative for decoding showed similar characteristics to the high-$\gamma$ power of the signals, but with higher trial-to-trial reproducibility. The proposed sDM features enable fast, accurate, and interpretable neural decoding.