Glocal Hypergradient Estimation with Koopman Operator
Paper and Code
Feb 05, 2024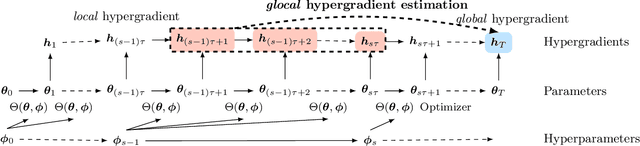
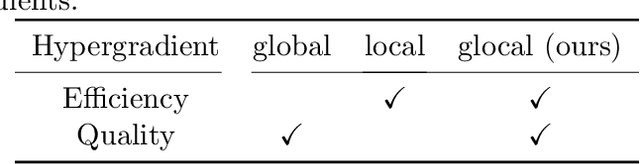
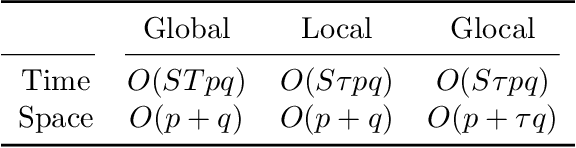
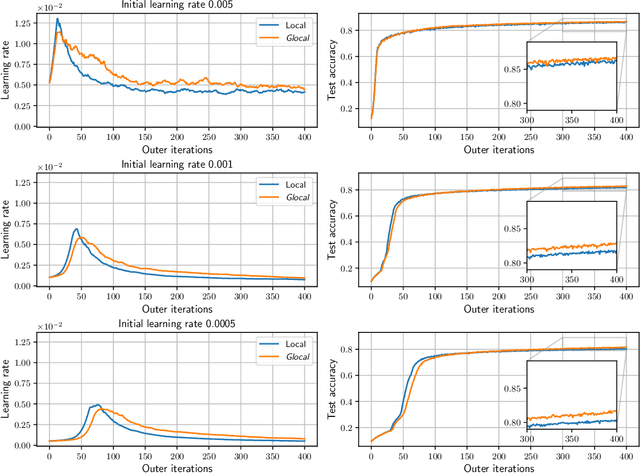
Gradient-based hyperparameter optimization methods update hyperparameters using hypergradients, gradients of a meta criterion with respect to hyperparameters. Previous research used two distinct update strategies: optimizing hyperparameters using global hypergradients obtained after completing model training or local hypergradients derived after every few model updates. While global hypergradients offer reliability, their computational cost is significant; conversely, local hypergradients provide speed but are often suboptimal. In this paper, we propose glocal hypergradient estimation, blending "global" quality with "local" efficiency. To this end, we use the Koopman operator theory to linearize the dynamics of hypergradients so that the global hypergradients can be efficiently approximated only by using a trajectory of local hypergradients. Consequently, we can optimize hyperparameters greedily using estimated global hypergradients, achieving both reliability and efficiency simultaneously. Through numerical experiments of hyperparameter optimization, including optimization of optimizers, we demonstrate the effectiveness of the glocal hypergradient estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge