Modeling Nonlinear Dynamics in Continuous Time with Inductive Biases on Decay Rates and/or Frequencies
Paper and Code
Dec 26, 2022
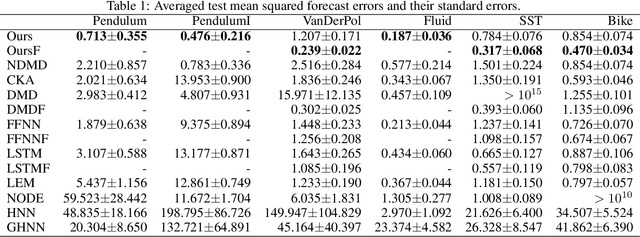
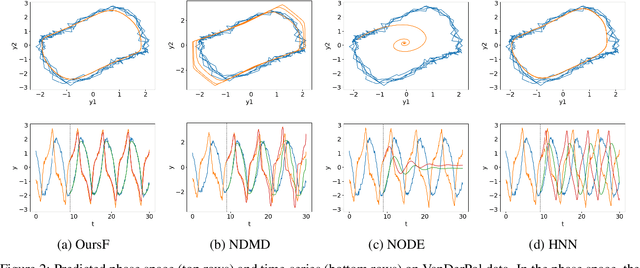

We propose a neural network-based model for nonlinear dynamics in continuous time that can impose inductive biases on decay rates and/or frequencies. Inductive biases are helpful for training neural networks especially when training data are small. The proposed model is based on the Koopman operator theory, where the decay rate and frequency information is used by restricting the eigenvalues of the Koopman operator that describe linear evolution in a Koopman space. We use neural networks to find an appropriate Koopman space, which are trained by minimizing multi-step forecasting and backcasting errors using irregularly sampled time-series data. Experiments on various time-series datasets demonstrate that the proposed method achieves higher forecasting performance given a single short training sequence than the existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge