Meta-learning Representations for Learning from Multiple Annotators

We propose a meta-learning method for learning from multiple noisy annotators. In many applications such as crowdsourcing services, labels for supervised learning are given by multiple annotators. Since the annotators have different skills or biases, given labels can be noisy. To learn accurate classifiers, existing methods require many noisy annotated data. However, sufficient data might be unavailable in practice. To overcome the lack of data, the proposed method uses labeled data obtained in different but related tasks. The proposed method embeds each example in tasks to a latent space by using a neural network and constructs a probabilistic model for learning a task-specific classifier while estimating annotators' abilities on the latent space. This neural network is meta-learned to improve the expected test classification performance when the classifier is adapted to a given small amount of annotated data. This classifier adaptation is performed by maximizing the posterior probability via the expectation-maximization (EM) algorithm. Since each step in the EM algorithm is easily computed as a closed-form and is differentiable, the proposed method can efficiently backpropagate the loss through the EM algorithm to meta-learn the neural network. We show the effectiveness of our method with real-world datasets with synthetic noise and real-world crowdsourcing datasets.

K$^2$IE: Kernel Method-based Kernel Intensity Estimators for Inhomogeneous Poisson Processes

Kernel method-based intensity estimators, formulated within reproducing kernel Hilbert spaces (RKHSs), and classical kernel intensity estimators (KIEs) have been among the most easy-to-implement and feasible methods for estimating the intensity functions of inhomogeneous Poisson processes. While both approaches share the term "kernel", they are founded on distinct theoretical principles, each with its own strengths and limitations. In this paper, we propose a novel regularized kernel method for Poisson processes based on the least squares loss and show that the resulting intensity estimator involves a specialized variant of the representer theorem: it has the dual coefficient of unity and coincides with classical KIEs. This result provides new theoretical insights into the connection between classical KIEs and kernel method-based intensity estimators, while enabling us to develop an efficient KIE by leveraging advanced techniques from RKHS theory. We refer to the proposed model as the kernel method-based kernel intensity estimator (K$^2$IE). Through experiments on synthetic datasets, we show that K$^2$IE achieves comparable predictive performance while significantly surpassing the state-of-the-art kernel method-based estimator in computational efficiency.

Positive-Unlabeled Diffusion Models for Preventing Sensitive Data Generation

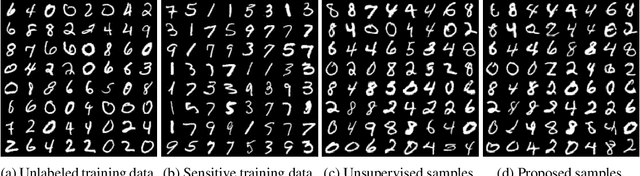
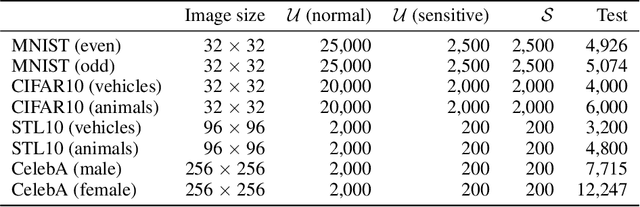
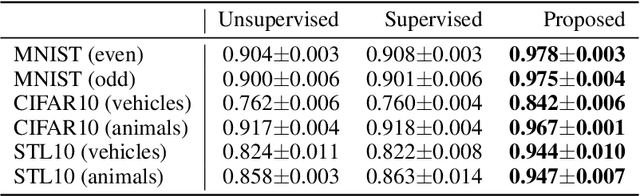
Diffusion models are powerful generative models but often generate sensitive data that are unwanted by users, mainly because the unlabeled training data frequently contain such sensitive data. Since labeling all sensitive data in the large-scale unlabeled training data is impractical, we address this problem by using a small amount of labeled sensitive data. In this paper, we propose positive-unlabeled diffusion models, which prevent the generation of sensitive data using unlabeled and sensitive data. Our approach can approximate the evidence lower bound (ELBO) for normal (negative) data using only unlabeled and sensitive (positive) data. Therefore, even without labeled normal data, we can maximize the ELBO for normal data and minimize it for labeled sensitive data, ensuring the generation of only normal data. Through experiments across various datasets and settings, we demonstrated that our approach can prevent the generation of sensitive images without compromising image quality.

Deep Koopman-layered Model with Universal Property Based on Toeplitz Matrices

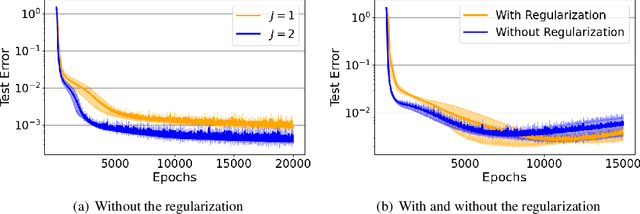
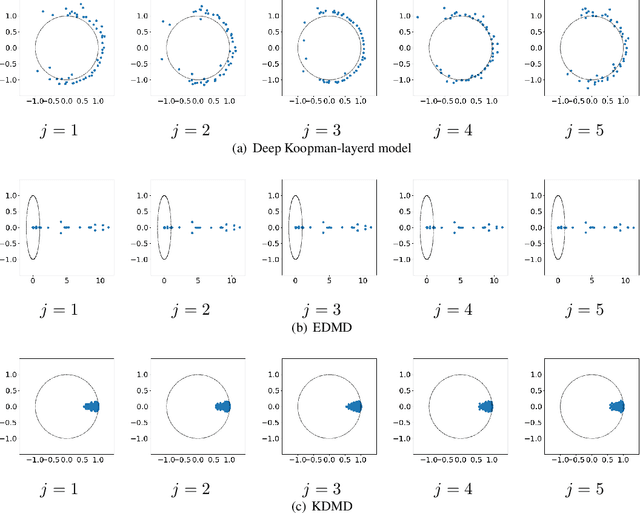
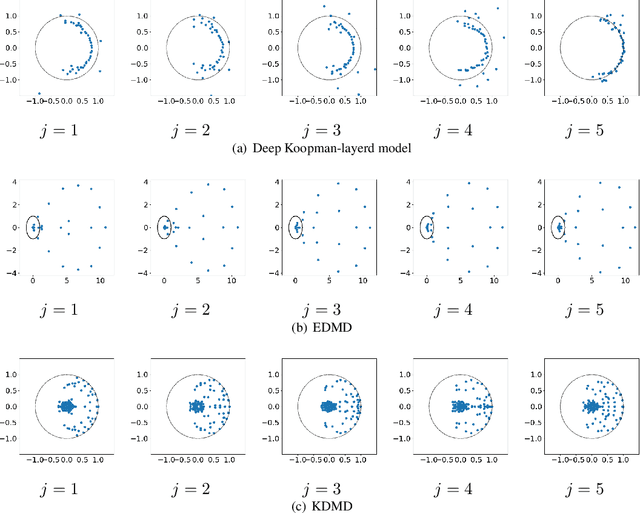
We propose deep Koopman-layered models with learnable parameters in the form of Toeplitz matrices for analyzing the dynamics of time-series data. The proposed model has both theoretical solidness and flexibility. By virtue of the universal property of Toeplitz matrices and the reproducing property underlined in the model, we can show its universality and the generalization property. In addition, the flexibility of the proposed model enables the model to fit time-series data coming from nonautonomous dynamical systems. When training the model, we apply Krylov subspace methods for efficient computations. In addition, the proposed model can be regarded as a neural ODE-based model. In this sense, the proposed model establishes a new connection among Koopman operators, neural ODEs, and numerical linear algebraic methods.

Meta-learning for Positive-unlabeled Classification

We propose a meta-learning method for positive and unlabeled (PU) classification, which improves the performance of binary classifiers obtained from only PU data in unseen target tasks. PU learning is an important problem since PU data naturally arise in real-world applications such as outlier detection and information retrieval. Existing PU learning methods require many PU data, but sufficient data are often unavailable in practice. The proposed method minimizes the test classification risk after the model is adapted to PU data by using related tasks that consist of positive, negative, and unlabeled data. We formulate the adaptation as an estimation problem of the Bayes optimal classifier, which is an optimal classifier to minimize the classification risk. The proposed method embeds each instance into a task-specific space using neural networks. With the embedded PU data, the Bayes optimal classifier is estimated through density-ratio estimation of PU densities, whose solution is obtained as a closed-form solution. The closed-form solution enables us to efficiently and effectively minimize the test classification risk. We empirically show that the proposed method outperforms existing methods with one synthetic and three real-world datasets.

Deep Positive-Unlabeled Anomaly Detection for Contaminated Unlabeled Data

Semi-supervised anomaly detection, which aims to improve the performance of the anomaly detector by using a small amount of anomaly data in addition to unlabeled data, has attracted attention. Existing semi-supervised approaches assume that unlabeled data are mostly normal. They train the anomaly detector to minimize the anomaly scores for the unlabeled data, and to maximize those for the anomaly data. However, in practice, the unlabeled data are often contaminated with anomalies. This weakens the effect of maximizing the anomaly scores for anomalies, and prevents us from improving the detection performance. To solve this problem, we propose the positive-unlabeled autoencoder, which is based on positive-unlabeled learning and the anomaly detector such as the autoencoder. With our approach, we can approximate the anomaly scores for normal data using the unlabeled and anomaly data. Therefore, without the labeled normal data, we can train the anomaly detector to minimize the anomaly scores for normal data, and to maximize those for the anomaly data. In addition, our approach is applicable to various anomaly detectors such as the DeepSVDD. Experiments on various datasets show that our approach achieves better detection performance than existing approaches.

Neural Operators Meet Energy-based Theory: Operator Learning for Hamiltonian and Dissipative PDEs

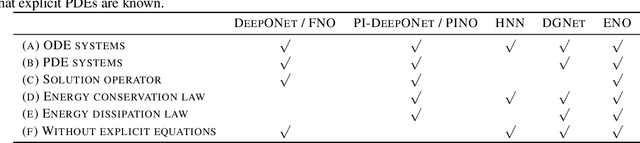
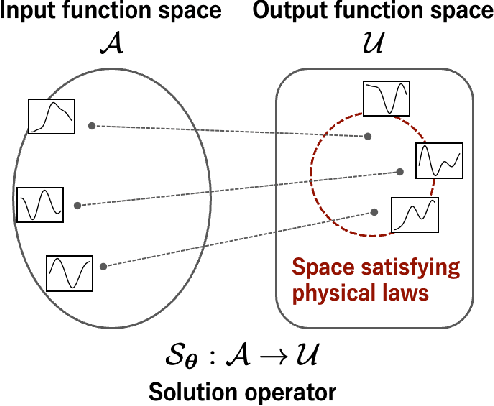
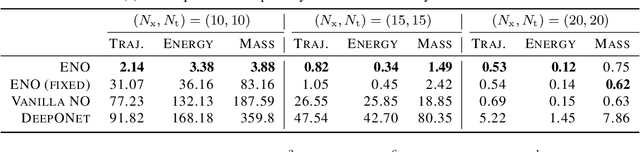
The operator learning has received significant attention in recent years, with the aim of learning a mapping between function spaces. Prior works have proposed deep neural networks (DNNs) for learning such a mapping, enabling the learning of solution operators of partial differential equations (PDEs). However, these works still struggle to learn dynamics that obeys the laws of physics. This paper proposes Energy-consistent Neural Operators (ENOs), a general framework for learning solution operators of PDEs that follows the energy conservation or dissipation law from observed solution trajectories. We introduce a novel penalty function inspired by the energy-based theory of physics for training, in which the energy functional is modeled by another DNN, allowing one to bias the outputs of the DNN-based solution operators to ensure energetic consistency without explicit PDEs. Experiments on multiple physical systems show that ENO outperforms existing DNN models in predicting solutions from data, especially in super-resolution settings.

Meta-Learning for Neural Network-based Temporal Point Processes

Human activities generate various event sequences such as taxi trip records, bike-sharing pick-ups, crime occurrence, and infectious disease transmission. The point process is widely used in many applications to predict such events related to human activities. However, point processes present two problems in predicting events related to human activities. First, recent high-performance point process models require the input of sufficient numbers of events collected over a long period (i.e., long sequences) for training, which are often unavailable in realistic situations. Second, the long-term predictions required in real-world applications are difficult. To tackle these problems, we propose a novel meta-learning approach for periodicity-aware prediction of future events given short sequences. The proposed method first embeds short sequences into hidden representations (i.e., task representations) via recurrent neural networks for creating predictions from short sequences. It then models the intensity of the point process by monotonic neural networks (MNNs), with the input being the task representations. We transfer the prior knowledge learned from related tasks and can improve event prediction given short sequences of target tasks. We design the MNNs to explicitly take temporal periodic patterns into account, contributing to improved long-term prediction performance. Experiments on multiple real-world datasets demonstrate that the proposed method has higher prediction performance than existing alternatives.

Meta-learning to Calibrate Gaussian Processes with Deep Kernels for Regression Uncertainty Estimation

Although Gaussian processes (GPs) with deep kernels have been successfully used for meta-learning in regression tasks, its uncertainty estimation performance can be poor. We propose a meta-learning method for calibrating deep kernel GPs for improving regression uncertainty estimation performance with a limited number of training data. The proposed method meta-learns how to calibrate uncertainty using data from various tasks by minimizing the test expected calibration error, and uses the knowledge for unseen tasks. We design our model such that the adaptation and calibration for each task can be performed without iterative procedures, which enables effective meta-learning. In particular, a task-specific uncalibrated output distribution is modeled by a GP with a task-shared encoder network, and it is transformed to a calibrated one using a cumulative density function of a task-specific Gaussian mixture model (GMM). By integrating the GP and GMM into our neural network-based model, we can meta-learn model parameters in an end-to-end fashion. Our experiments demonstrate that the proposed method improves uncertainty estimation performance while keeping high regression performance compared with the existing methods using real-world datasets in few-shot settings.

Meta-learning of semi-supervised learning from tasks with heterogeneous attribute spaces

We propose a meta-learning method for semi-supervised learning that learns from multiple tasks with heterogeneous attribute spaces. The existing semi-supervised meta-learning methods assume that all tasks share the same attribute space, which prevents us from learning with a wide variety of tasks. With the proposed method, the expected test performance on tasks with a small amount of labeled data is improved with unlabeled data as well as data in various tasks, where the attribute spaces are different among tasks. The proposed method embeds labeled and unlabeled data simultaneously in a task-specific space using a neural network, and the unlabeled data's labels are estimated by adapting classification or regression models in the embedding space. For the neural network, we develop variable-feature self-attention layers, which enable us to find embeddings of data with different attribute spaces with a single neural network by considering interactions among examples, attributes, and labels. Our experiments on classification and regression datasets with heterogeneous attribute spaces demonstrate that our proposed method outperforms the existing meta-learning and semi-supervised learning methods.