Meta-Learning for Neural Network-based Temporal Point Processes

Human activities generate various event sequences such as taxi trip records, bike-sharing pick-ups, crime occurrence, and infectious disease transmission. The point process is widely used in many applications to predict such events related to human activities. However, point processes present two problems in predicting events related to human activities. First, recent high-performance point process models require the input of sufficient numbers of events collected over a long period (i.e., long sequences) for training, which are often unavailable in realistic situations. Second, the long-term predictions required in real-world applications are difficult. To tackle these problems, we propose a novel meta-learning approach for periodicity-aware prediction of future events given short sequences. The proposed method first embeds short sequences into hidden representations (i.e., task representations) via recurrent neural networks for creating predictions from short sequences. It then models the intensity of the point process by monotonic neural networks (MNNs), with the input being the task representations. We transfer the prior knowledge learned from related tasks and can improve event prediction given short sequences of target tasks. We design the MNNs to explicitly take temporal periodic patterns into account, contributing to improved long-term prediction performance. Experiments on multiple real-world datasets demonstrate that the proposed method has higher prediction performance than existing alternatives.

Aggregated Multi-output Gaussian Processes with Knowledge Transfer Across Domains

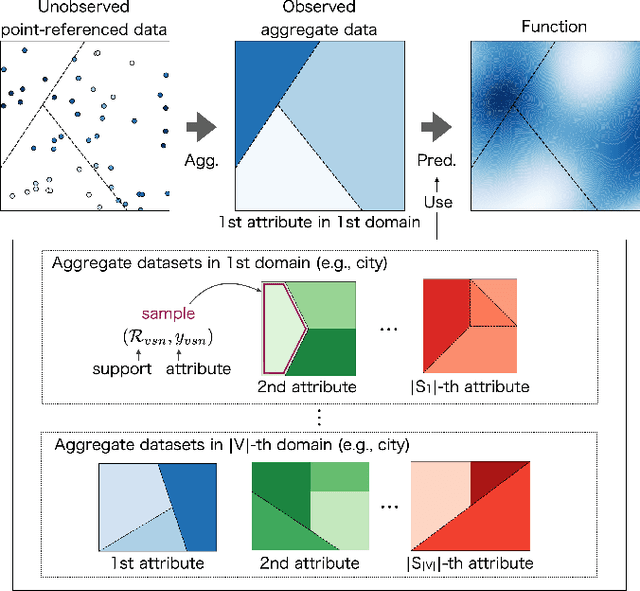
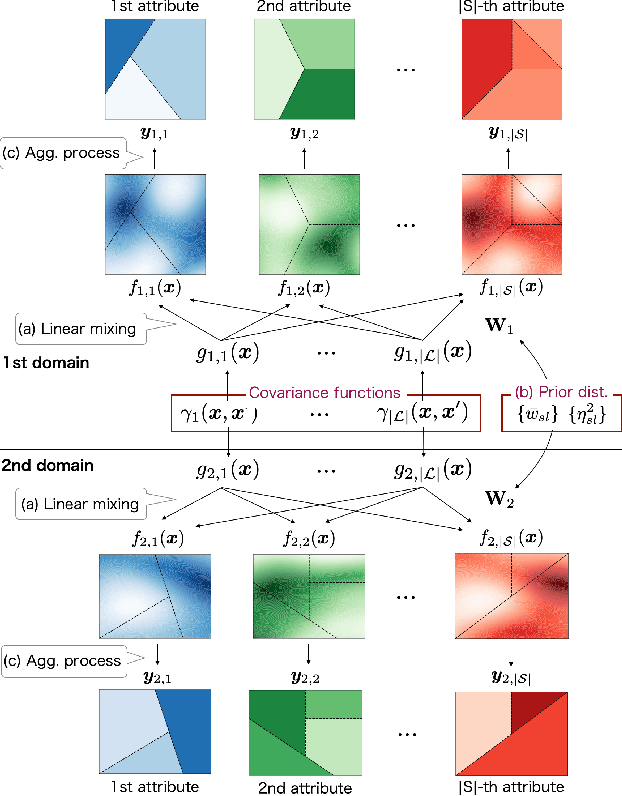
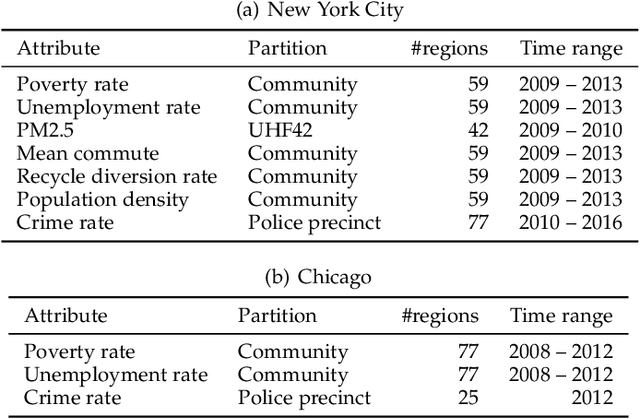
Aggregate data often appear in various fields such as socio-economics and public security. The aggregate data are associated not with points but with supports (e.g., spatial regions in a city). Since the supports may have various granularities depending on attributes (e.g., poverty rate and crime rate), modeling such data is not straightforward. This article offers a multi-output Gaussian process (MoGP) model that infers functions for attributes using multiple aggregate datasets of respective granularities. In the proposed model, the function for each attribute is assumed to be a dependent GP modeled as a linear mixing of independent latent GPs. We design an observation model with an aggregation process for each attribute; the process is an integral of the GP over the corresponding support. We also introduce a prior distribution of the mixing weights, which allows a knowledge transfer across domains (e.g., cities) by sharing the prior. This is advantageous in such a situation where the spatially aggregated dataset in a city is too coarse to interpolate; the proposed model can still make accurate predictions of attributes by utilizing aggregate datasets in other cities. The inference of the proposed model is based on variational Bayes, which enables one to learn the model parameters using the aggregate datasets from multiple domains. The experiments demonstrate that the proposed model outperforms in the task of refining coarse-grained aggregate data on real-world datasets: Time series of air pollutants in Beijing and various kinds of spatial datasets from New York City and Chicago.

Dynamic Hawkes Processes for Discovering Time-evolving Communities' States behind Diffusion Processes

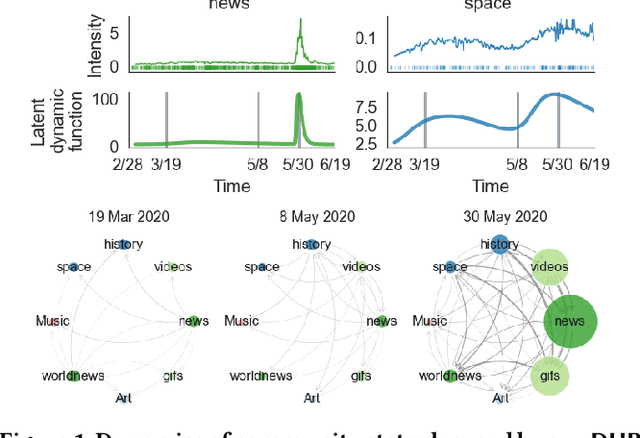
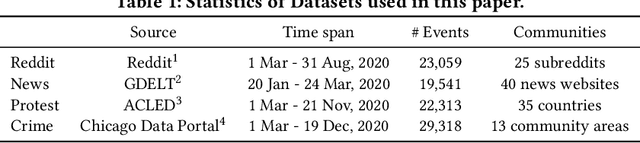
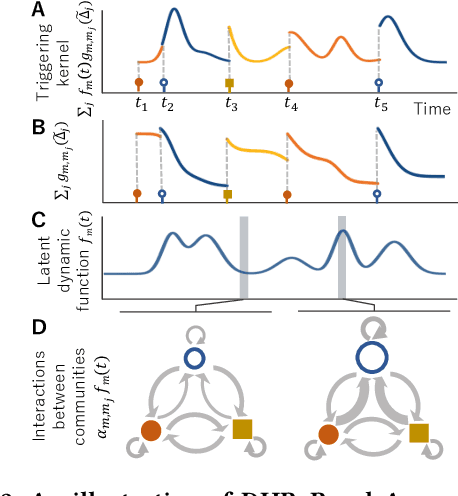
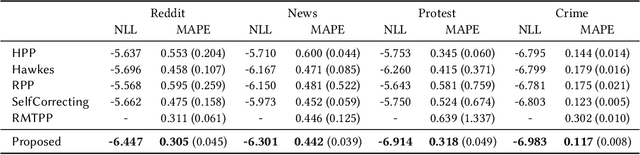
Sequences of events including infectious disease outbreaks, social network activities, and crimes are ubiquitous and the data on such events carry essential information about the underlying diffusion processes between communities (e.g., regions, online user groups). Modeling diffusion processes and predicting future events are crucial in many applications including epidemic control, viral marketing, and predictive policing. Hawkes processes offer a central tool for modeling the diffusion processes, in which the influence from the past events is described by the triggering kernel. However, the triggering kernel parameters, which govern how each community is influenced by the past events, are assumed to be static over time. In the real world, the diffusion processes depend not only on the influences from the past, but also the current (time-evolving) states of the communities, e.g., people's awareness of the disease and people's current interests. In this paper, we propose a novel Hawkes process model that is able to capture the underlying dynamics of community states behind the diffusion processes and predict the occurrences of events based on the dynamics. Specifically, we model the latent dynamic function that encodes these hidden dynamics by a mixture of neural networks. Then we design the triggering kernel using the latent dynamic function and its integral. The proposed method, termed DHP (Dynamic Hawkes Processes), offers a flexible way to learn complex representations of the time-evolving communities' states, while at the same time it allows to computing the exact likelihood, which makes parameter learning tractable. Extensive experiments on four real-world event datasets show that DHP outperforms five widely adopted methods for event prediction.

Non-approximate Inference for Collective Graphical Models on Path Graphs via Discrete Difference of Convex Algorithm

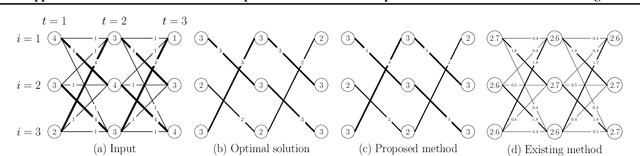
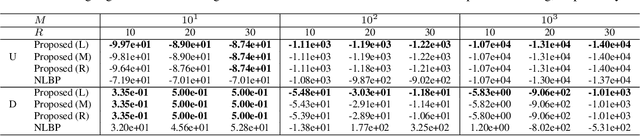
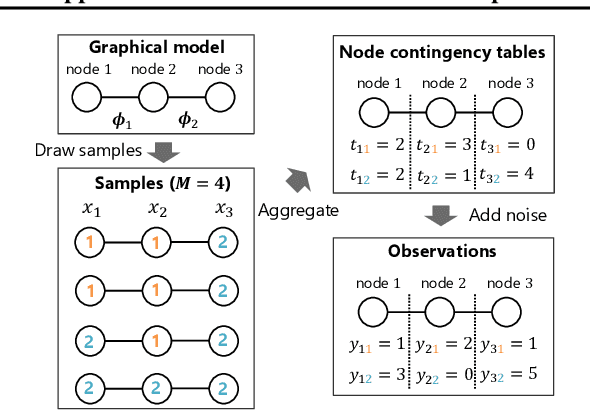
The importance of aggregated count data, which is calculated from the data of multiple individuals, continues to increase. Collective Graphical Model (CGM) is a probabilistic approach to the analysis of aggregated data. One of the most important operations in CGM is maximum a posteriori (MAP) inference of unobserved variables under given observations. Because the MAP inference problem for general CGMs has been shown to be NP-hard, an approach that solves an approximate problem has been proposed. However, this approach has two major drawbacks. First, the quality of the solution deteriorates when the values in the count tables are small, because the approximation becomes inaccurate. Second, since continuous relaxation is applied, the integrality constraints of the output are violated. To resolve these problems, this paper proposes a new method for MAP inference for CGMs on path graphs. First we show that the MAP inference problem can be formulated as a (non-linear) minimum cost flow problem. Then, we apply Difference of Convex Algorithm (DCA), which is a general methodology to minimize a function represented as the sum of a convex function and a concave function. In our algorithm, important subroutines in DCA can be efficiently calculated by minimum convex cost flow algorithms. Experiments show that the proposed method outputs higher quality solutions than the conventional approach.

Probabilistic Optimal Transport based on Collective Graphical Models

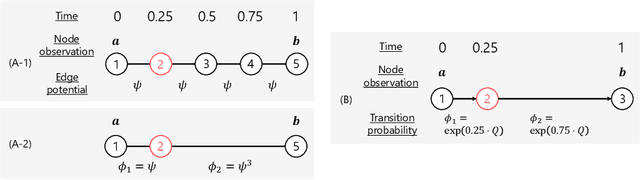
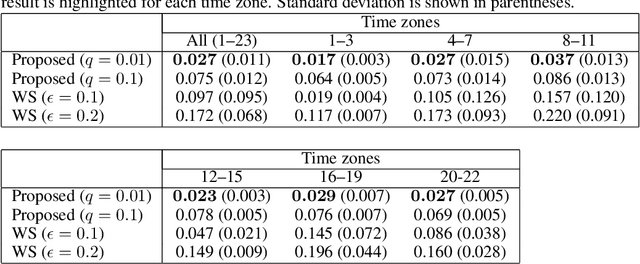
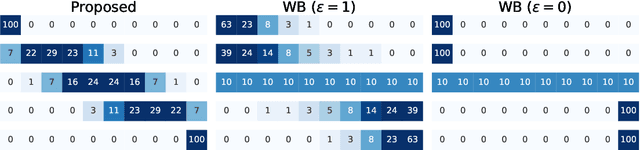
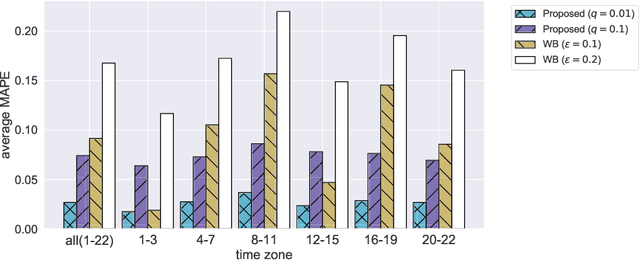
Optimal Transport (OT) is being widely used in various fields such as machine learning and computer vision, as it is a powerful tool for measuring the similarity between probability distributions and histograms. In previous studies, OT has been defined as the minimum cost to transport probability mass from one probability distribution to another. In this study, we propose a new framework in which OT is considered as a maximum a posteriori (MAP) solution of a probabilistic generative model. With the proposed framework, we show that OT with entropic regularization is equivalent to maximizing a posterior probability of a probabilistic model called Collective Graphical Model (CGM), which describes aggregated statistics of multiple samples generated from a graphical model. Interpreting OT as a MAP solution of a CGM has the following two advantages: (i) We can calculate the discrepancy between noisy histograms by modeling noise distributions. Since various distributions can be used for noise modeling, it is possible to select the noise distribution flexibly to suit the situation. (ii) We can construct a new method for interpolation between histograms, which is an important application of OT. The proposed method allows for intuitive modeling based on the probabilistic interpretations, and a simple and efficient estimation algorithm is available. Experiments using synthetic and real-world spatio-temporal population datasets show the effectiveness of the proposed interpolation method.

Spatially Aggregated Gaussian Processes with Multivariate Areal Outputs

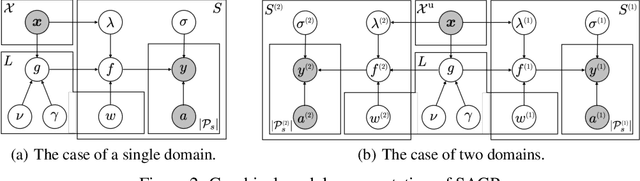
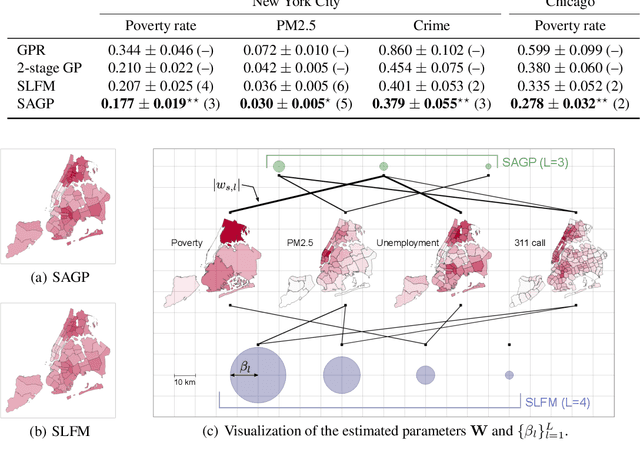
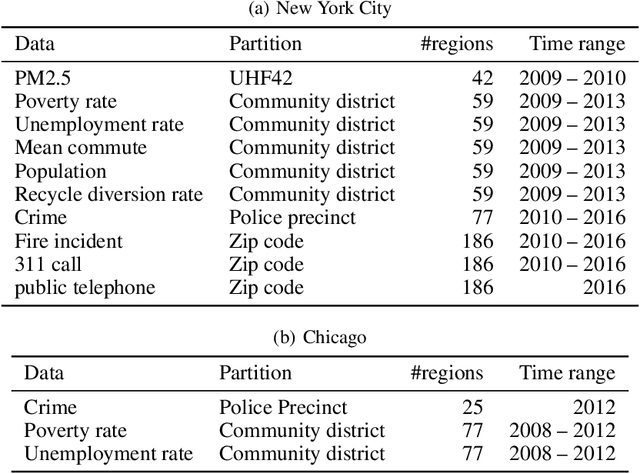
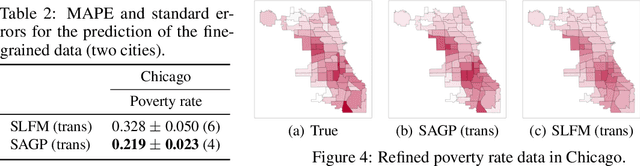
We propose a probabilistic model for inferring the multivariate function from multiple areal data sets with various granularities. Here, the areal data are observed not at location points but at regions. Existing regression-based models require the fine-grained auxiliary data sets on the same domain. With the proposed model, the functions for respective areal data sets are assumed to be a multivariate dependent Gaussian process (GP) that is modeled as a linear mixing of independent latent GPs. Sharing of latent GPs across multiple areal data sets allows us to effectively estimate spatial correlation for each areal data set; moreover it can easily be extended to transfer learning across multiple domains. To handle the multivariate areal data, we design its observation model with a spatial aggregation process for each areal data set, which is an integral of the mixed GP over the corresponding region. By deriving the posterior GP, we can predict the data value at any location point by considering the spatial correlations and the dependences between areal data sets simultaneously. Our experiments on real-world data sets demonstrate that our model can 1) accurately refine the coarse-grained areal data, and 2) offer performance improvements by using the areal data sets from multiple domains.

Deep Mixture Point Processes: Spatio-temporal Event Prediction with Rich Contextual Information

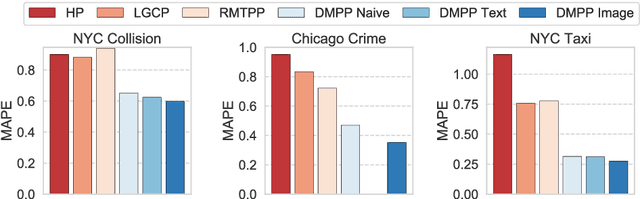
Predicting when and where events will occur in cities, like taxi pick-ups, crimes, and vehicle collisions, is a challenging and important problem with many applications in fields such as urban planning, transportation optimization and location-based marketing. Though many point processes have been proposed to model events in a continuous spatio-temporal space, none of them allow for the consideration of the rich contextual factors that affect event occurrence, such as weather, social activities, geographical characteristics, and traffic. In this paper, we propose \textsf{DMPP} (Deep Mixture Point Processes), a point process model for predicting spatio-temporal events with the use of rich contextual information; a key advance is its incorporation of the heterogeneous and high-dimensional context available in image and text data. Specifically, we design the intensity of our point process model as a mixture of kernels, where the mixture weights are modeled by a deep neural network. This formulation allows us to automatically learn the complex nonlinear effects of the contextual factors on event occurrence. At the same time, this formulation makes analytical integration over the intensity, which is required for point process estimation, tractable. We use real-world data sets from different domains to demonstrate that DMPP has better predictive performance than existing methods.

Refining Coarse-grained Spatial Data using Auxiliary Spatial Data Sets with Various Granularities

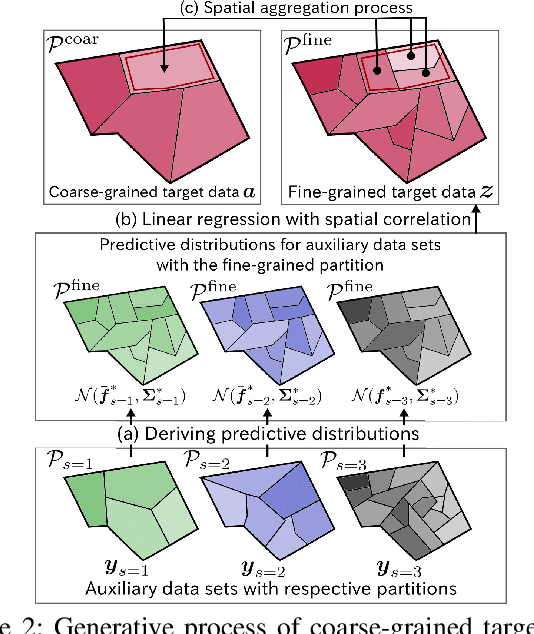
We propose a probabilistic model for refining coarse-grained spatial data by utilizing auxiliary spatial data sets. Existing methods require that the spatial granularities of the auxiliary data sets are the same as the desired granularity of target data. The proposed model can effectively make use of auxiliary data sets with various granularities by hierarchically incorporating Gaussian processes. With the proposed model, a distribution for each auxiliary data set on the continuous space is modeled using a Gaussian process, where the representation of uncertainty considers the levels of granularity. The fine-grained target data are modeled by another Gaussian process that considers both the spatial correlation and the auxiliary data sets with their uncertainty. We integrate the Gaussian process with a spatial aggregation process that transforms the fine-grained target data into the coarse-grained target data, by which we can infer the fine-grained target Gaussian process from the coarse-grained data. Our model is designed such that the inference of model parameters based on the exact marginal likelihood is possible, in which the variables of fine-grained target and auxiliary data are analytically integrated out. Our experiments on real-world spatial data sets demonstrate the effectiveness of the proposed model.