Meta-Learning for Neural Network-based Temporal Point Processes

Human activities generate various event sequences such as taxi trip records, bike-sharing pick-ups, crime occurrence, and infectious disease transmission. The point process is widely used in many applications to predict such events related to human activities. However, point processes present two problems in predicting events related to human activities. First, recent high-performance point process models require the input of sufficient numbers of events collected over a long period (i.e., long sequences) for training, which are often unavailable in realistic situations. Second, the long-term predictions required in real-world applications are difficult. To tackle these problems, we propose a novel meta-learning approach for periodicity-aware prediction of future events given short sequences. The proposed method first embeds short sequences into hidden representations (i.e., task representations) via recurrent neural networks for creating predictions from short sequences. It then models the intensity of the point process by monotonic neural networks (MNNs), with the input being the task representations. We transfer the prior knowledge learned from related tasks and can improve event prediction given short sequences of target tasks. We design the MNNs to explicitly take temporal periodic patterns into account, contributing to improved long-term prediction performance. Experiments on multiple real-world datasets demonstrate that the proposed method has higher prediction performance than existing alternatives.

Non-approximate Inference for Collective Graphical Models on Path Graphs via Discrete Difference of Convex Algorithm

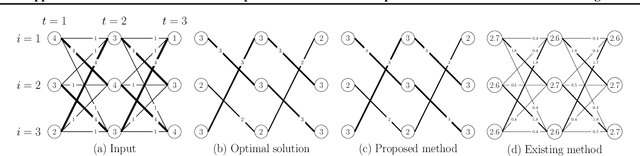
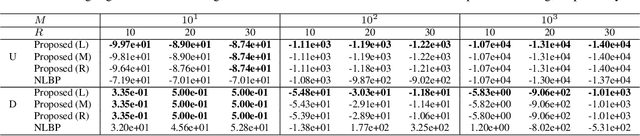
The importance of aggregated count data, which is calculated from the data of multiple individuals, continues to increase. Collective Graphical Model (CGM) is a probabilistic approach to the analysis of aggregated data. One of the most important operations in CGM is maximum a posteriori (MAP) inference of unobserved variables under given observations. Because the MAP inference problem for general CGMs has been shown to be NP-hard, an approach that solves an approximate problem has been proposed. However, this approach has two major drawbacks. First, the quality of the solution deteriorates when the values in the count tables are small, because the approximation becomes inaccurate. Second, since continuous relaxation is applied, the integrality constraints of the output are violated. To resolve these problems, this paper proposes a new method for MAP inference for CGMs on path graphs. First we show that the MAP inference problem can be formulated as a (non-linear) minimum cost flow problem. Then, we apply Difference of Convex Algorithm (DCA), which is a general methodology to minimize a function represented as the sum of a convex function and a concave function. In our algorithm, important subroutines in DCA can be efficiently calculated by minimum convex cost flow algorithms. Experiments show that the proposed method outputs higher quality solutions than the conventional approach.

Histogram Meets Topic Model: Density Estimation by Mixture of Histograms

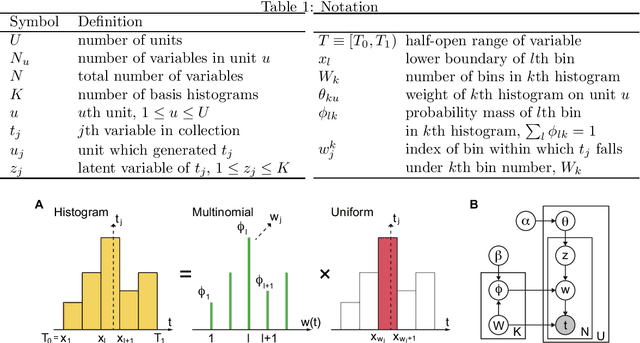
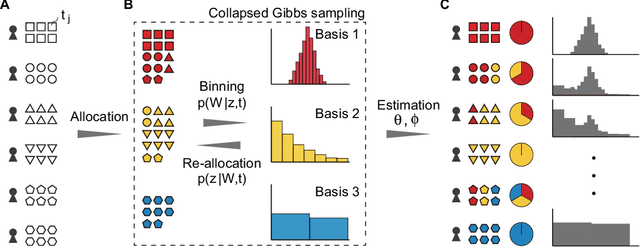
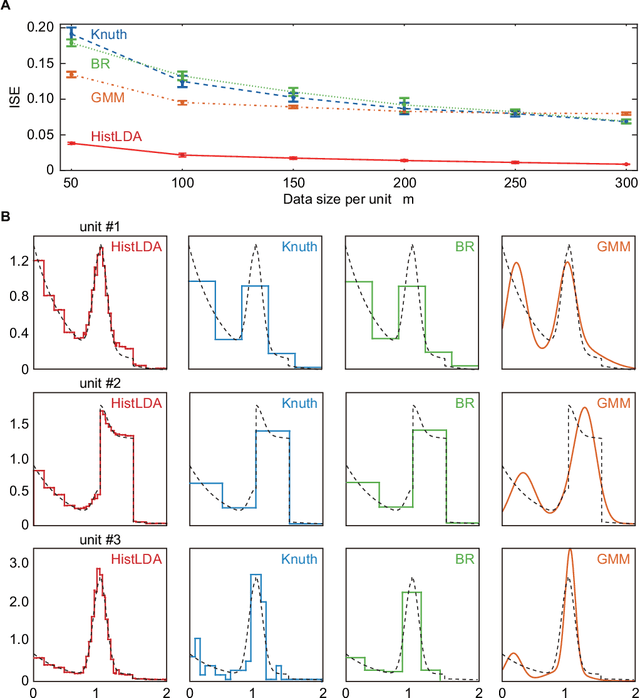
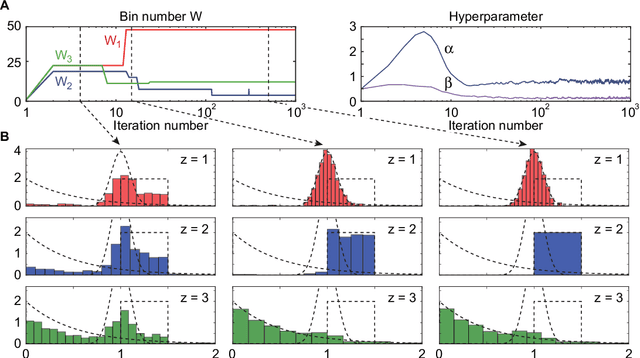
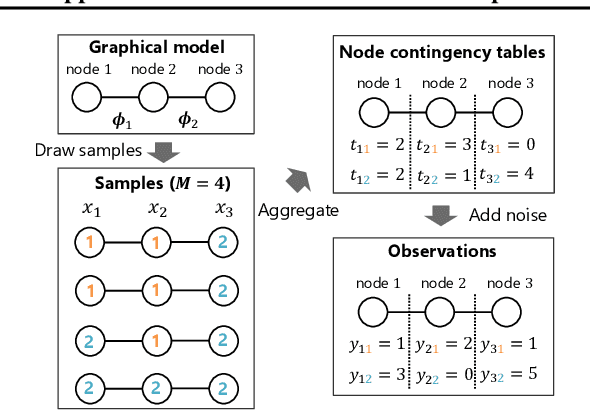
The histogram method is a powerful non-parametric approach for estimating the probability density function of a continuous variable. But the construction of a histogram, compared to the parametric approaches, demands a large number of observations to capture the underlying density function. Thus it is not suitable for analyzing a sparse data set, a collection of units with a small size of data. In this paper, by employing the probabilistic topic model, we develop a novel Bayesian approach to alleviating the sparsity problem in the conventional histogram estimation. Our method estimates a unit's density function as a mixture of basis histograms, in which the number of bins for each basis, as well as their heights, is determined automatically. The estimation procedure is performed by using the fast and easy-to-implement collapsed Gibbs sampling. We apply the proposed method to synthetic data, showing that it performs well.