Histogram Meets Topic Model: Density Estimation by Mixture of Histograms
Paper and Code
Dec 25, 2015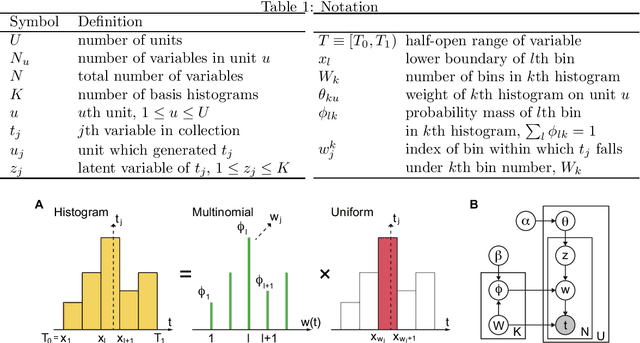
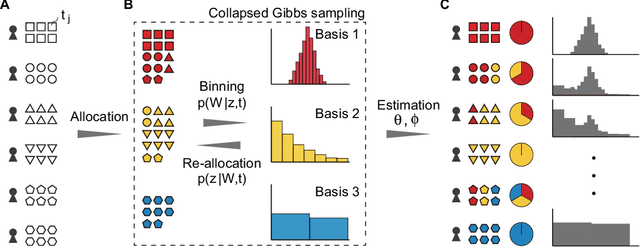
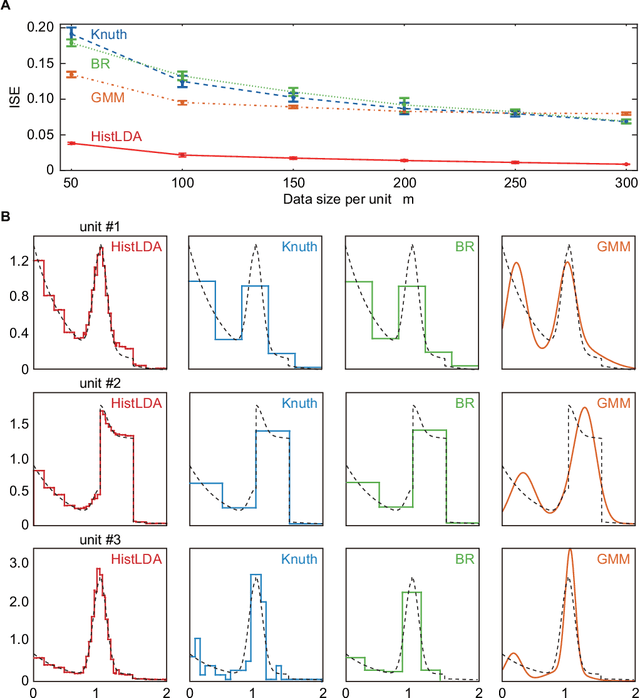
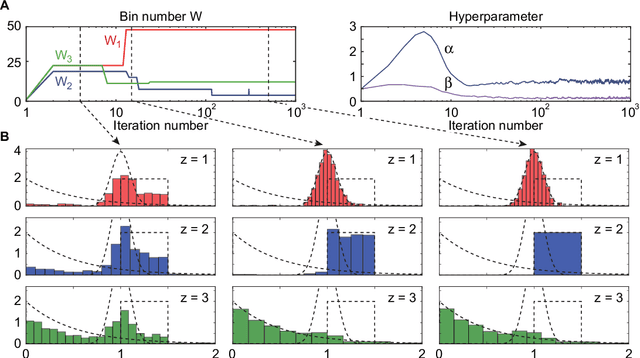
The histogram method is a powerful non-parametric approach for estimating the probability density function of a continuous variable. But the construction of a histogram, compared to the parametric approaches, demands a large number of observations to capture the underlying density function. Thus it is not suitable for analyzing a sparse data set, a collection of units with a small size of data. In this paper, by employing the probabilistic topic model, we develop a novel Bayesian approach to alleviating the sparsity problem in the conventional histogram estimation. Our method estimates a unit's density function as a mixture of basis histograms, in which the number of bins for each basis, as well as their heights, is determined automatically. The estimation procedure is performed by using the fast and easy-to-implement collapsed Gibbs sampling. We apply the proposed method to synthetic data, showing that it performs well.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge