Optimal Transport with Cyclic Symmetry

We propose novel fast algorithms for optimal transport (OT) utilizing a cyclic symmetry structure of input data. Such OT with cyclic symmetry appears universally in various real-world examples: image processing, urban planning, and graph processing. Our main idea is to reduce OT to a small optimization problem that has significantly fewer variables by utilizing cyclic symmetry and various optimization techniques. On the basis of this reduction, our algorithms solve the small optimization problem instead of the original OT. As a result, our algorithms obtain the optimal solution and the objective function value of the original OT faster than solving the original OT directly. In this paper, our focus is on two crucial OT formulations: the linear programming OT (LOT) and the strongly convex-regularized OT, which includes the well-known entropy-regularized OT (EROT). Experiments show the effectiveness of our algorithms for LOT and EROT in synthetic/real-world data that has a strict/approximate cyclic symmetry structure. Through theoretical and experimental results, this paper successfully introduces the concept of symmetry into the OT research field for the first time.

Aggregated Multi-output Gaussian Processes with Knowledge Transfer Across Domains

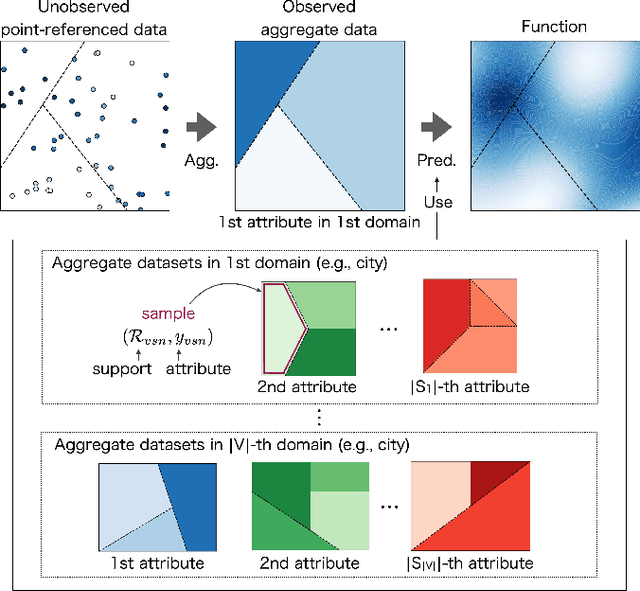
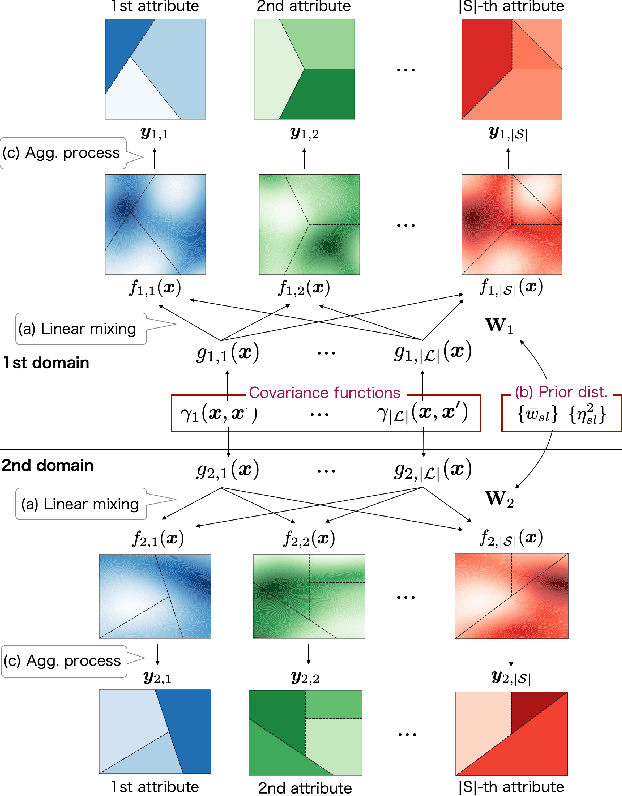
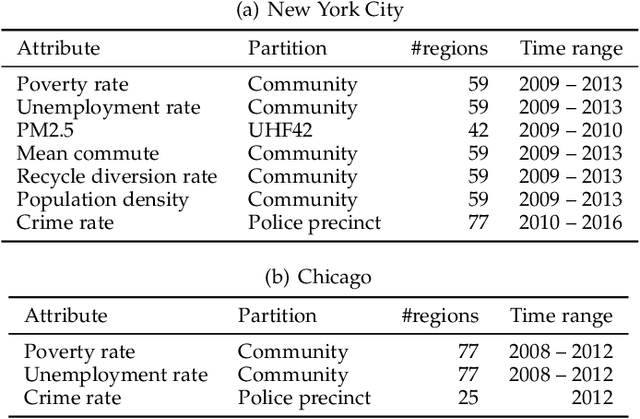
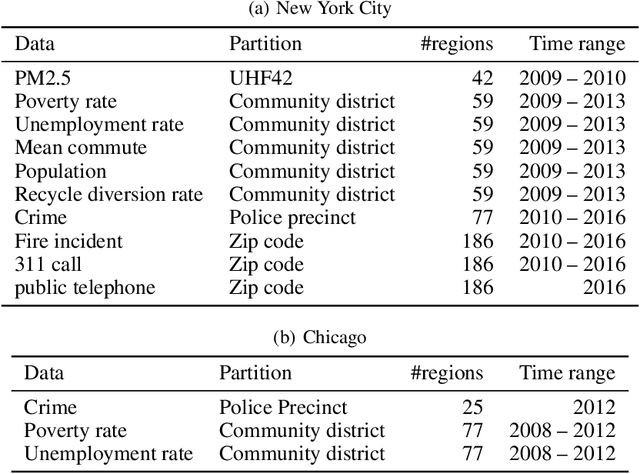
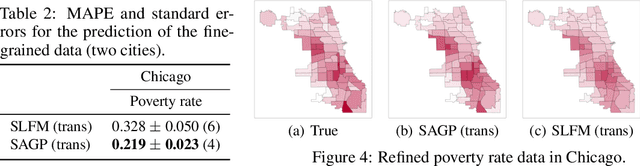
Aggregate data often appear in various fields such as socio-economics and public security. The aggregate data are associated not with points but with supports (e.g., spatial regions in a city). Since the supports may have various granularities depending on attributes (e.g., poverty rate and crime rate), modeling such data is not straightforward. This article offers a multi-output Gaussian process (MoGP) model that infers functions for attributes using multiple aggregate datasets of respective granularities. In the proposed model, the function for each attribute is assumed to be a dependent GP modeled as a linear mixing of independent latent GPs. We design an observation model with an aggregation process for each attribute; the process is an integral of the GP over the corresponding support. We also introduce a prior distribution of the mixing weights, which allows a knowledge transfer across domains (e.g., cities) by sharing the prior. This is advantageous in such a situation where the spatially aggregated dataset in a city is too coarse to interpolate; the proposed model can still make accurate predictions of attributes by utilizing aggregate datasets in other cities. The inference of the proposed model is based on variational Bayes, which enables one to learn the model parameters using the aggregate datasets from multiple domains. The experiments demonstrate that the proposed model outperforms in the task of refining coarse-grained aggregate data on real-world datasets: Time series of air pollutants in Beijing and various kinds of spatial datasets from New York City and Chicago.

Non-approximate Inference for Collective Graphical Models on Path Graphs via Discrete Difference of Convex Algorithm

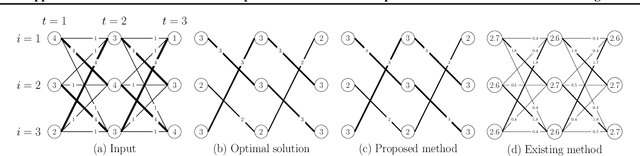
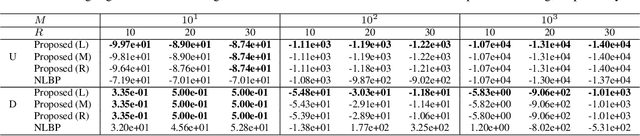
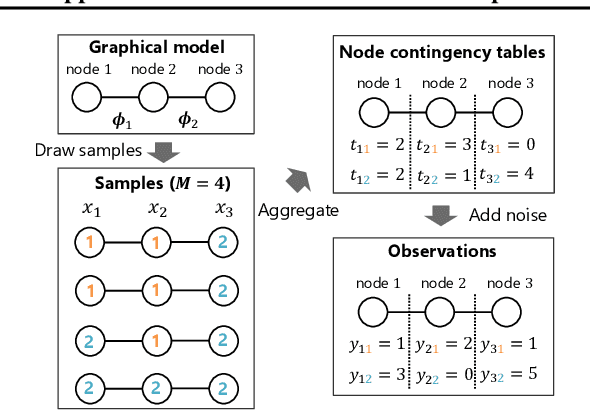
The importance of aggregated count data, which is calculated from the data of multiple individuals, continues to increase. Collective Graphical Model (CGM) is a probabilistic approach to the analysis of aggregated data. One of the most important operations in CGM is maximum a posteriori (MAP) inference of unobserved variables under given observations. Because the MAP inference problem for general CGMs has been shown to be NP-hard, an approach that solves an approximate problem has been proposed. However, this approach has two major drawbacks. First, the quality of the solution deteriorates when the values in the count tables are small, because the approximation becomes inaccurate. Second, since continuous relaxation is applied, the integrality constraints of the output are violated. To resolve these problems, this paper proposes a new method for MAP inference for CGMs on path graphs. First we show that the MAP inference problem can be formulated as a (non-linear) minimum cost flow problem. Then, we apply Difference of Convex Algorithm (DCA), which is a general methodology to minimize a function represented as the sum of a convex function and a concave function. In our algorithm, important subroutines in DCA can be efficiently calculated by minimum convex cost flow algorithms. Experiments show that the proposed method outputs higher quality solutions than the conventional approach.

Probabilistic Optimal Transport based on Collective Graphical Models

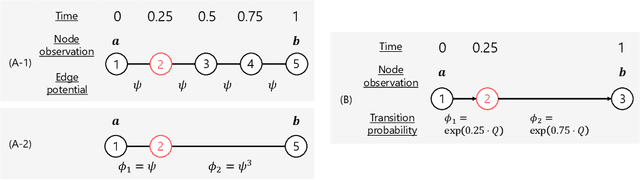
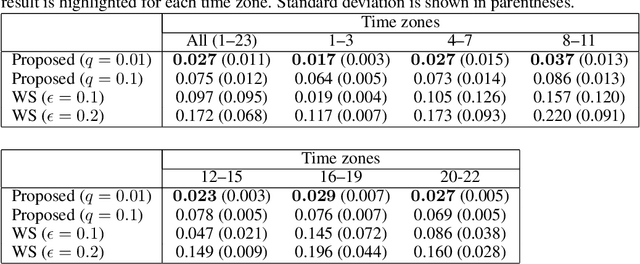
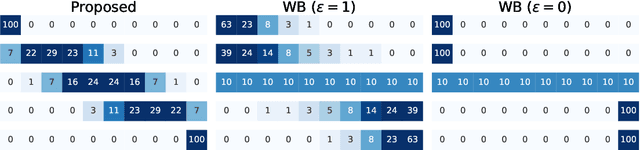
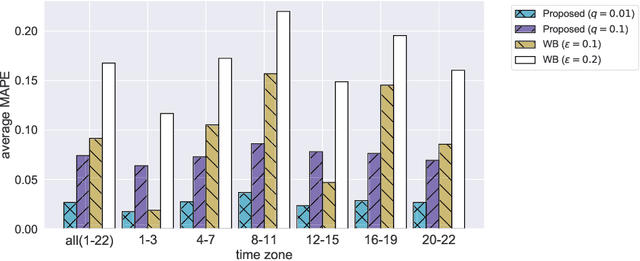
Optimal Transport (OT) is being widely used in various fields such as machine learning and computer vision, as it is a powerful tool for measuring the similarity between probability distributions and histograms. In previous studies, OT has been defined as the minimum cost to transport probability mass from one probability distribution to another. In this study, we propose a new framework in which OT is considered as a maximum a posteriori (MAP) solution of a probabilistic generative model. With the proposed framework, we show that OT with entropic regularization is equivalent to maximizing a posterior probability of a probabilistic model called Collective Graphical Model (CGM), which describes aggregated statistics of multiple samples generated from a graphical model. Interpreting OT as a MAP solution of a CGM has the following two advantages: (i) We can calculate the discrepancy between noisy histograms by modeling noise distributions. Since various distributions can be used for noise modeling, it is possible to select the noise distribution flexibly to suit the situation. (ii) We can construct a new method for interpolation between histograms, which is an important application of OT. The proposed method allows for intuitive modeling based on the probabilistic interpretations, and a simple and efficient estimation algorithm is available. Experiments using synthetic and real-world spatio-temporal population datasets show the effectiveness of the proposed interpolation method.

Spatially Aggregated Gaussian Processes with Multivariate Areal Outputs

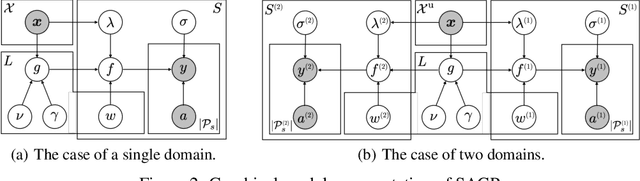
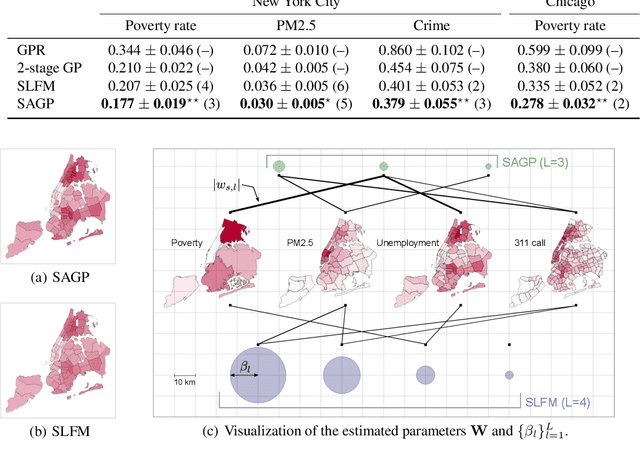
We propose a probabilistic model for inferring the multivariate function from multiple areal data sets with various granularities. Here, the areal data are observed not at location points but at regions. Existing regression-based models require the fine-grained auxiliary data sets on the same domain. With the proposed model, the functions for respective areal data sets are assumed to be a multivariate dependent Gaussian process (GP) that is modeled as a linear mixing of independent latent GPs. Sharing of latent GPs across multiple areal data sets allows us to effectively estimate spatial correlation for each areal data set; moreover it can easily be extended to transfer learning across multiple domains. To handle the multivariate areal data, we design its observation model with a spatial aggregation process for each areal data set, which is an integral of the mixed GP over the corresponding region. By deriving the posterior GP, we can predict the data value at any location point by considering the spatial correlations and the dependences between areal data sets simultaneously. Our experiments on real-world data sets demonstrate that our model can 1) accurately refine the coarse-grained areal data, and 2) offer performance improvements by using the areal data sets from multiple domains.