Aggregated Multi-output Gaussian Processes with Knowledge Transfer Across Domains
Paper and Code
Jun 24, 2022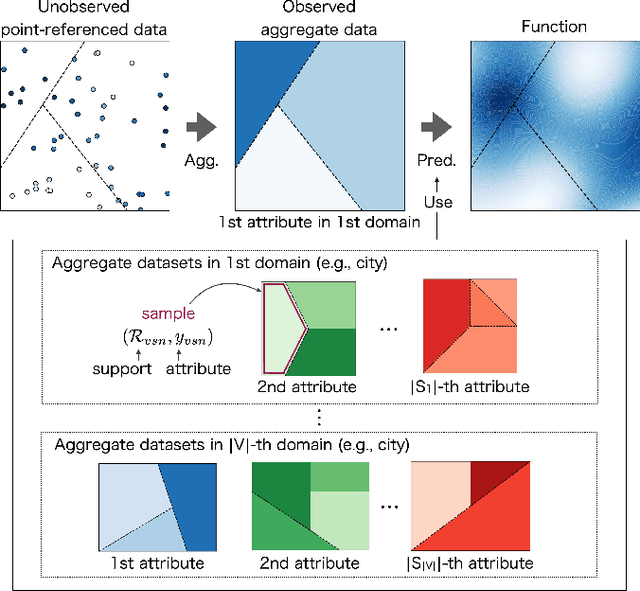

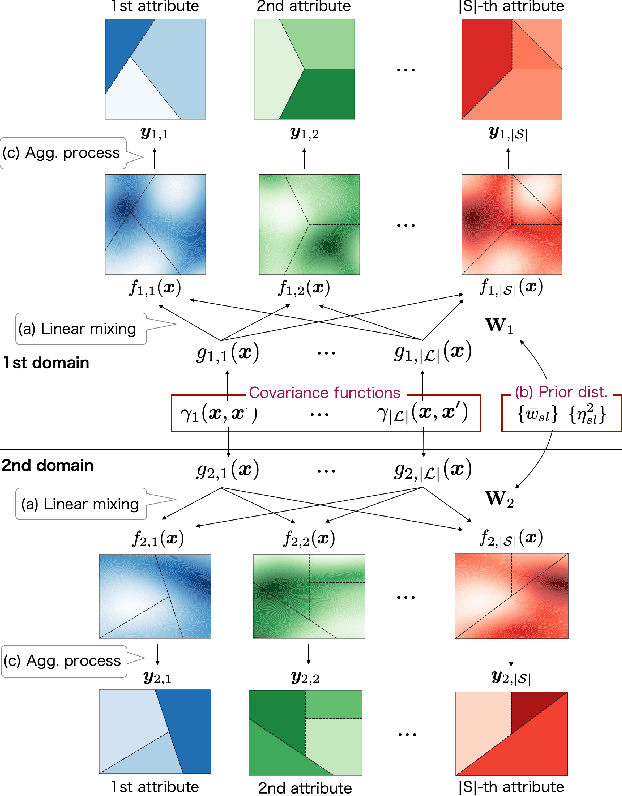
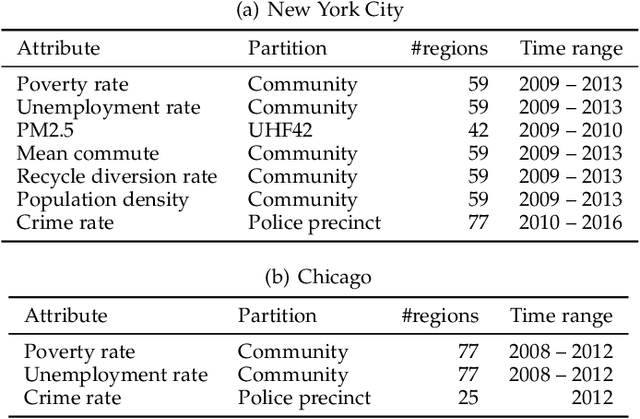
Aggregate data often appear in various fields such as socio-economics and public security. The aggregate data are associated not with points but with supports (e.g., spatial regions in a city). Since the supports may have various granularities depending on attributes (e.g., poverty rate and crime rate), modeling such data is not straightforward. This article offers a multi-output Gaussian process (MoGP) model that infers functions for attributes using multiple aggregate datasets of respective granularities. In the proposed model, the function for each attribute is assumed to be a dependent GP modeled as a linear mixing of independent latent GPs. We design an observation model with an aggregation process for each attribute; the process is an integral of the GP over the corresponding support. We also introduce a prior distribution of the mixing weights, which allows a knowledge transfer across domains (e.g., cities) by sharing the prior. This is advantageous in such a situation where the spatially aggregated dataset in a city is too coarse to interpolate; the proposed model can still make accurate predictions of attributes by utilizing aggregate datasets in other cities. The inference of the proposed model is based on variational Bayes, which enables one to learn the model parameters using the aggregate datasets from multiple domains. The experiments demonstrate that the proposed model outperforms in the task of refining coarse-grained aggregate data on real-world datasets: Time series of air pollutants in Beijing and various kinds of spatial datasets from New York City and Chicago.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge