ICLR: In-Context Learning of Representations

Recent work has demonstrated that semantics specified by pretraining data influence how representations of different concepts are organized in a large language model (LLM). However, given the open-ended nature of LLMs, e.g., their ability to in-context learn, we can ask whether models alter these pretraining semantics to adopt alternative, context-specified ones. Specifically, if we provide in-context exemplars wherein a concept plays a different role than what the pretraining data suggests, do models reorganize their representations in accordance with these novel semantics? To answer this question, we take inspiration from the theory of conceptual role semantics and define a toy "graph tracing" task wherein the nodes of the graph are referenced via concepts seen during training (e.g., apple, bird, etc.) and the connectivity of the graph is defined via some predefined structure (e.g., a square grid). Given exemplars that indicate traces of random walks on the graph, we analyze intermediate representations of the model and find that as the amount of context is scaled, there is a sudden re-organization from pretrained semantic representations to in-context representations aligned with the graph structure. Further, we find that when reference concepts have correlations in their semantics (e.g., Monday, Tuesday, etc.), the context-specified graph structure is still present in the representations, but is unable to dominate the pretrained structure. To explain these results, we analogize our task to energy minimization for a predefined graph topology, providing evidence towards an implicit optimization process to infer context-specified semantics. Overall, our findings indicate scaling context-size can flexibly re-organize model representations, possibly unlocking novel capabilities.

Representation Shattering in Transformers: A Synthetic Study with Knowledge Editing

Knowledge Editing (KE) algorithms alter models' internal weights to perform targeted updates to incorrect, outdated, or otherwise unwanted factual associations. In order to better define the possibilities and limitations of these approaches, recent work has shown that applying KE can adversely affect models' factual recall accuracy and diminish their general reasoning abilities. While these studies give broad insights into the potential harms of KE algorithms, e.g., via performance evaluations on benchmarks, we argue little is understood as to why such destructive failures occur. Is it possible KE methods distort representations of concepts beyond the targeted fact, hence hampering abilities at broad? If so, what is the extent of this distortion? To take a step towards addressing such questions, we define a novel synthetic task wherein a Transformer is trained from scratch to internalize a ``structured'' knowledge graph. The structure enforces relationships between entities of the graph, such that editing a factual association has "trickling effects" on other entities in the graph (e.g., altering X's parent is Y to Z affects who X's siblings' parent is). Through evaluations of edited models and analysis of extracted representations, we show that KE inadvertently affects representations of entities beyond the targeted one, distorting relevant structures that allow a model to infer unseen knowledge about an entity. We call this phenomenon representation shattering and demonstrate that it results in degradation of factual recall and reasoning performance more broadly. To corroborate our findings in a more naturalistic setup, we perform preliminary experiments with a pretrained GPT-2-XL model and reproduce the representation shattering effect therein as well. Overall, our work yields a precise mechanistic hypothesis to explain why KE has adverse effects on model capabilities.

Dynamics of Concept Learning and Compositional Generalization

Prior work has shown that text-conditioned diffusion models can learn to identify and manipulate primitive concepts underlying a compositional data-generating process, enabling generalization to entirely novel, out-of-distribution compositions. Beyond performance evaluations, these studies develop a rich empirical phenomenology of learning dynamics, showing that models generalize sequentially, respecting the compositional hierarchy of the data-generating process. Moreover, concept-centric structures within the data significantly influence a model's speed of learning the ability to manipulate a concept. In this paper, we aim to better characterize these empirical results from a theoretical standpoint. Specifically, we propose an abstraction of prior work's compositional generalization problem by introducing a structured identity mapping (SIM) task, where a model is trained to learn the identity mapping on a Gaussian mixture with structurally organized centroids. We mathematically analyze the learning dynamics of neural networks trained on this SIM task and show that, despite its simplicity, SIM's learning dynamics capture and help explain key empirical observations on compositional generalization with diffusion models identified in prior work. Our theory also offers several new insights -- e.g., we find a novel mechanism for non-monotonic learning dynamics of test loss in early phases of training. We validate our new predictions by training a text-conditioned diffusion model, bridging our simplified framework and complex generative models. Overall, this work establishes the SIM task as a meaningful theoretical abstraction of concept learning dynamics in modern generative models.

Emergence of Hidden Capabilities: Exploring Learning Dynamics in Concept Space

Modern generative models demonstrate impressive capabilities, likely stemming from an ability to identify and manipulate abstract concepts underlying their training data. However, fundamental questions remain: what determines the concepts a model learns, the order in which it learns them, and its ability to manipulate those concepts? To address these questions, we propose analyzing a model's learning dynamics via a framework we call the concept space, where each axis represents an independent concept underlying the data generating process. By characterizing learning dynamics in this space, we identify how the speed at which a concept is learned, and hence the order of concept learning, is controlled by properties of the data we term concept signal. Further, we observe moments of sudden turns in the direction of a model's learning dynamics in concept space. Surprisingly, these points precisely correspond to the emergence of hidden capabilities, i.e., where latent interventions show the model possesses the capability to manipulate a concept, but these capabilities cannot yet be elicited via naive input prompting. While our results focus on synthetically defined toy datasets, we hypothesize a general claim on emergence of hidden capabilities may hold: generative models possess latent capabilities that emerge suddenly and consistently during training, though a model might not exhibit these capabilities under naive input prompting.

Towards an Understanding of Stepwise Inference in Transformers: A Synthetic Graph Navigation Model

Stepwise inference protocols, such as scratchpads and chain-of-thought, help language models solve complex problems by decomposing them into a sequence of simpler subproblems. Despite the significant gain in performance achieved via these protocols, the underlying mechanisms of stepwise inference have remained elusive. To address this, we propose to study autoregressive Transformer models on a synthetic task that embodies the multi-step nature of problems where stepwise inference is generally most useful. Specifically, we define a graph navigation problem wherein a model is tasked with traversing a path from a start to a goal node on the graph. Despite is simplicity, we find we can empirically reproduce and analyze several phenomena observed at scale: (i) the stepwise inference reasoning gap, the cause of which we find in the structure of the training data; (ii) a diversity-accuracy tradeoff in model generations as sampling temperature varies; (iii) a simplicity bias in the model's output; and (iv) compositional generalization and a primacy bias with in-context exemplars. Overall, our work introduces a grounded, synthetic framework for studying stepwise inference and offers mechanistic hypotheses that can lay the foundation for a deeper understanding of this phenomenon.

Meta-Learning for Neural Network-based Temporal Point Processes

Human activities generate various event sequences such as taxi trip records, bike-sharing pick-ups, crime occurrence, and infectious disease transmission. The point process is widely used in many applications to predict such events related to human activities. However, point processes present two problems in predicting events related to human activities. First, recent high-performance point process models require the input of sufficient numbers of events collected over a long period (i.e., long sequences) for training, which are often unavailable in realistic situations. Second, the long-term predictions required in real-world applications are difficult. To tackle these problems, we propose a novel meta-learning approach for periodicity-aware prediction of future events given short sequences. The proposed method first embeds short sequences into hidden representations (i.e., task representations) via recurrent neural networks for creating predictions from short sequences. It then models the intensity of the point process by monotonic neural networks (MNNs), with the input being the task representations. We transfer the prior knowledge learned from related tasks and can improve event prediction given short sequences of target tasks. We design the MNNs to explicitly take temporal periodic patterns into account, contributing to improved long-term prediction performance. Experiments on multiple real-world datasets demonstrate that the proposed method has higher prediction performance than existing alternatives.

Compositional Abilities Emerge Multiplicatively: Exploring Diffusion Models on a Synthetic Task

Modern generative models exhibit unprecedented capabilities to generate extremely realistic data. However, given the inherent compositionality of the real world, reliable use of these models in practical applications requires that they exhibit the capability to compose a novel set of concepts to generate outputs not seen in the training data set. Prior work demonstrates that recent diffusion models do exhibit intriguing compositional generalization abilities, but also fail unpredictably. Motivated by this, we perform a controlled study for understanding compositional generalization in conditional diffusion models in a synthetic setting, varying different attributes of the training data and measuring the model's ability to generate samples out-of-distribution. Our results show: (i) the order in which the ability to generate samples from a concept and compose them emerges is governed by the structure of the underlying data-generating process; (ii) performance on compositional tasks exhibits a sudden ``emergence'' due to multiplicative reliance on the performance of constituent tasks, partially explaining emergent phenomena seen in generative models; and (iii) composing concepts with lower frequency in the training data to generate out-of-distribution samples requires considerably more optimization steps compared to generating in-distribution samples. Overall, our study lays a foundation for understanding capabilities and compositionality in generative models from a data-centric perspective.

Predicting Opinion Dynamics via Sociologically-Informed Neural Networks

Opinion formation and propagation are crucial phenomena in social networks and have been extensively studied across several disciplines. Traditionally, theoretical models of opinion dynamics have been proposed to describe the interactions between individuals (i.e., social interaction) and their impact on the evolution of collective opinions. Although these models can incorporate sociological and psychological knowledge on the mechanisms of social interaction, they demand extensive calibration with real data to make reliable predictions, requiring much time and effort. Recently, the widespread use of social media platforms provides new paradigms to learn deep learning models from a large volume of social media data. However, these methods ignore any scientific knowledge about the mechanism of social interaction. In this work, we present the first hybrid method called Sociologically-Informed Neural Network (SINN), which integrates theoretical models and social media data by transporting the concepts of physics-informed neural networks (PINNs) from natural science (i.e., physics) into social science (i.e., sociology and social psychology). In particular, we recast theoretical models as ordinary differential equations (ODEs). Then we train a neural network that simultaneously approximates the data and conforms to the ODEs that represent the social scientific knowledge. In addition, we extend PINNs by integrating matrix factorization and a language model to incorporate rich side information (e.g., user profiles) and structural knowledge (e.g., cluster structure of the social interaction network). Moreover, we develop an end-to-end training procedure for SINN, which involves Gumbel-Softmax approximation to include stochastic mechanisms of social interaction. Extensive experiments on real-world and synthetic datasets show SINN outperforms six baseline methods in predicting opinion dynamics.

Aggregated Multi-output Gaussian Processes with Knowledge Transfer Across Domains

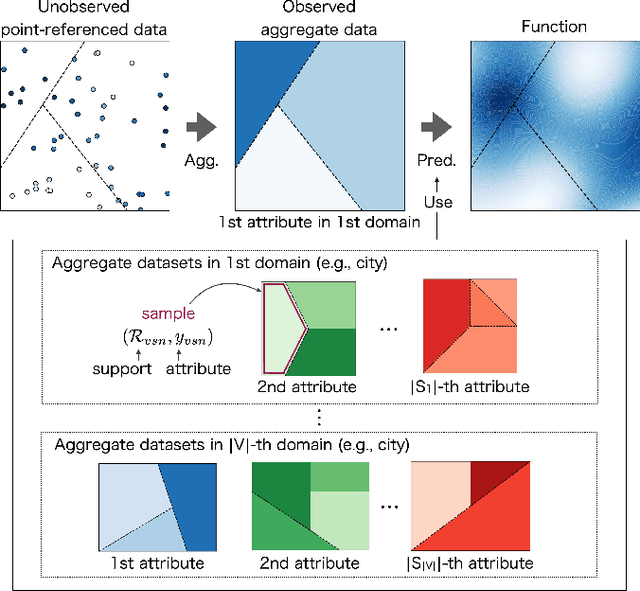
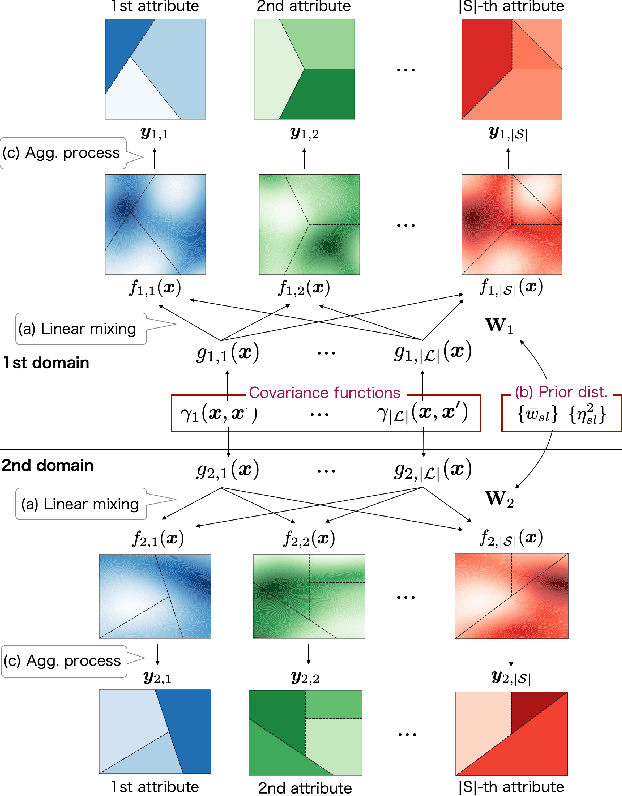
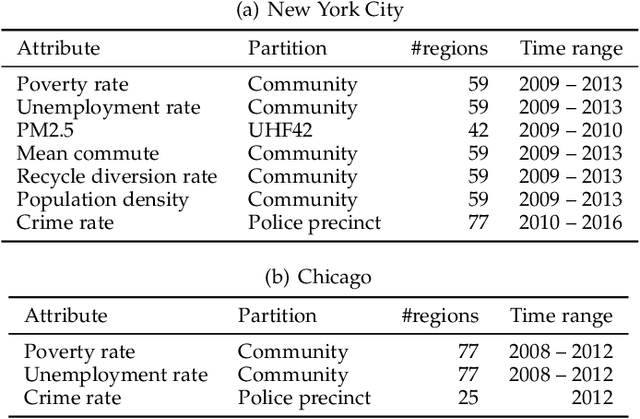
Aggregate data often appear in various fields such as socio-economics and public security. The aggregate data are associated not with points but with supports (e.g., spatial regions in a city). Since the supports may have various granularities depending on attributes (e.g., poverty rate and crime rate), modeling such data is not straightforward. This article offers a multi-output Gaussian process (MoGP) model that infers functions for attributes using multiple aggregate datasets of respective granularities. In the proposed model, the function for each attribute is assumed to be a dependent GP modeled as a linear mixing of independent latent GPs. We design an observation model with an aggregation process for each attribute; the process is an integral of the GP over the corresponding support. We also introduce a prior distribution of the mixing weights, which allows a knowledge transfer across domains (e.g., cities) by sharing the prior. This is advantageous in such a situation where the spatially aggregated dataset in a city is too coarse to interpolate; the proposed model can still make accurate predictions of attributes by utilizing aggregate datasets in other cities. The inference of the proposed model is based on variational Bayes, which enables one to learn the model parameters using the aggregate datasets from multiple domains. The experiments demonstrate that the proposed model outperforms in the task of refining coarse-grained aggregate data on real-world datasets: Time series of air pollutants in Beijing and various kinds of spatial datasets from New York City and Chicago.

Dynamic Hawkes Processes for Discovering Time-evolving Communities' States behind Diffusion Processes

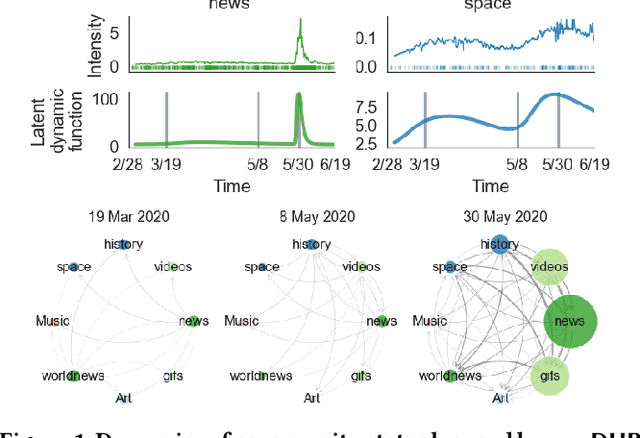
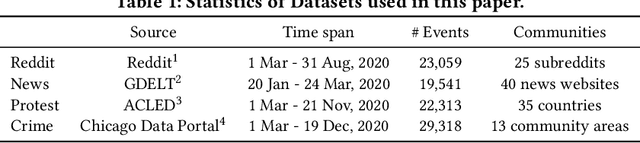
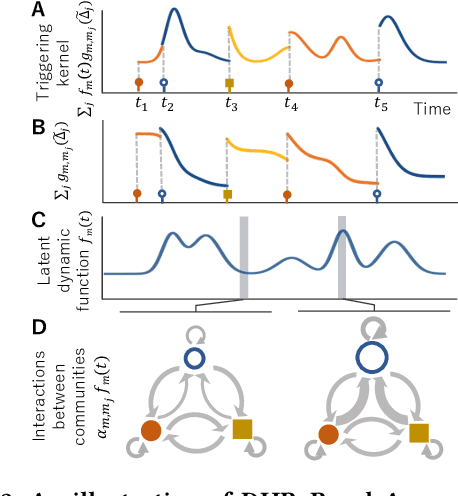
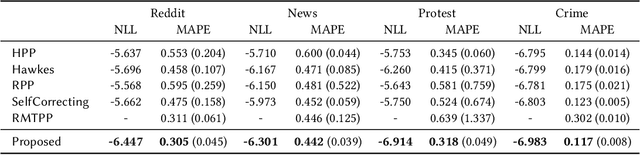
Sequences of events including infectious disease outbreaks, social network activities, and crimes are ubiquitous and the data on such events carry essential information about the underlying diffusion processes between communities (e.g., regions, online user groups). Modeling diffusion processes and predicting future events are crucial in many applications including epidemic control, viral marketing, and predictive policing. Hawkes processes offer a central tool for modeling the diffusion processes, in which the influence from the past events is described by the triggering kernel. However, the triggering kernel parameters, which govern how each community is influenced by the past events, are assumed to be static over time. In the real world, the diffusion processes depend not only on the influences from the past, but also the current (time-evolving) states of the communities, e.g., people's awareness of the disease and people's current interests. In this paper, we propose a novel Hawkes process model that is able to capture the underlying dynamics of community states behind the diffusion processes and predict the occurrences of events based on the dynamics. Specifically, we model the latent dynamic function that encodes these hidden dynamics by a mixture of neural networks. Then we design the triggering kernel using the latent dynamic function and its integral. The proposed method, termed DHP (Dynamic Hawkes Processes), offers a flexible way to learn complex representations of the time-evolving communities' states, while at the same time it allows to computing the exact likelihood, which makes parameter learning tractable. Extensive experiments on four real-world event datasets show that DHP outperforms five widely adopted methods for event prediction.