Prospective Learning: Learning for a Dynamic Future

In real-world applications, the distribution of the data, and our goals, evolve over time. The prevailing theoretical framework for studying machine learning, namely probably approximately correct (PAC) learning, largely ignores time. As a consequence, existing strategies to address the dynamic nature of data and goals exhibit poor real-world performance. This paper develops a theoretical framework called "Prospective Learning" that is tailored for situations when the optimal hypothesis changes over time. In PAC learning, empirical risk minimization (ERM) is known to be consistent. We develop a learner called Prospective ERM, which returns a sequence of predictors that make predictions on future data. We prove that the risk of prospective ERM converges to the Bayes risk under certain assumptions on the stochastic process generating the data. Prospective ERM, roughly speaking, incorporates time as an input in addition to the data. We show that standard ERM as done in PAC learning, without incorporating time, can result in failure to learn when distributions are dynamic. Numerical experiments illustrate that prospective ERM can learn synthetic and visual recognition problems constructed from MNIST and CIFAR-10.

Representation Shattering in Transformers: A Synthetic Study with Knowledge Editing

Knowledge Editing (KE) algorithms alter models' internal weights to perform targeted updates to incorrect, outdated, or otherwise unwanted factual associations. In order to better define the possibilities and limitations of these approaches, recent work has shown that applying KE can adversely affect models' factual recall accuracy and diminish their general reasoning abilities. While these studies give broad insights into the potential harms of KE algorithms, e.g., via performance evaluations on benchmarks, we argue little is understood as to why such destructive failures occur. Is it possible KE methods distort representations of concepts beyond the targeted fact, hence hampering abilities at broad? If so, what is the extent of this distortion? To take a step towards addressing such questions, we define a novel synthetic task wherein a Transformer is trained from scratch to internalize a ``structured'' knowledge graph. The structure enforces relationships between entities of the graph, such that editing a factual association has "trickling effects" on other entities in the graph (e.g., altering X's parent is Y to Z affects who X's siblings' parent is). Through evaluations of edited models and analysis of extracted representations, we show that KE inadvertently affects representations of entities beyond the targeted one, distorting relevant structures that allow a model to infer unseen knowledge about an entity. We call this phenomenon representation shattering and demonstrate that it results in degradation of factual recall and reasoning performance more broadly. To corroborate our findings in a more naturalistic setup, we perform preliminary experiments with a pretrained GPT-2-XL model and reproduce the representation shattering effect therein as well. Overall, our work yields a precise mechanistic hypothesis to explain why KE has adverse effects on model capabilities.

Many Perception Tasks are Highly Redundant Functions of their Input Data

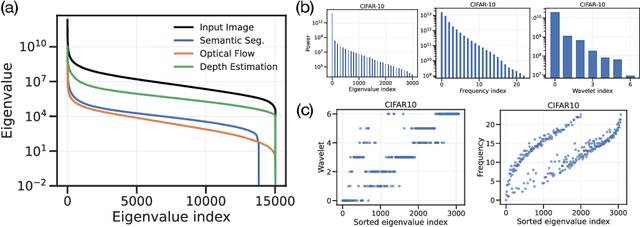
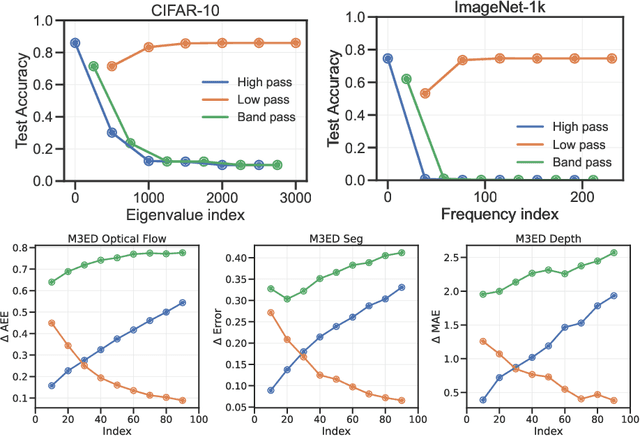
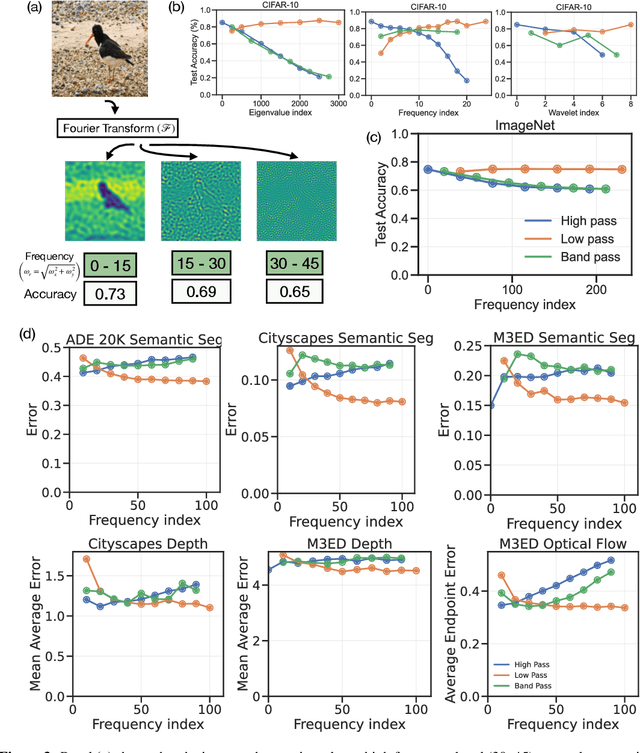
We show that many perception tasks, from visual recognition, semantic segmentation, optical flow, depth estimation to vocalization discrimination, are highly redundant functions of their input data. Images or spectrograms, projected into different subspaces, formed by orthogonal bases in pixel, Fourier or wavelet domains, can be used to solve these tasks remarkably well regardless of whether it is the top subspace where data varies the most, some intermediate subspace with moderate variability--or the bottom subspace where data varies the least. This phenomenon occurs because different subspaces have a large degree of redundant information relevant to the task.

Towards an Understanding of Stepwise Inference in Transformers: A Synthetic Graph Navigation Model

Stepwise inference protocols, such as scratchpads and chain-of-thought, help language models solve complex problems by decomposing them into a sequence of simpler subproblems. Despite the significant gain in performance achieved via these protocols, the underlying mechanisms of stepwise inference have remained elusive. To address this, we propose to study autoregressive Transformer models on a synthetic task that embodies the multi-step nature of problems where stepwise inference is generally most useful. Specifically, we define a graph navigation problem wherein a model is tasked with traversing a path from a start to a goal node on the graph. Despite is simplicity, we find we can empirically reproduce and analyze several phenomena observed at scale: (i) the stepwise inference reasoning gap, the cause of which we find in the structure of the training data; (ii) a diversity-accuracy tradeoff in model generations as sampling temperature varies; (iii) a simplicity bias in the model's output; and (iv) compositional generalization and a primacy bias with in-context exemplars. Overall, our work introduces a grounded, synthetic framework for studying stepwise inference and offers mechanistic hypotheses that can lay the foundation for a deeper understanding of this phenomenon.

How Capable Can a Transformer Become? A Study on Synthetic, Interpretable Tasks

Transformers trained on huge text corpora exhibit a remarkable set of capabilities, e.g., performing simple logical operations. Given the inherent compositional nature of language, one can expect the model to learn to compose these capabilities, potentially yielding a combinatorial explosion of what operations it can perform on an input. Motivated by the above, we aim to assess in this paper "how capable can a transformer become?". Specifically, we train autoregressive Transformer models on a data-generating process that involves compositions of a set of well-defined monolithic capabilities. Through a series of extensive and systematic experiments on this data-generating process, we show that: (1) autoregressive Transformers can learn compositional structures from the training data and generalize to exponentially or even combinatorially many functions; (2) composing functions by generating intermediate outputs is more effective at generalizing to unseen compositions, compared to generating no intermediate outputs; (3) the training data has a significant impact on the model's ability to compose unseen combinations of functions; and (4) the attention layers in the latter half of the model are critical to compositionality.

The Training Process of Many Deep Networks Explores the Same Low-Dimensional Manifold

We develop information-geometric techniques to analyze the trajectories of the predictions of deep networks during training. By examining the underlying high-dimensional probabilistic models, we reveal that the training process explores an effectively low-dimensional manifold. Networks with a wide range of architectures, sizes, trained using different optimization methods, regularization techniques, data augmentation techniques, and weight initializations lie on the same manifold in the prediction space. We study the details of this manifold to find that networks with different architectures follow distinguishable trajectories but other factors have a minimal influence; larger networks train along a similar manifold as that of smaller networks, just faster; and networks initialized at very different parts of the prediction space converge to the solution along a similar manifold.

A picture of the space of typical learnable tasks

We develop a technique to analyze representations learned by deep networks when they are trained on different tasks using supervised, meta- and contrastive learning. We develop a technique to visualize such representations using an isometric embedding of the space of probabilistic models into a lower-dimensional space, i.e., one that preserves pairwise distances. We discover the following surprising phenomena that shed light upon the structure in the space of learnable tasks: (1) the manifold of probabilistic models trained on different tasks using different representation learning methods is effectively low-dimensional; (2) supervised learning on one task results in a surprising amount of progress on seemingly dissimilar tasks; progress on other tasks is larger if the training task has diverse classes; (3) the structure of the space of tasks indicated by our analysis is consistent with parts of the Wordnet phylogenetic tree; (4) fine-tuning a model upon a sub-task does not change the representation much if the model was trained for a large number of epochs; (5) episodic meta-learning algorithms fit similar models eventually as that of supervised learning, even if the two traverse different trajectories during training; (6) contrastive learning methods trained on different datasets learn similar representations. We use classification tasks constructed from the CIFAR-10 and Imagenet datasets to study these phenomena.

The Value of Out-of-Distribution Data

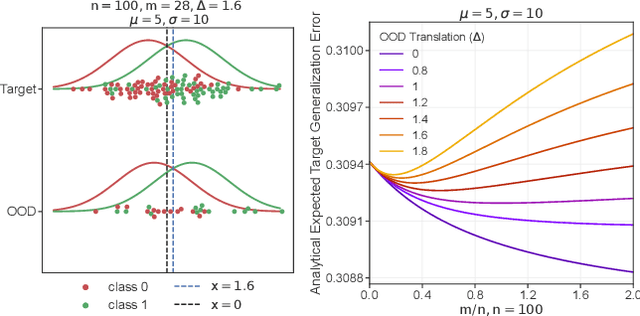
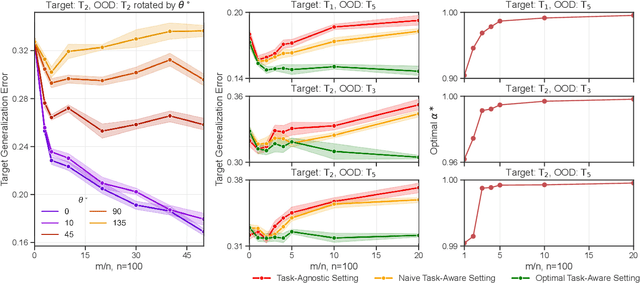
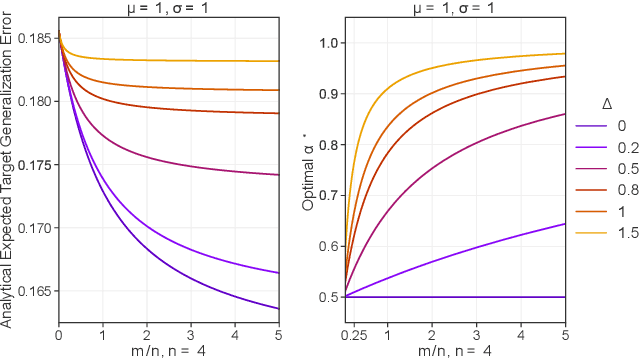
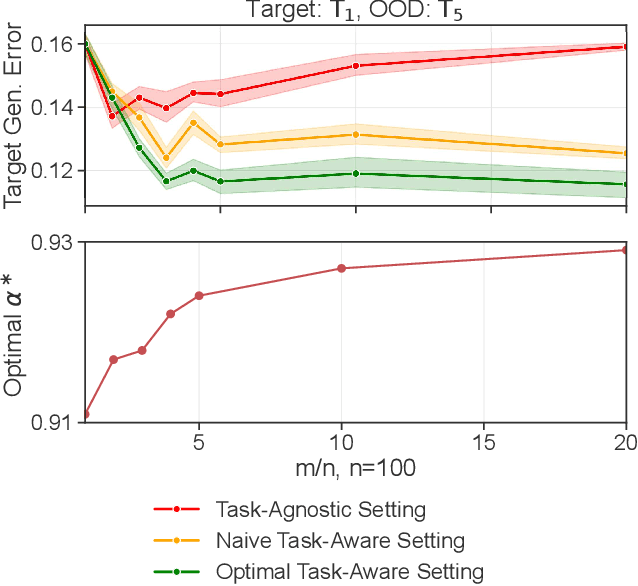
More data helps us generalize to a task. But real datasets can contain out-of-distribution (OOD) data; this can come in the form of heterogeneity such as intra-class variability but also in the form of temporal shifts or concept drifts. We demonstrate a counter-intuitive phenomenon for such problems: generalization error of the task can be a non-monotonic function of the number of OOD samples; a small number of OOD samples can improve generalization but if the number of OOD samples is beyond a threshold, then the generalization error can deteriorate. We also show that if we know which samples are OOD, then using a weighted objective between the target and OOD samples ensures that the generalization error decreases monotonically. We demonstrate and analyze this issue using linear classifiers on synthetic datasets and medium-sized neural networks on CIFAR-10.

Deep Reference Priors: What is the best way to pretrain a model?

What is the best way to exploit extra data -- be it unlabeled data from the same task, or labeled data from a related task -- to learn a given task? This paper formalizes the question using the theory of reference priors. Reference priors are objective, uninformative Bayesian priors that maximize the mutual information between the task and the weights of the model. Such priors enable the task to maximally affect the Bayesian posterior, e.g., reference priors depend upon the number of samples available for learning the task and for very small sample sizes, the prior puts more probability mass on low-complexity models in the hypothesis space. This paper presents the first demonstration of reference priors for medium-scale deep networks and image-based data. We develop generalizations of reference priors and demonstrate applications to two problems. First, by using unlabeled data to compute the reference prior, we develop new Bayesian semi-supervised learning methods that remain effective even with very few samples per class. Second, by using labeled data from the source task to compute the reference prior, we develop a new pretraining method for transfer learning that allows data from the target task to maximally affect the Bayesian posterior. Empirical validation of these methods is conducted on image classification datasets.

Boosting a Model Zoo for Multi-Task and Continual Learning

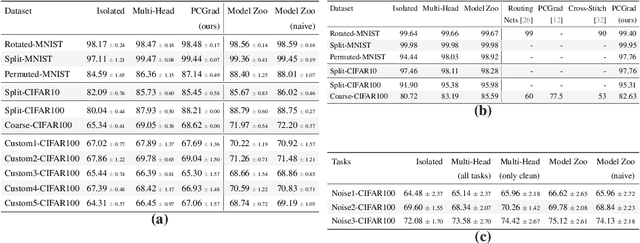
Leveraging data from multiple tasks, either all at once, or incrementally, to learn one model is an idea that lies at the heart of multi-task and continual learning methods. Ideally, such a model predicts each task more accurately than if the task were trained in isolation. We show using tools in statistical learning theory (i) how tasks can compete for capacity, i.e., including a particular task can deteriorate the accuracy on a given task, and (ii) that the ideal set of tasks that one should train together in order to perform well on a given task is different for different tasks. We develop methods to discover such competition in typical benchmark datasets which suggests that the prevalent practice of training with all tasks leaves performance on the table. This motivates our "Model Zoo", which is a boosting-based algorithm that builds an ensemble of models, each of which is very small, and it is trained on a smaller set of tasks. Model Zoo achieves large gains in prediction accuracy compared to state-of-the-art methods across a variety of existing benchmarks in multi-task and continual learning, as well as more challenging ones of our creation. We also show that even a model trained independently on all tasks outperforms all existing multi-task and continual learning methods.