SIGMA: Scalable Spectral Insights for LLM Collapse

The rapid adoption of synthetic data for training Large Language Models (LLMs) has introduced the technical challenge of "model collapse"-a degenerative process where recursive training on model-generated content leads to a contraction of distributional variance and representational quality. While the phenomenology of collapse is increasingly evident, rigorous methods to quantify and predict its onset in high-dimensional spaces remain elusive. In this paper, we introduce SIGMA (Spectral Inequalities for Gram Matrix Analysis), a unified framework that benchmarks model collapse through the spectral lens of the embedding Gram matrix. By deriving and utilizing deterministic and stochastic bounds on the matrix's spectrum, SIGMA provides a mathematically grounded metric to track the contraction of the representation space. Crucially, our stochastic formulation enables scalable estimation of these bounds, making the framework applicable to large-scale foundation models where full eigendecomposition is intractable. We demonstrate that SIGMA effectively captures the transition towards degenerate states, offering both theoretical insights into the mechanics of collapse and a practical, scalable tool for monitoring the health of recursive training pipelines.

Concentration bounds on response-based vector embeddings of black-box generative models

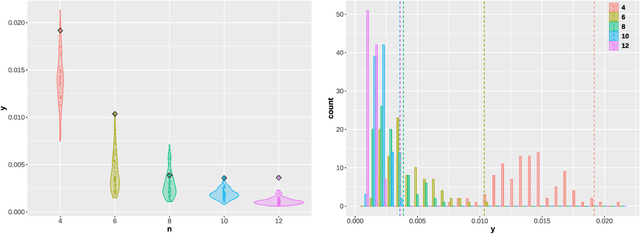
Generative models, such as large language models or text-to-image diffusion models, can generate relevant responses to user-given queries. Response-based vector embeddings of generative models facilitate statistical analysis and inference on a given collection of black-box generative models. The Data Kernel Perspective Space embedding is one particular method of obtaining response-based vector embeddings for a given set of generative models, already discussed in the literature. In this paper, under appropriate regularity conditions, we establish high probability concentration bounds on the sample vector embeddings for a given set of generative models, obtained through the method of Data Kernel Perspective Space embedding. Our results tell us the required number of sample responses needed in order to approximate the population-level vector embeddings with a desired level of accuracy. The algebraic tools used to establish our results can be used further for establishing concentration bounds on Classical Multidimensional Scaling embeddings in general, when the dissimilarities are observed with noise.

Graph Neural Networks Powered by Encoder Embedding for Improved Node Learning

Graph neural networks (GNNs) have emerged as a powerful framework for a wide range of node-level graph learning tasks. However, their performance is often constrained by reliance on random or minimally informed initial feature representations, which can lead to slow convergence and suboptimal solutions. In this paper, we leverage a statistically grounded method, one-hot graph encoder embedding (GEE), to generate high-quality initial node features that enhance the end-to-end training of GNNs. We refer to this integrated framework as the GEE-powered GNN (GG), and demonstrate its effectiveness through extensive simulations and real-world experiments across both unsupervised and supervised settings. In node clustering, GG consistently achieves state-of-the-art performance, ranking first across all evaluated real-world datasets, while exhibiting faster convergence compared to the standard GNN. For node classification, we further propose an enhanced variant, GG-C, which concatenates the outputs of GG and GEE and outperforms competing baselines. These results confirm the importance of principled, structure-aware feature initialization in realizing the full potential of GNNs.

Out-of-Sample Embedding with Proximity Data: Projection versus Restricted Reconstruction

The problem of using proximity (similarity or dissimilarity) data for the purpose of "adding a point to a vector diagram" was first studied by J.C. Gower in 1968. Since then, a number of methods -- mostly kernel methods -- have been proposed for solving what has come to be called the problem of *out-of-sample embedding*. We survey the various kernel methods that we have encountered and show that each can be derived from one or the other of two competing strategies: *projection* or *restricted reconstruction*. Projection can be analogized to a well-known formula for adding a point to a principal component analysis. Restricted reconstruction poses a different challenge: how to best approximate redoing the entire multivariate analysis while holding fixed the vector diagram that was previously obtained. This strategy results in a nonlinear optimization problem that can be simplified to a unidimensional search. Various circumstances may warrant either projection or restricted reconstruction.

Principal Graph Encoder Embedding and Principal Community Detection

In this paper, we introduce the concept of principal communities and propose a principal graph encoder embedding method that concurrently detects these communities and achieves vertex embedding. Given a graph adjacency matrix with vertex labels, the method computes a sample community score for each community, ranking them to measure community importance and estimate a set of principal communities. The method then produces a vertex embedding by retaining only the dimensions corresponding to these principal communities. Theoretically, we define the population version of the encoder embedding and the community score based on a random Bernoulli graph distribution. We prove that the population principal graph encoder embedding preserves the conditional density of the vertex labels and that the population community score successfully distinguishes the principal communities. We conduct a variety of simulations to demonstrate the finite-sample accuracy in detecting ground-truth principal communities, as well as the advantages in embedding visualization and subsequent vertex classification. The method is further applied to a set of real-world graphs, showcasing its numerical advantages, including robustness to label noise and computational scalability.

Explaining Categorical Feature Interactions Using Graph Covariance and LLMs

Modern datasets often consist of numerous samples with abundant features and associated timestamps. Analyzing such datasets to uncover underlying events typically requires complex statistical methods and substantial domain expertise. A notable example, and the primary data focus of this paper, is the global synthetic dataset from the Counter Trafficking Data Collaborative (CTDC) -- a global hub of human trafficking data containing over 200,000 anonymized records spanning from 2002 to 2022, with numerous categorical features for each record. In this paper, we propose a fast and scalable method for analyzing and extracting significant categorical feature interactions, and querying large language models (LLMs) to generate data-driven insights that explain these interactions. Our approach begins with a binarization step for categorical features using one-hot encoding, followed by the computation of graph covariance at each time. This graph covariance quantifies temporal changes in dependence structures within categorical data and is established as a consistent dependence measure under the Bernoulli distribution. We use this measure to identify significant feature pairs, such as those with the most frequent trends over time or those exhibiting sudden spikes in dependence at specific moments. These extracted feature pairs, along with their timestamps, are subsequently passed to an LLM tasked with generating potential explanations of the underlying events driving these dependence changes. The effectiveness of our method is demonstrated through extensive simulations, and its application to the CTDC dataset reveals meaningful feature pairs and potential data stories underlying the observed feature interactions.

Investigating social alignment via mirroring in a system of interacting language models

Alignment is a social phenomenon wherein individuals share a common goal or perspective. Mirroring, or mimicking the behaviors and opinions of another individual, is one mechanism by which individuals can become aligned. Large scale investigations of the effect of mirroring on alignment have been limited due to the scalability of traditional experimental designs in sociology. In this paper, we introduce a simple computational framework that enables studying the effect of mirroring behavior on alignment in multi-agent systems. We simulate systems of interacting large language models in this framework and characterize overall system behavior and alignment with quantitative measures of agent dynamics. We find that system behavior is strongly influenced by the range of communication of each agent and that these effects are exacerbated by increased rates of mirroring. We discuss the observed simulated system behavior in the context of known human social dynamics.

Embedding-based statistical inference on generative models

The recent cohort of publicly available generative models can produce human expert level content across a variety of topics and domains. Given a model in this cohort as a base model, methods such as parameter efficient fine-tuning, in-context learning, and constrained decoding have further increased generative capabilities and improved both computational and data efficiency. Entire collections of derivative models have emerged as a byproduct of these methods and each of these models has a set of associated covariates such as a score on a benchmark, an indicator for if the model has (or had) access to sensitive information, etc. that may or may not be available to the user. For some model-level covariates, it is possible to use "similar" models to predict an unknown covariate. In this paper we extend recent results related to embedding-based representations of generative models -- the data kernel perspective space -- to classical statistical inference settings. We demonstrate that using the perspective space as the basis of a notion of "similar" is effective for multiple model-level inference tasks.

Optimizing the Induced Correlation in Omnibus Joint Graph Embeddings

Theoretical and empirical evidence suggests that joint graph embedding algorithms induce correlation across the networks in the embedding space. In the Omnibus joint graph embedding framework, previous results explicitly delineated the dual effects of the algorithm-induced and model-inherent correlations on the correlation across the embedded networks. Accounting for and mitigating the algorithm-induced correlation is key to subsequent inference, as sub-optimal Omnibus matrix constructions have been demonstrated to lead to loss in inference fidelity. This work presents the first efforts to automate the Omnibus construction in order to address two key questions in this joint embedding framework: the correlation-to-OMNI problem and the flat correlation problem. In the flat correlation problem, we seek to understand the minimum algorithm-induced flat correlation (i.e., the same across all graph pairs) produced by a generalized Omnibus embedding. Working in a subspace of the fully general Omnibus matrices, we prove both a lower bound for this flat correlation and that the classical Omnibus construction induces the maximal flat correlation. In the correlation-to-OMNI problem, we present an algorithm -- named corr2Omni -- that, from a given matrix of estimated pairwise graph correlations, estimates the matrix of generalized Omnibus weights that induces optimal correlation in the embedding space. Moreover, in both simulated and real data settings, we demonstrate the increased effectiveness of our corr2Omni algorithm versus the classical Omnibus construction.

Consistent estimation of generative model representations in the data kernel perspective space

Generative models, such as large language models and text-to-image diffusion models, produce relevant information when presented a query. Different models may produce different information when presented the same query. As the landscape of generative models evolves, it is important to develop techniques to study and analyze differences in model behaviour. In this paper we present novel theoretical results for embedding-based representations of generative models in the context of a set of queries. We establish sufficient conditions for the consistent estimation of the model embeddings in situations where the query set and the number of models grow.