Principal Graph Encoder Embedding and Principal Community Detection

In this paper, we introduce the concept of principal communities and propose a principal graph encoder embedding method that concurrently detects these communities and achieves vertex embedding. Given a graph adjacency matrix with vertex labels, the method computes a sample community score for each community, ranking them to measure community importance and estimate a set of principal communities. The method then produces a vertex embedding by retaining only the dimensions corresponding to these principal communities. Theoretically, we define the population version of the encoder embedding and the community score based on a random Bernoulli graph distribution. We prove that the population principal graph encoder embedding preserves the conditional density of the vertex labels and that the population community score successfully distinguishes the principal communities. We conduct a variety of simulations to demonstrate the finite-sample accuracy in detecting ground-truth principal communities, as well as the advantages in embedding visualization and subsequent vertex classification. The method is further applied to a set of real-world graphs, showcasing its numerical advantages, including robustness to label noise and computational scalability.

Embedding-based statistical inference on generative models

The recent cohort of publicly available generative models can produce human expert level content across a variety of topics and domains. Given a model in this cohort as a base model, methods such as parameter efficient fine-tuning, in-context learning, and constrained decoding have further increased generative capabilities and improved both computational and data efficiency. Entire collections of derivative models have emerged as a byproduct of these methods and each of these models has a set of associated covariates such as a score on a benchmark, an indicator for if the model has (or had) access to sensitive information, etc. that may or may not be available to the user. For some model-level covariates, it is possible to use "similar" models to predict an unknown covariate. In this paper we extend recent results related to embedding-based representations of generative models -- the data kernel perspective space -- to classical statistical inference settings. We demonstrate that using the perspective space as the basis of a notion of "similar" is effective for multiple model-level inference tasks.

Tracking the perspectives of interacting language models

Large language models (LLMs) are capable of producing high quality information at unprecedented rates. As these models continue to entrench themselves in society, the content they produce will become increasingly pervasive in databases that are, in turn, incorporated into the pre-training data, fine-tuning data, retrieval data, etc. of other language models. In this paper we formalize the idea of a communication network of LLMs and introduce a method for representing the perspective of individual models within a collection of LLMs. Given these tools we systematically study information diffusion in the communication network of LLMs in various simulated settings.

Semisupervised regression in latent structure networks on unknown manifolds

Random graphs are increasingly becoming objects of interest for modeling networks in a wide range of applications. Latent position random graph models posit that each node is associated with a latent position vector, and that these vectors follow some geometric structure in the latent space. In this paper, we consider random dot product graphs, in which an edge is formed between two nodes with probability given by the inner product of their respective latent positions. We assume that the latent position vectors lie on an unknown one-dimensional curve and are coupled with a response covariate via a regression model. Using the geometry of the underlying latent position vectors, we propose a manifold learning and graph embedding technique to predict the response variable on out-of-sample nodes, and we establish convergence guarantees for these responses. Our theoretical results are supported by simulations and an application to Drosophila brain data.

Discovering Communication Pattern Shifts in Large-Scale Networks using Encoder Embedding and Vertex Dynamics

The analysis of large-scale time-series network data, such as social media and email communications, remains a significant challenge for graph analysis methodology. In particular, the scalability of graph analysis is a critical issue hindering further progress in large-scale downstream inference. In this paper, we introduce a novel approach called "temporal encoder embedding" that can efficiently embed large amounts of graph data with linear complexity. We apply this method to an anonymized time-series communication network from a large organization spanning 2019-2020, consisting of over 100 thousand vertices and 80 million edges. Our method embeds the data within 10 seconds on a standard computer and enables the detection of communication pattern shifts for individual vertices, vertex communities, and the overall graph structure. Through supporting theory and synthesis studies, we demonstrate the theoretical soundness of our approach under random graph models and its numerical effectiveness through simulation studies.

Graph Encoder Ensemble for Simultaneous Vertex Embedding and Community Detection

In this paper we propose a novel and computationally efficient method to simultaneously achieve vertex embedding, community detection, and community size determination. By utilizing a normalized one-hot graph encoder and a new rank-based cluster size measure, the proposed graph encoder ensemble algorithm achieves excellent numerical performance throughout a variety of simulations and real data experiments.

Dynamic Network Sampling for Community Detection

We propose a dynamic network sampling scheme to optimize block recovery for stochastic blockmodel (SBM) in the case where it is prohibitively expensive to observe the entire graph. Theoretically, we provide justification of our proposed Chernoff-optimal dynamic sampling scheme via the Chernoff information. Practically, we evaluate the performance, in terms of block recovery, of our method on several real datasets from different domains. Both theoretically and practically results suggest that our method can identify vertices that have the most impact on block structure so that one can only check whether there are edges between them to save significant resources but still recover the block structure.

An Analysis of Euclidean vs. Graph-Based Framing for Bilingual Lexicon Induction from Word Embedding Spaces

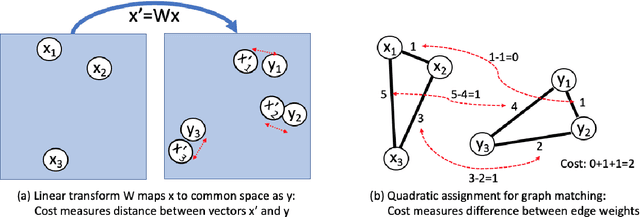
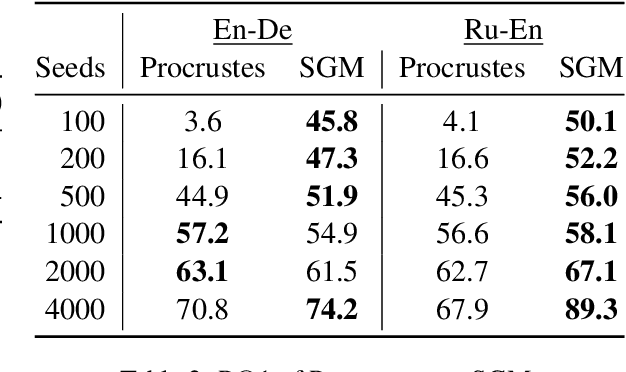
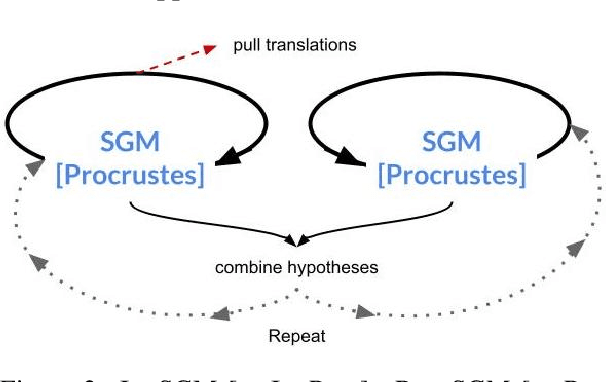
Much recent work in bilingual lexicon induction (BLI) views word embeddings as vectors in Euclidean space. As such, BLI is typically solved by finding a linear transformation that maps embeddings to a common space. Alternatively, word embeddings may be understood as nodes in a weighted graph. This framing allows us to examine a node's graph neighborhood without assuming a linear transform, and exploits new techniques from the graph matching optimization literature. These contrasting approaches have not been compared in BLI so far. In this work, we study the behavior of Euclidean versus graph-based approaches to BLI under differing data conditions and show that they complement each other when combined. We release our code at https://github.com/kellymarchisio/euc-v-graph-bli.

Leveraging semantically similar queries for ranking via combining representations

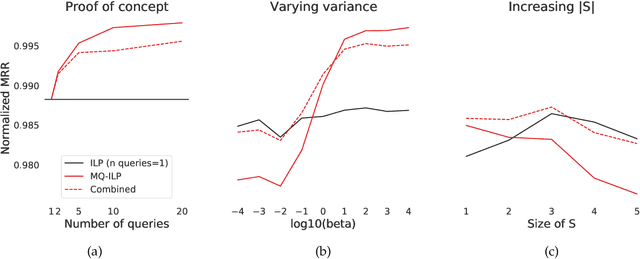
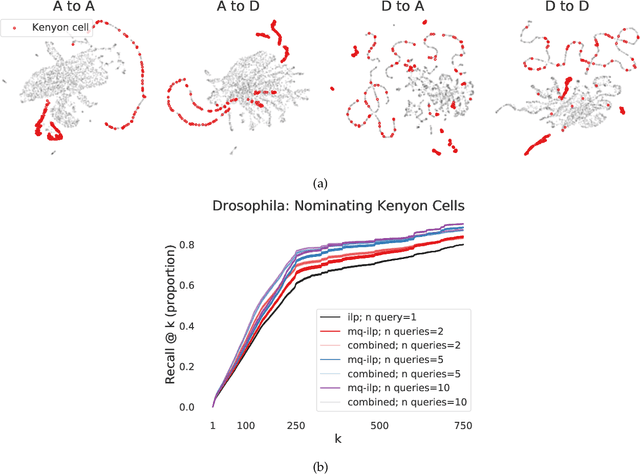
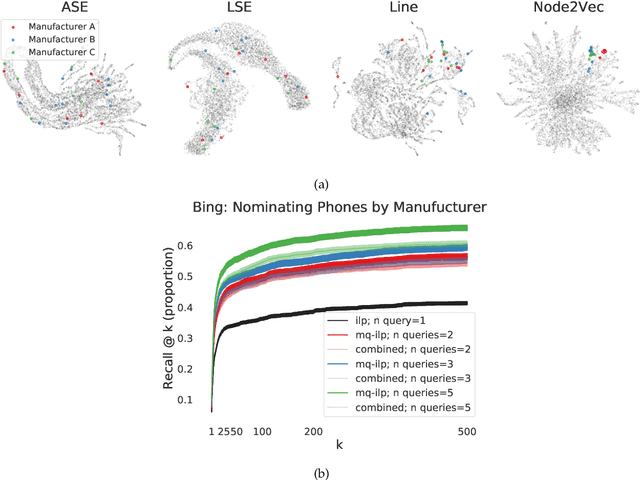
In modern ranking problems, different and disparate representations of the items to be ranked are often available. It is sensible, then, to try to combine these representations to improve ranking. Indeed, learning to rank via combining representations is both principled and practical for learning a ranking function for a particular query. In extremely data-scarce settings, however, the amount of labeled data available for a particular query can lead to a highly variable and ineffective ranking function. One way to mitigate the effect of the small amount of data is to leverage information from semantically similar queries. Indeed, as we demonstrate in simulation settings and real data examples, when semantically similar queries are available it is possible to gainfully use them when ranking with respect to a particular query. We describe and explore this phenomenon in the context of the bias-variance trade off and apply it to the data-scarce settings of a Bing navigational graph and the Drosophila larva connectome.

Dynamic Silos: Modularity in intra-organizational communication networks during the Covid-19 pandemic

Workplace communications around the world were drastically altered by Covid-19, work-from-home orders, and the rise of remote work. We analyze aggregated, anonymized metadata from over 360 billion emails within over 4000 organizations worldwide to examine changes in network community structures from 2019 through 2020. We find that, during 2020, organizations around the world became more siloed, evidenced by increased modularity. This shift was concurrent with decreased stability, indicating that organizational siloes had less stable membership. We provide initial insights into the implications of these network changes -- which we term dynamic silos -- for organizational performance and innovation.