Ali Saad-Eldin
Bilingual Lexicon Induction for Low-Resource Languages using Graph Matching via Optimal Transport
Oct 25, 2022



Abstract:Bilingual lexicons form a critical component of various natural language processing applications, including unsupervised and semisupervised machine translation and crosslingual information retrieval. We improve bilingual lexicon induction performance across 40 language pairs with a graph-matching method based on optimal transport. The method is especially strong with low amounts of supervision.
Graph Matching via Optimal Transport
Nov 09, 2021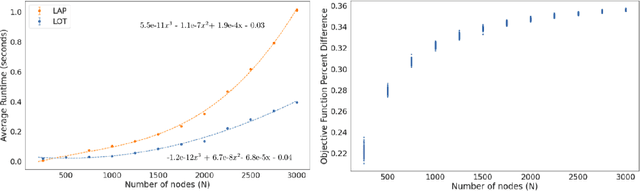
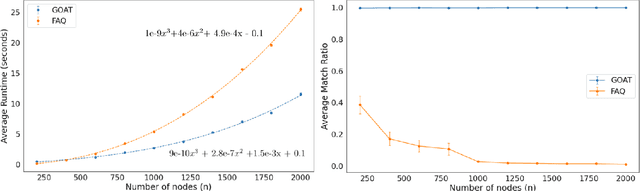
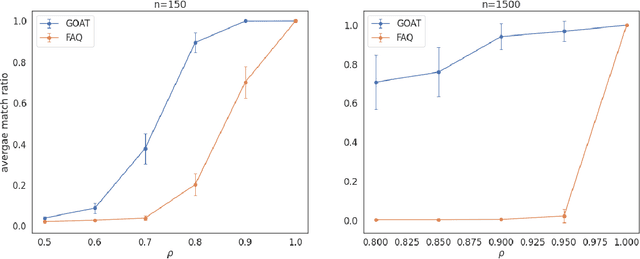
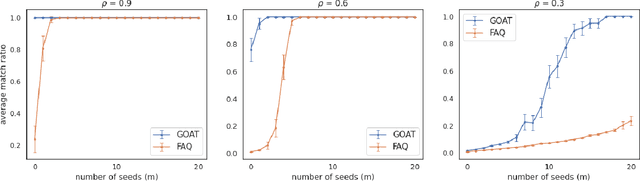
Abstract:The graph matching problem seeks to find an alignment between the nodes of two graphs that minimizes the number of adjacency disagreements. Solving the graph matching is increasingly important due to it's applications in operations research, computer vision, neuroscience, and more. However, current state-of-the-art algorithms are inefficient in matching very large graphs, though they produce good accuracy. The main computational bottleneck of these algorithms is the linear assignment problem, which must be solved at each iteration. In this paper, we leverage the recent advances in the field of optimal transport to replace the accepted use of linear assignment algorithms. We present GOAT, a modification to the state-of-the-art graph matching approximation algorithm "FAQ" (Vogelstein, 2015), replacing its linear sum assignment step with the "Lightspeed Optimal Transport" method of Cuturi (2013). The modification provides improvements to both speed and empirical matching accuracy. The effectiveness of the approach is demonstrated in matching graphs in simulated and real data examples.
An Analysis of Euclidean vs. Graph-Based Framing for Bilingual Lexicon Induction from Word Embedding Spaces
Sep 26, 2021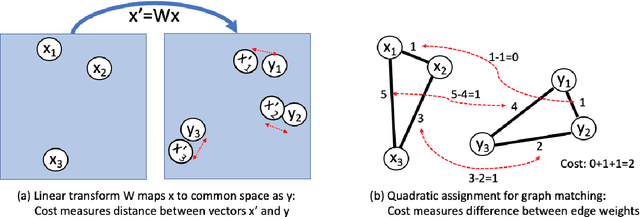

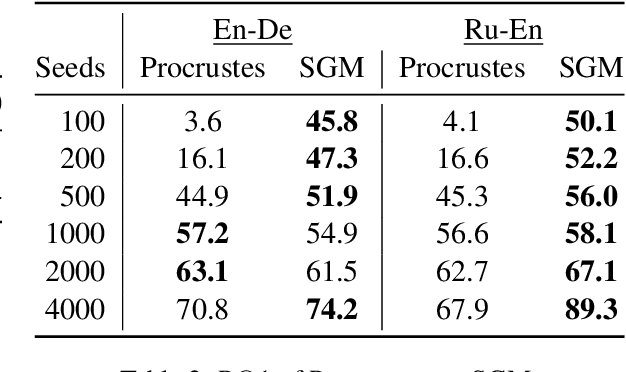
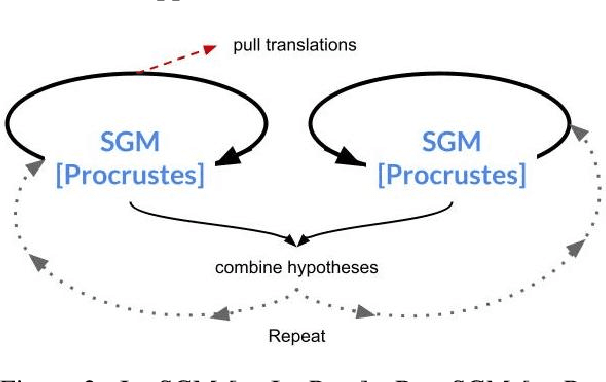
Abstract:Much recent work in bilingual lexicon induction (BLI) views word embeddings as vectors in Euclidean space. As such, BLI is typically solved by finding a linear transformation that maps embeddings to a common space. Alternatively, word embeddings may be understood as nodes in a weighted graph. This framing allows us to examine a node's graph neighborhood without assuming a linear transform, and exploits new techniques from the graph matching optimization literature. These contrasting approaches have not been compared in BLI so far. In this work, we study the behavior of Euclidean versus graph-based approaches to BLI under differing data conditions and show that they complement each other when combined. We release our code at https://github.com/kellymarchisio/euc-v-graph-bli.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge