Carey Priebe
Johns Hopkins University
Edge-Parallel Graph Encoder Embedding
Feb 06, 2024



Abstract:New algorithms for embedding graphs have reduced the asymptotic complexity of finding low-dimensional representations. One-Hot Graph Encoder Embedding (GEE) uses a single, linear pass over edges and produces an embedding that converges asymptotically to the spectral embedding. The scaling and performance benefits of this approach have been limited by a serial implementation in an interpreted language. We refactor GEE into a parallel program in the Ligra graph engine that maps functions over the edges of the graph and uses lock-free atomic instrutions to prevent data races. On a graph with 1.8B edges, this results in a 500 times speedup over the original implementation and a 17 times speedup over a just-in-time compiled version.
Bilingual Lexicon Induction for Low-Resource Languages using Graph Matching via Optimal Transport
Oct 25, 2022



Abstract:Bilingual lexicons form a critical component of various natural language processing applications, including unsupervised and semisupervised machine translation and crosslingual information retrieval. We improve bilingual lexicon induction performance across 40 language pairs with a graph-matching method based on optimal transport. The method is especially strong with low amounts of supervision.
An Analysis of Euclidean vs. Graph-Based Framing for Bilingual Lexicon Induction from Word Embedding Spaces
Sep 26, 2021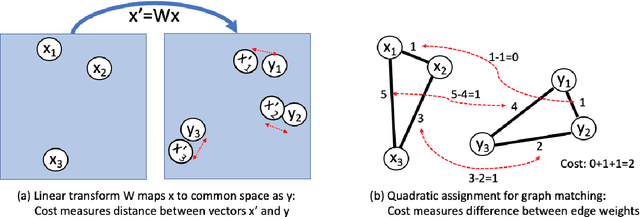

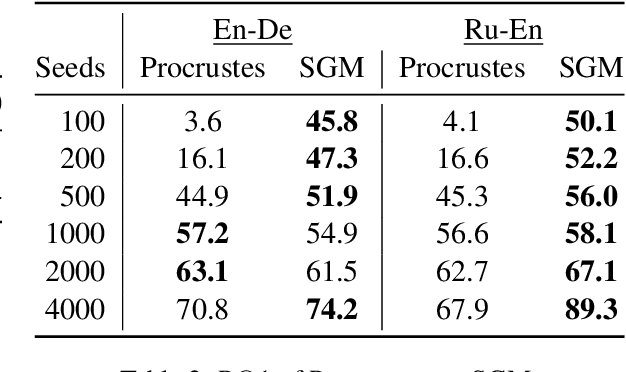
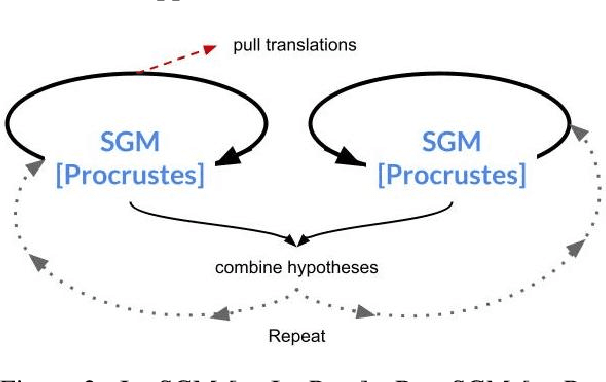
Abstract:Much recent work in bilingual lexicon induction (BLI) views word embeddings as vectors in Euclidean space. As such, BLI is typically solved by finding a linear transformation that maps embeddings to a common space. Alternatively, word embeddings may be understood as nodes in a weighted graph. This framing allows us to examine a node's graph neighborhood without assuming a linear transform, and exploits new techniques from the graph matching optimization literature. These contrasting approaches have not been compared in BLI so far. In this work, we study the behavior of Euclidean versus graph-based approaches to BLI under differing data conditions and show that they complement each other when combined. We release our code at https://github.com/kellymarchisio/euc-v-graph-bli.
Spectral clustering in the weighted stochastic block model
Oct 12, 2019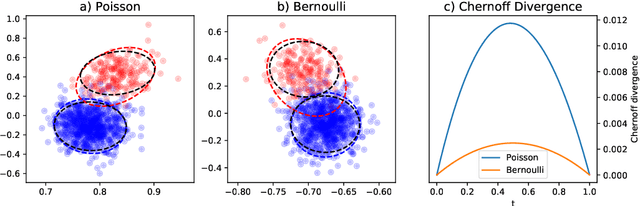
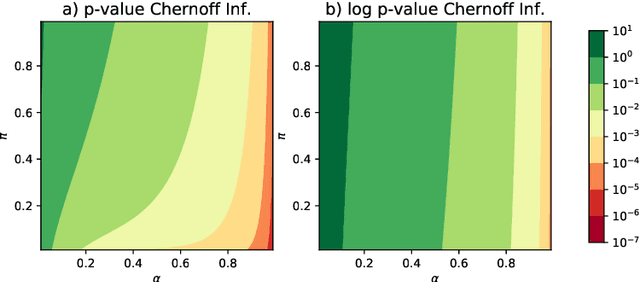
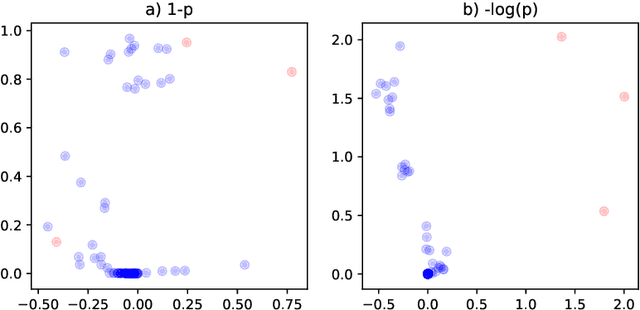
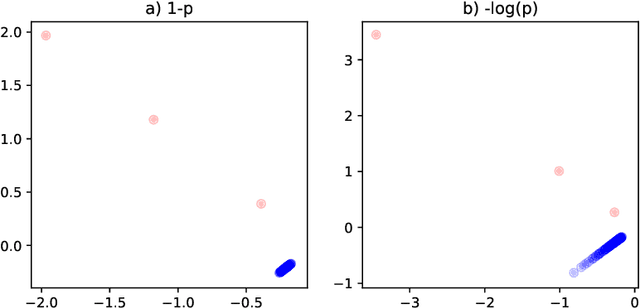
Abstract:This paper is concerned with the statistical analysis of a real-valued symmetric data matrix. We assume a weighted stochastic block model: the matrix indices, taken to represent nodes, can be partitioned into communities so that all entries corresponding to a given community pair are replicates of the same random variable. Extending results previously known only for unweighted graphs, we provide a limit theorem showing that the point cloud obtained from spectrally embedding the data matrix follows a Gaussian mixture model where each community is represented with an elliptical component. We can therefore formally evaluate how well the communities separate under different data transformations, for example, whether it is productive to "take logs". We find that performance is invariant to affine transformation of the entries, but this expected and desirable feature hinges on adaptively selecting the eigenvectors according to eigenvalue magnitude and using Gaussian clustering. We present a network anomaly detection problem with cyber-security data where the matrix of log p-values, as opposed to p-values, has both theoretical and empirical advantages.
Vertex Classification on Weighted Networks
Jun 07, 2019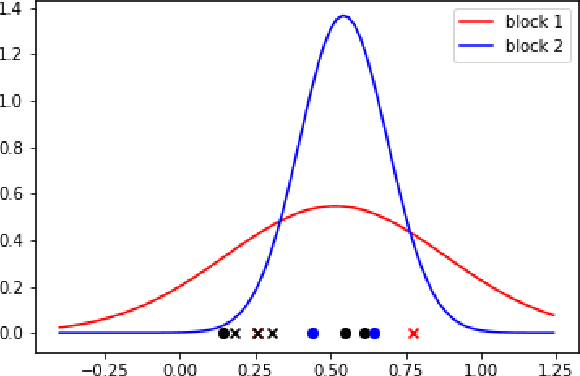

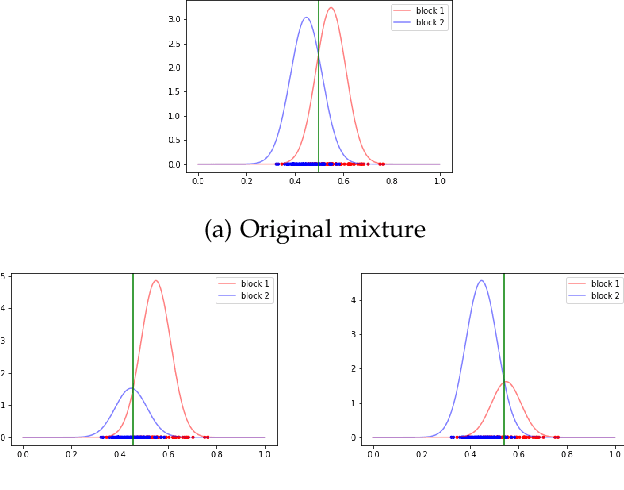
Abstract:This paper proposes a discrimination technique for vertices in a weighted network. We assume that the edge weights and adjacencies in the network are conditionally independent and that both sources of information encode class membership information. In particular, we introduce a edge weight distribution matrix to the standard K-Block Stochastic Block Model to model weighted networks. This allows us to develop simple yet powerful extensions of classification techniques using the spectral embedding of the unweighted adjacency matrix. We consider two assumptions on the edge weight distributions and propose classification procedures in both settings. We show the effectiveness of the proposed classifiers by comparing them to quadratic discriminant analysis following the spectral embedding of a transformed weighted network. Moreover, we discuss and show how the methods perform when the edge weights do not encode class membership information.
Sparse Representation Classification via Screening for Graphs
Jun 04, 2019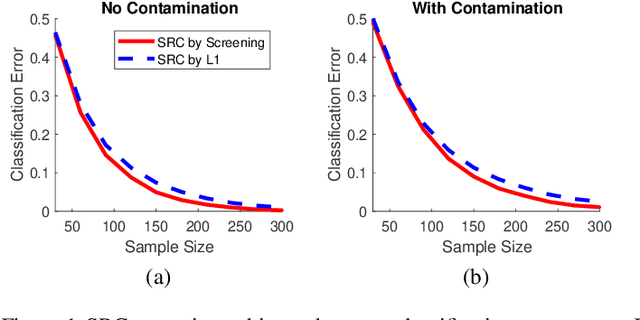


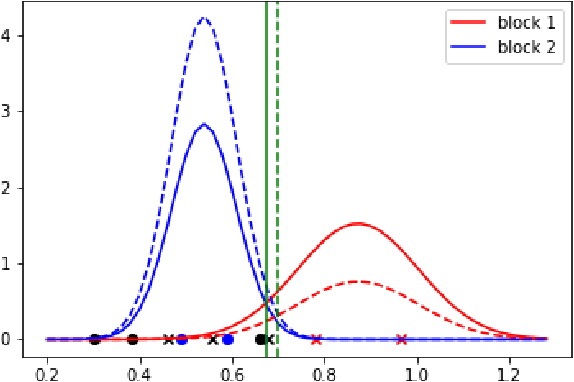
Abstract:The sparse representation classifier (SRC) is shown to work well for image recognition problems that satisfy a subspace assumption. In this paper we propose a new implementation of SRC via screening, establish its equivalence to the original SRC under regularity conditions, and prove its classification consistency for random graphs drawn from stochastic blockmodels. The results are demonstrated via simulations and real data experiments, where the new algorithm achieves comparable numerical performance but significantly faster.
Vertex nomination: The canonical sampling and the extended spectral nomination schemes
Feb 14, 2018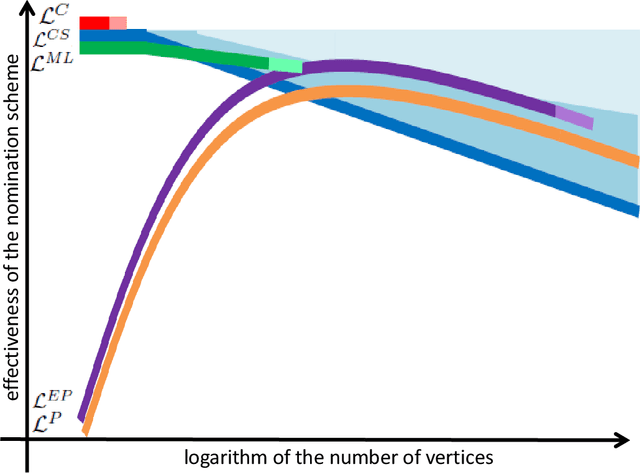
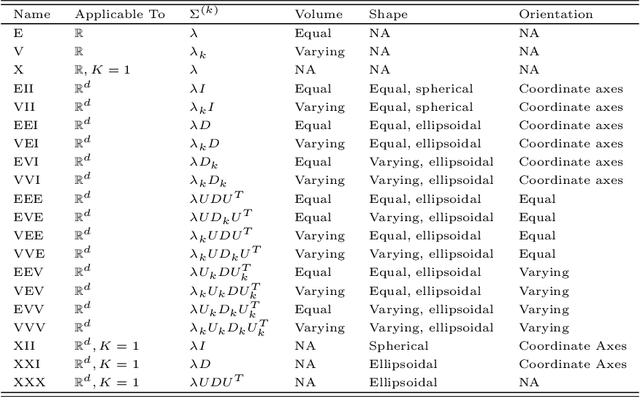
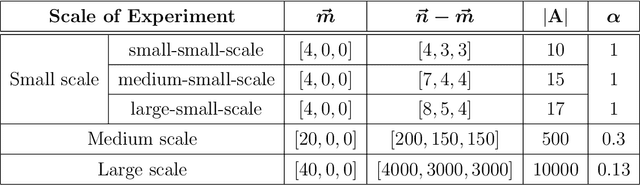
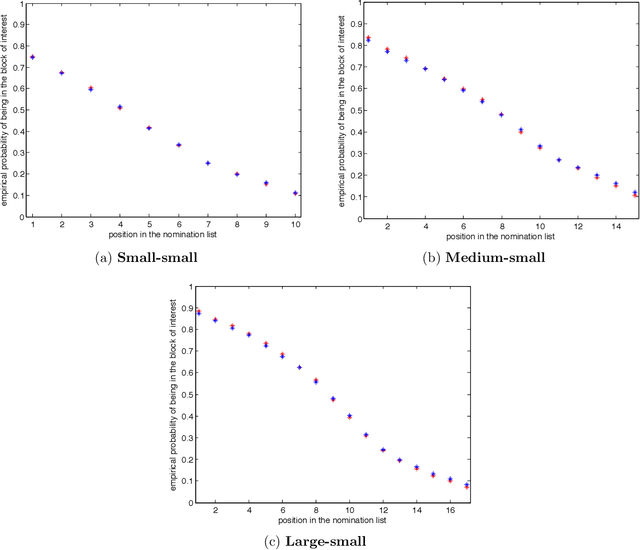
Abstract:Suppose that one particular block in a stochastic block model is deemed "interesting," but block labels are only observed for a few of the vertices. Utilizing a graph realized from the model, the vertex nomination task is to order the vertices with unobserved block labels into a "nomination list" with the goal of having an abundance of interesting vertices near the top of the list. In this paper we extend and enhance two basic vertex nomination schemes; the canonical nomination scheme ${\mathcal L}^C$ and the spectral partitioning nomination scheme ${\mathcal L}^P$. The canonical nomination scheme ${\mathcal L}^C$ is provably optimal, but is computationally intractable, being impractical to implement even on modestly sized graphs. With this in mind, we introduce a scalable, Markov chain Monte Carlo-based nomination scheme, called the {\it canonical sampling nomination scheme} ${\mathcal L}^{CS}$, that converges to the canonical nomination scheme ${\mathcal L}^{C}$ as the amount of sampling goes to infinity. We also introduce a novel spectral partitioning nomination scheme called the {\it extended spectral partitioning nomination scheme} ${\mathcal L}^{EP}$. Real-data and simulation experiments are employed to illustrate the effectiveness of these vertex nomination schemes, as well as their empirical computational complexity.
Robust Vertex Classification
Apr 22, 2015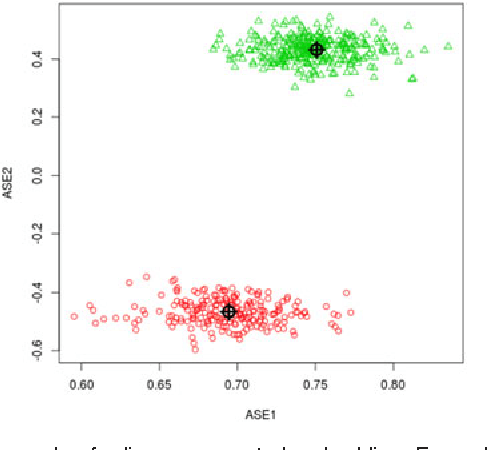
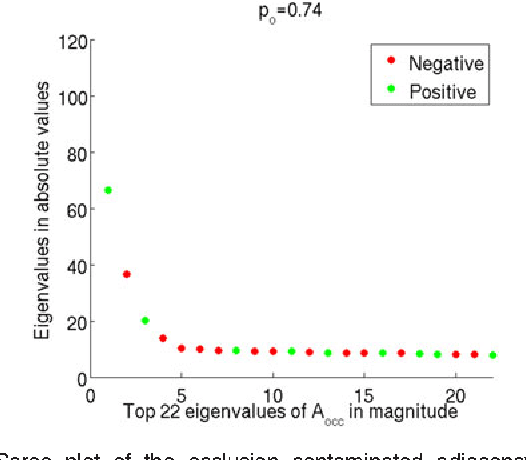
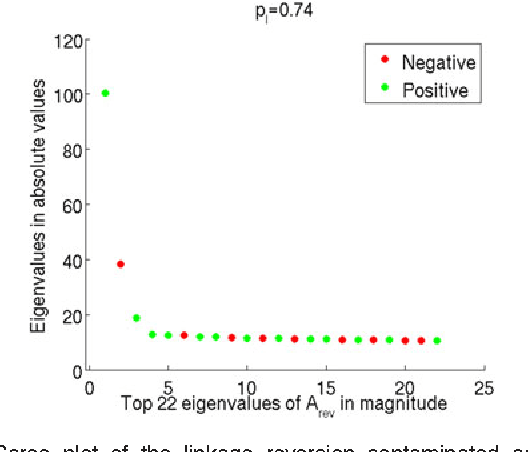
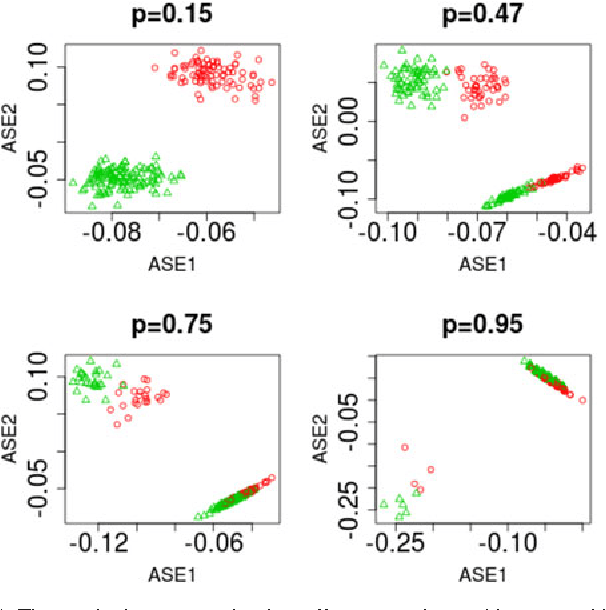
Abstract:For random graphs distributed according to stochastic blockmodels, a special case of latent position graphs, adjacency spectral embedding followed by appropriate vertex classification is asymptotically Bayes optimal; but this approach requires knowledge of and critically depends on the model dimension. In this paper, we propose a sparse representation vertex classifier which does not require information about the model dimension. This classifier represents a test vertex as a sparse combination of the vertices in the training set and uses the recovered coefficients to classify the test vertex. We prove consistency of our proposed classifier for stochastic blockmodels, and demonstrate that the sparse representation classifier can predict vertex labels with higher accuracy than adjacency spectral embedding approaches via both simulation studies and real data experiments. Our results demonstrate the robustness and effectiveness of our proposed vertex classifier when the model dimension is unknown.
Perfect Clustering for Stochastic Blockmodel Graphs via Adjacency Spectral Embedding
Jan 15, 2015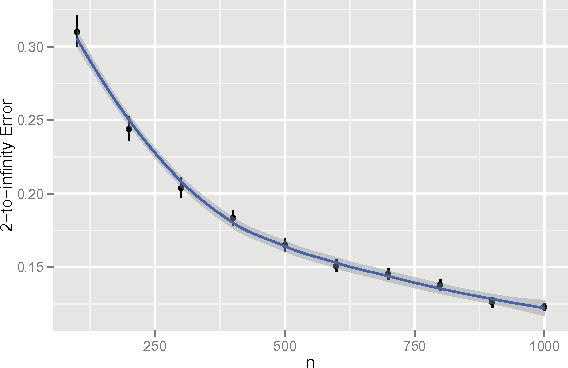
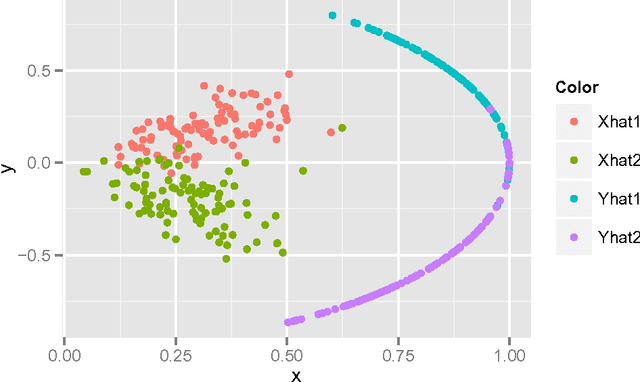
Abstract:Vertex clustering in a stochastic blockmodel graph has wide applicability and has been the subject of extensive research. In thispaper, we provide a short proof that the adjacency spectral embedding can be used to obtain perfect clustering for the stochastic blockmodel and the degree-corrected stochastic blockmodel. We also show an analogous result for the more general random dot product graph model.
* 22 pages, including references; 2 figures
Techniques for clustering interaction data as a collection of graphs
Jan 10, 2015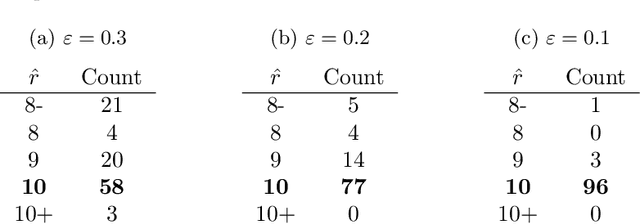

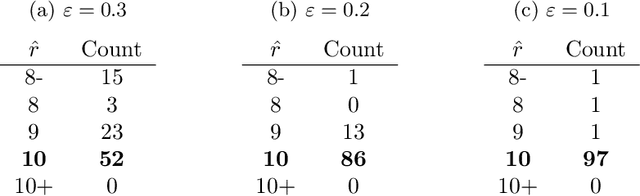

Abstract:A natural approach to analyze interaction data of form "what-connects-to-what-when" is to create a time-series (or rather a sequence) of graphs through temporal discretization (bandwidth selection) and spatial discretization (vertex contraction). Such discretization together with non-negative factorization techniques can be useful for obtaining clustering of graphs. Motivating application of performing clustering of graphs (as opposed to vertex clustering) can be found in neuroscience and in social network analysis, and it can also be used to enhance community detection (i.e., vertex clustering) by way of conditioning on the cluster labels. In this paper, we formulate a problem of clustering of graphs as a model selection problem. Our approach involves information criteria, non-negative matrix factorization and singular value thresholding, and we illustrate our techniques using real and simulated data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge