Valid Conformal Prediction for Dynamic GNNs

Graph neural networks (GNNs) are powerful black-box models which have shown impressive empirical performance. However, without any form of uncertainty quantification, it can be difficult to trust such models in high-risk scenarios. Conformal prediction aims to address this problem, however, an assumption of exchangeability is required for its validity which has limited its applicability to static graphs and transductive regimes. We propose to use unfolding, which allows any existing static GNN to output a dynamic graph embedding with exchangeability properties. Using this, we extend the validity of conformal prediction to dynamic GNNs in both transductive and semi-inductive regimes. We provide a theoretical guarantee of valid conformal prediction in these cases and demonstrate the empirical validity, as well as the performance gains, of unfolded GNNs against standard GNN architectures on both simulated and real datasets.

A Simple and Powerful Framework for Stable Dynamic Network Embedding

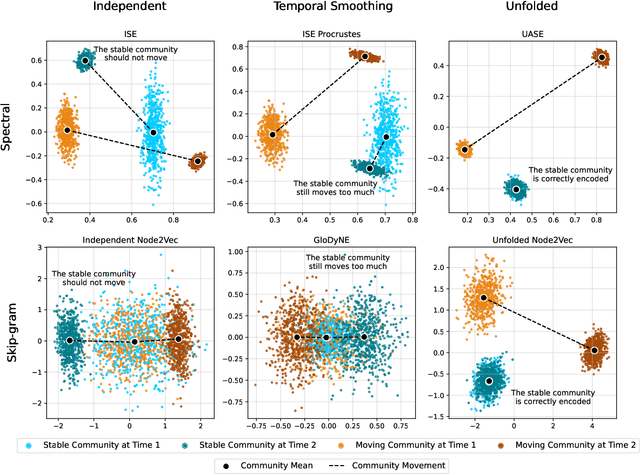
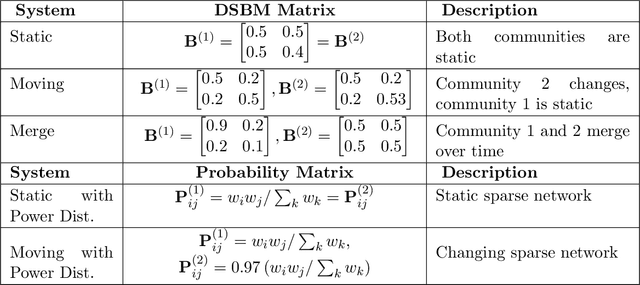
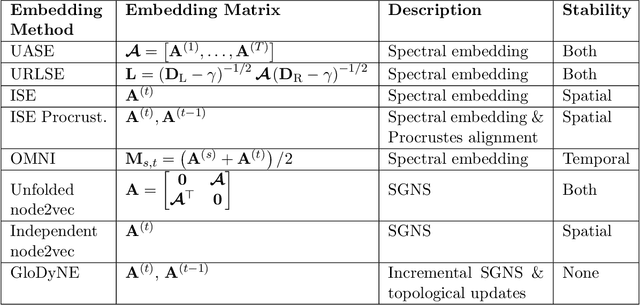
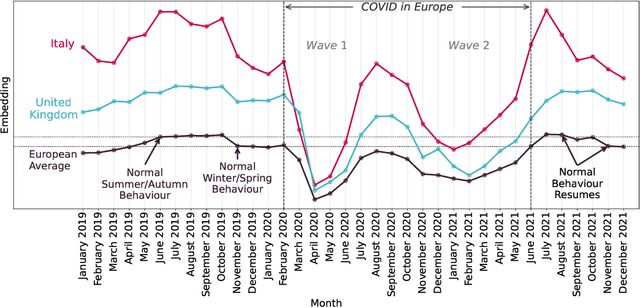
In this paper, we address the problem of dynamic network embedding, that is, representing the nodes of a dynamic network as evolving vectors within a low-dimensional space. While the field of static network embedding is wide and established, the field of dynamic network embedding is comparatively in its infancy. We propose that a wide class of established static network embedding methods can be used to produce interpretable and powerful dynamic network embeddings when they are applied to the dilated unfolded adjacency matrix. We provide a theoretical guarantee that, regardless of embedding dimension, these unfolded methods will produce stable embeddings, meaning that nodes with identical latent behaviour will be exchangeable, regardless of their position in time or space. We additionally define a hypothesis testing framework which can be used to evaluate the quality of a dynamic network embedding by testing for planted structure in simulated networks. Using this, we demonstrate that, even in trivial cases, unstable methods are often either conservative or encode incorrect structure. In contrast, we demonstrate that our suite of stable unfolded methods are not only more interpretable but also more powerful in comparison to their unstable counterparts.

Intensity Profile Projection: A Framework for Continuous-Time Representation Learning for Dynamic Networks

We present a new algorithmic framework, Intensity Profile Projection, for learning continuous-time representations of the nodes of a dynamic network, characterised by a node set and a collection of instantaneous interaction events which occur in continuous time. Our framework consists of three stages: estimating the intensity functions underlying the interactions between pairs of nodes, e.g. via kernel smoothing; learning a projection which minimises a notion of intensity reconstruction error; and inductively constructing evolving node representations via the learned projection. We show that our representations preserve the underlying structure of the network, and are temporally coherent, meaning that node representations can be meaningfully compared at different points in time. We develop estimation theory which elucidates the role of smoothing as a bias-variance trade-off, and shows how we can reduce smoothing as the signal-to-noise ratio increases on account of the algorithm `borrowing strength' across the network.

Hierarchical clustering with dot products recovers hidden tree structure

In this paper we offer a new perspective on the well established agglomerative clustering algorithm, focusing on recovery of hierarchical structure. We recommend a simple variant of the standard algorithm, in which clusters are merged by maximum average dot product and not, for example, by minimum distance or within-cluster variance. We demonstrate that the tree output by this algorithm provides a bona fide estimate of generative hierarchical structure in data, under a generic probabilistic graphical model. The key technical innovations are to understand how hierarchical information in this model translates into tree geometry which can be recovered from data, and to characterise the benefits of simultaneously growing sample size and data dimension. We demonstrate superior tree recovery performance with real data over existing approaches such as UPGMA, Ward's method, and HDBSCAN.

Implications of sparsity and high triangle density for graph representation learning

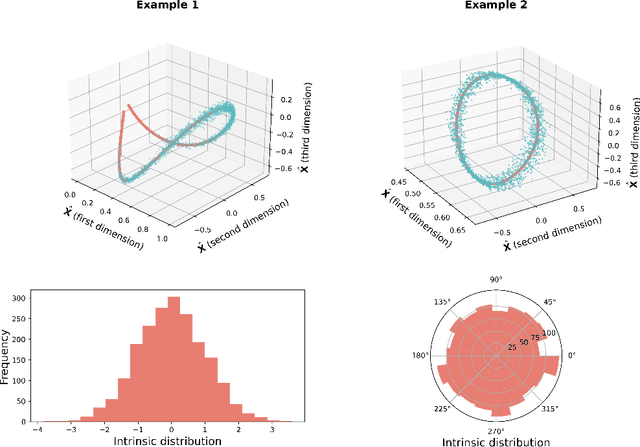
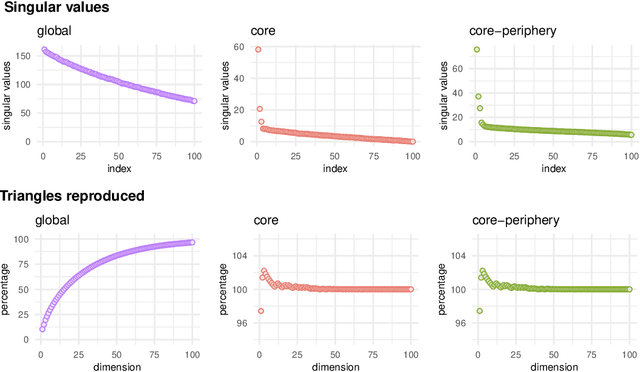
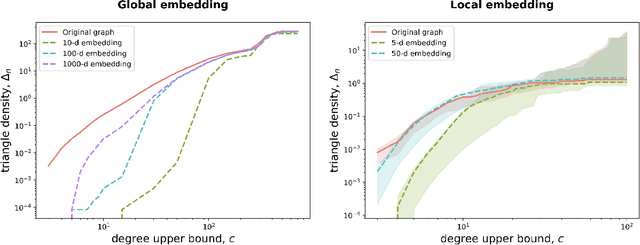
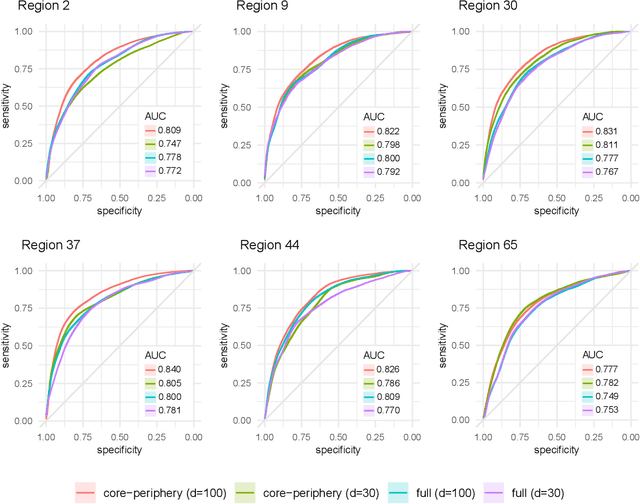
Recent work has shown that sparse graphs containing many triangles cannot be reproduced using a finite-dimensional representation of the nodes, in which link probabilities are inner products. Here, we show that such graphs can be reproduced using an infinite-dimensional inner product model, where the node representations lie on a low-dimensional manifold. Recovering a global representation of the manifold is impossible in a sparse regime. However, we can zoom in on local neighbourhoods, where a lower-dimensional representation is possible. As our constructions allow the points to be uniformly distributed on the manifold, we find evidence against the common perception that triangles imply community structure.

Spectral embedding and the latent geometry of multipartite networks

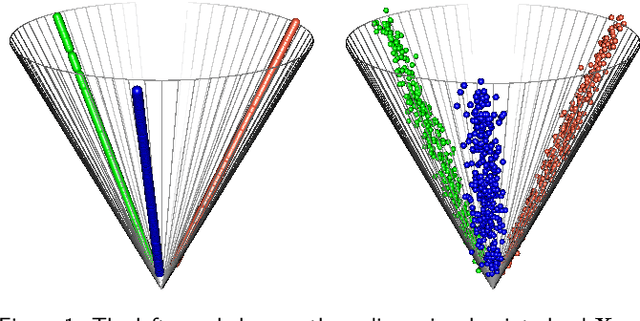
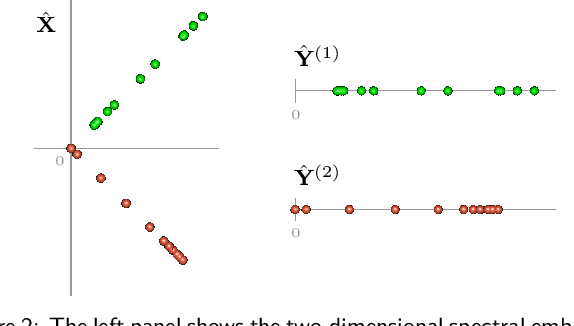
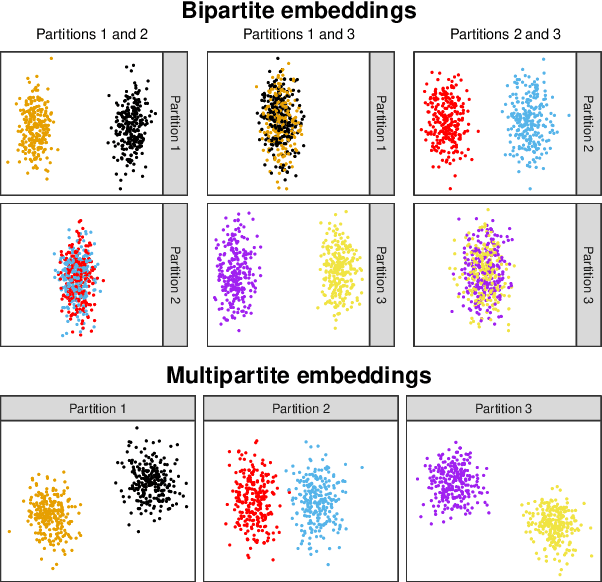
Spectral embedding finds vector representations of the nodes of a network, based on the eigenvectors of its adjacency or Laplacian matrix, and has found applications throughout the sciences. Many such networks are multipartite, meaning their nodes can be divided into partitions and nodes of the same partition are never connected. When the network is multipartite, this paper demonstrates that the node representations obtained via spectral embedding live near partition-specific low-dimensional subspaces of a higher-dimensional ambient space. For this reason we propose a follow-on step after spectral embedding, to recover node representations in their intrinsic rather than ambient dimension, proving uniform consistency under a low-rank, inhomogeneous random graph model. Our method naturally generalizes bipartite spectral embedding, in which node representations are obtained by singular value decomposition of the biadjacency or bi-Laplacian matrix.

Spectral embedding for dynamic networks with stability guarantees

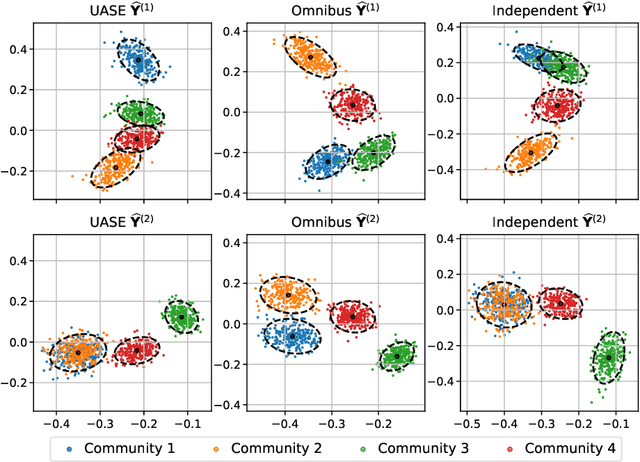
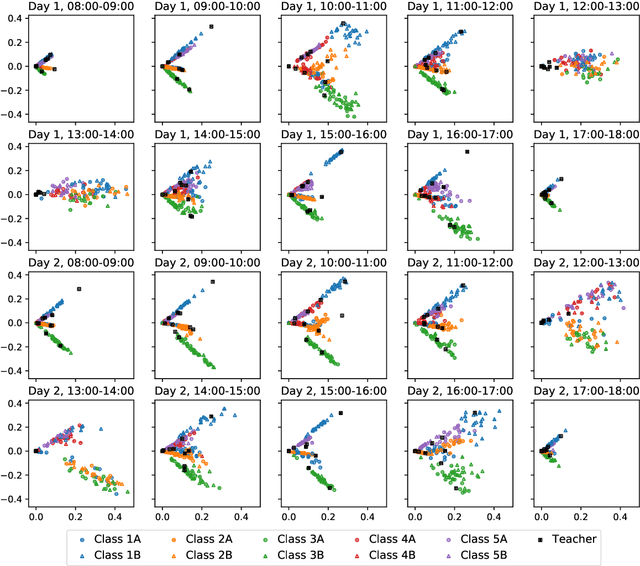
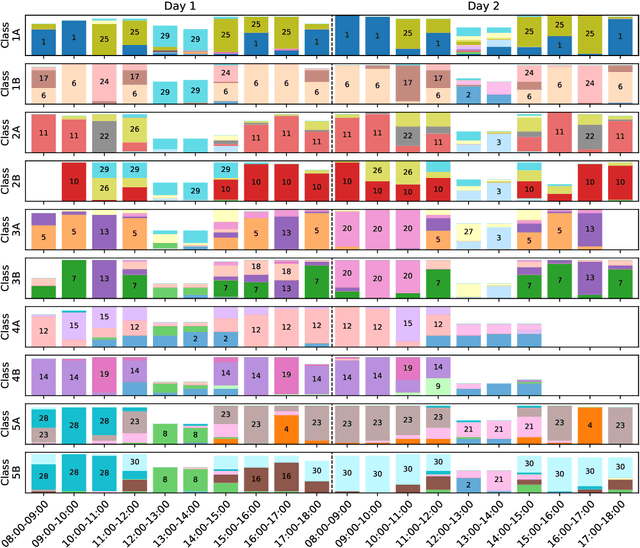
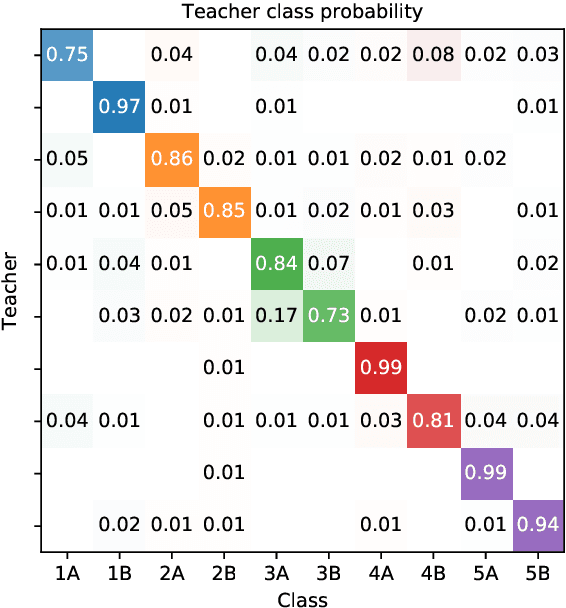
We consider the problem of embedding a dynamic network, to obtain time-evolving vector representations of each node, which can then be used to describe the changes in behaviour of a single node, one or more communities, or the entire graph. Given this open-ended remit, we wish to guarantee stability in the spatio-temporal positioning of the nodes: assigning the same position, up to noise, to nodes behaving similarly at a given time (cross-sectional stability) and a constant position, up to noise, to a single node behaving similarly across different times (longitudinal stability). These properties are defined formally within a generic dynamic latent position model. By showing how this model can be recast as a multilayer random dot product graph, we demonstrate that unfolded adjacency spectral embedding satisfies both stability conditions, allowing, for example, spatio-temporal clustering under the dynamic stochastic block model. We also show how alternative methods, such as omnibus, independent or time-averaged spectral embedding, lack one or the other form of stability.

Matrix factorisation and the interpretation of geodesic distance

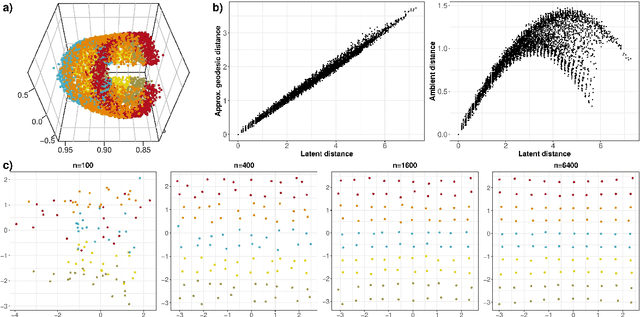
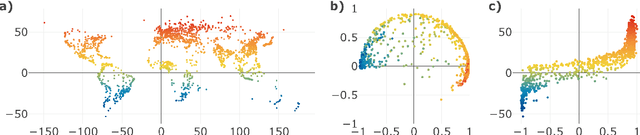
Given a graph or similarity matrix, we consider the problem of recovering a notion of true distance between the nodes, and so their true positions. Through new insights into the manifold geometry underlying a generic latent position model, we show that this can be accomplished in two steps: matrix factorisation, followed by nonlinear dimension reduction. This combination is effective because the point cloud obtained in the first step lives close to a manifold in which latent distance is encoded as geodesic distance. Hence, a nonlinear dimension reduction tool, approximating geodesic distance, can recover the latent positions, up to a simple transformation. We give a detailed account of the case where spectral embedding is used, followed by Isomap, and provide encouraging experimental evidence for other combinations of techniques.

Spectral clustering under degree heterogeneity: a case for the random walk Laplacian

This paper shows that graph spectral embedding using the random walk Laplacian produces vector representations which are completely corrected for node degree. Under a generalised random dot product graph, the embedding provides uniformly consistent estimates of degree-corrected latent positions, with asymptotically Gaussian error. In the special case of a degree-corrected stochastic block model, the embedding concentrates about K distinct points, representing communities. These can be recovered perfectly, asymptotically, through a subsequent clustering step, without spherical projection, as commonly required by algorithms based on the adjacency or normalised, symmetric Laplacian matrices. While the estimand does not depend on degree, the asymptotic variance of its estimate does -- higher degree nodes are embedded more accurately than lower degree nodes. Our central limit theorem therefore suggests fitting a weighted Gaussian mixture model as the subsequent clustering step, for which we provide an expectation-maximisation algorithm.

Spectral clustering on spherical coordinates under the degree-corrected stochastic blockmodel

Spectral clustering is a popular method for community detection in networks under the assumption of the standard stochastic blockmodel. Taking a matrix representation of the graph such as the adjacency matrix, the nodes are clustered on a low dimensional projection obtained from a truncated spectral decomposition of the matrix. Estimating the number of communities and the dimension of the reduced latent space well is crucial for good performance of spectral clustering algorithms. Real-world networks, such as computer networks studied in cyber-security applications, often present heterogeneous within-community degree distributions which are better addressed by the degree-corrected stochastic blockmodel. A novel, model-based method is proposed in this article for simultaneous and automated selection of the number of communities and latent dimension for spectral clustering under the degree-corrected stochastic blockmodel. The method is based on a transformation to spherical coordinates of the spectral embedding, and on a novel modelling assumption in the transformed space, which is then embedded into an existing model selection framework for estimating the number of communities and the latent dimension. Results show improved performance over competing methods on simulated and real-world computer network data.