Hierarchical clustering with dot products recovers hidden tree structure

In this paper we offer a new perspective on the well established agglomerative clustering algorithm, focusing on recovery of hierarchical structure. We recommend a simple variant of the standard algorithm, in which clusters are merged by maximum average dot product and not, for example, by minimum distance or within-cluster variance. We demonstrate that the tree output by this algorithm provides a bona fide estimate of generative hierarchical structure in data, under a generic probabilistic graphical model. The key technical innovations are to understand how hierarchical information in this model translates into tree geometry which can be recovered from data, and to characterise the benefits of simultaneously growing sample size and data dimension. We demonstrate superior tree recovery performance with real data over existing approaches such as UPGMA, Ward's method, and HDBSCAN.

Matrix factorisation and the interpretation of geodesic distance

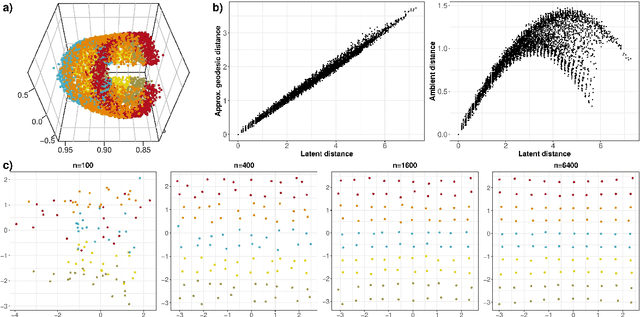
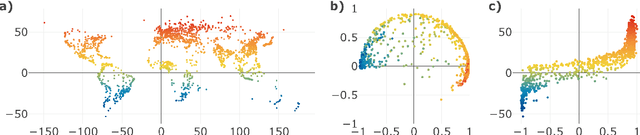
Given a graph or similarity matrix, we consider the problem of recovering a notion of true distance between the nodes, and so their true positions. Through new insights into the manifold geometry underlying a generic latent position model, we show that this can be accomplished in two steps: matrix factorisation, followed by nonlinear dimension reduction. This combination is effective because the point cloud obtained in the first step lives close to a manifold in which latent distance is encoded as geodesic distance. Hence, a nonlinear dimension reduction tool, approximating geodesic distance, can recover the latent positions, up to a simple transformation. We give a detailed account of the case where spectral embedding is used, followed by Isomap, and provide encouraging experimental evidence for other combinations of techniques.