The Origins of Representation Manifolds in Large Language Models

There is a large ongoing scientific effort in mechanistic interpretability to map embeddings and internal representations of AI systems into human-understandable concepts. A key element of this effort is the linear representation hypothesis, which posits that neural representations are sparse linear combinations of `almost-orthogonal' direction vectors, reflecting the presence or absence of different features. This model underpins the use of sparse autoencoders to recover features from representations. Moving towards a fuller model of features, in which neural representations could encode not just the presence but also a potentially continuous and multidimensional value for a feature, has been a subject of intense recent discourse. We describe why and how a feature might be represented as a manifold, demonstrating in particular that cosine similarity in representation space may encode the intrinsic geometry of a feature through shortest, on-manifold paths, potentially answering the question of how distance in representation space and relatedness in concept space could be connected. The critical assumptions and predictions of the theory are validated on text embeddings and token activations of large language models.

Entrywise error bounds for low-rank approximations of kernel matrices

In this paper, we derive entrywise error bounds for low-rank approximations of kernel matrices obtained using the truncated eigen-decomposition (or singular value decomposition). While this approximation is well-known to be optimal with respect to the spectral and Frobenius norm error, little is known about the statistical behaviour of individual entries. Our error bounds fill this gap. A key technical innovation is a delocalisation result for the eigenvectors of the kernel matrix corresponding to small eigenvalues, which takes inspiration from the field of Random Matrix Theory. Finally, we validate our theory with an empirical study of a collection of synthetic and real-world datasets.

Intensity Profile Projection: A Framework for Continuous-Time Representation Learning for Dynamic Networks

We present a new algorithmic framework, Intensity Profile Projection, for learning continuous-time representations of the nodes of a dynamic network, characterised by a node set and a collection of instantaneous interaction events which occur in continuous time. Our framework consists of three stages: estimating the intensity functions underlying the interactions between pairs of nodes, e.g. via kernel smoothing; learning a projection which minimises a notion of intensity reconstruction error; and inductively constructing evolving node representations via the learned projection. We show that our representations preserve the underlying structure of the network, and are temporally coherent, meaning that node representations can be meaningfully compared at different points in time. We develop estimation theory which elucidates the role of smoothing as a bias-variance trade-off, and shows how we can reduce smoothing as the signal-to-noise ratio increases on account of the algorithm `borrowing strength' across the network.

Hierarchical clustering with dot products recovers hidden tree structure

In this paper we offer a new perspective on the well established agglomerative clustering algorithm, focusing on recovery of hierarchical structure. We recommend a simple variant of the standard algorithm, in which clusters are merged by maximum average dot product and not, for example, by minimum distance or within-cluster variance. We demonstrate that the tree output by this algorithm provides a bona fide estimate of generative hierarchical structure in data, under a generic probabilistic graphical model. The key technical innovations are to understand how hierarchical information in this model translates into tree geometry which can be recovered from data, and to characterise the benefits of simultaneously growing sample size and data dimension. We demonstrate superior tree recovery performance with real data over existing approaches such as UPGMA, Ward's method, and HDBSCAN.

Implications of sparsity and high triangle density for graph representation learning

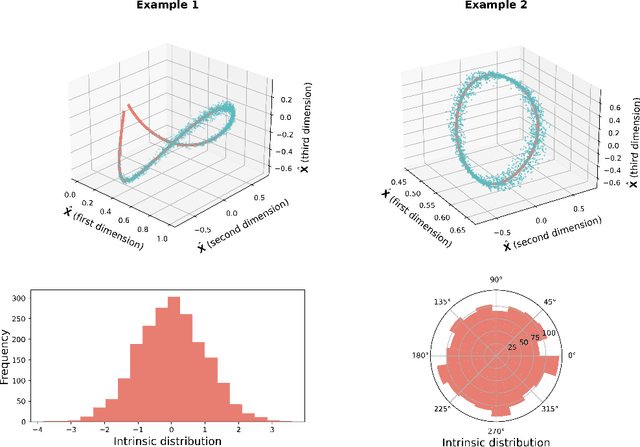
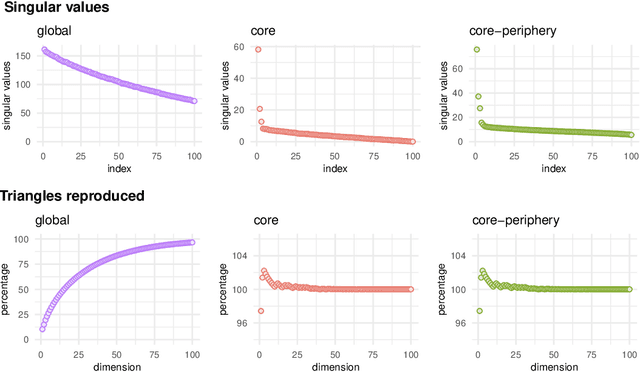
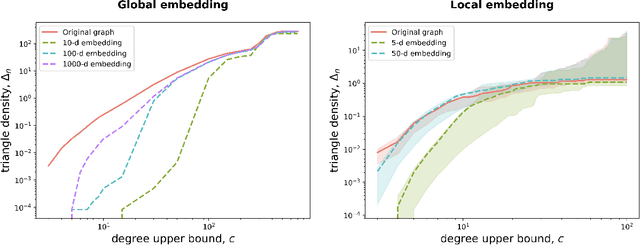
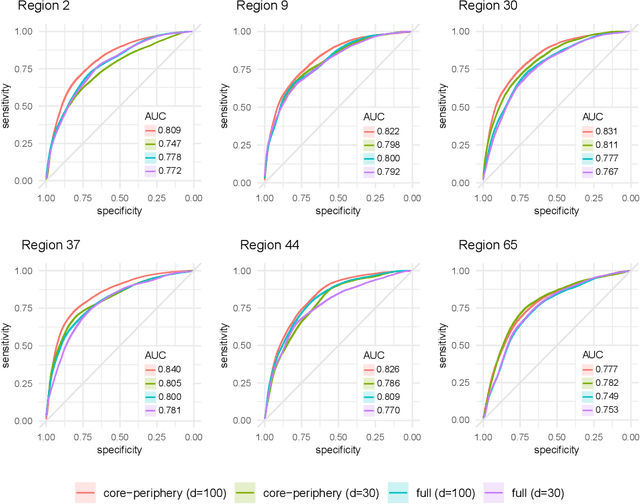
Recent work has shown that sparse graphs containing many triangles cannot be reproduced using a finite-dimensional representation of the nodes, in which link probabilities are inner products. Here, we show that such graphs can be reproduced using an infinite-dimensional inner product model, where the node representations lie on a low-dimensional manifold. Recovering a global representation of the manifold is impossible in a sparse regime. However, we can zoom in on local neighbourhoods, where a lower-dimensional representation is possible. As our constructions allow the points to be uniformly distributed on the manifold, we find evidence against the common perception that triangles imply community structure.

Spectral embedding and the latent geometry of multipartite networks

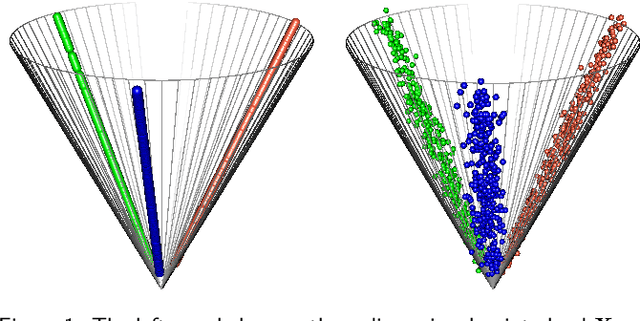
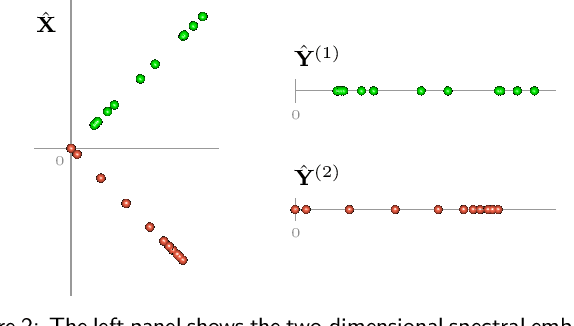
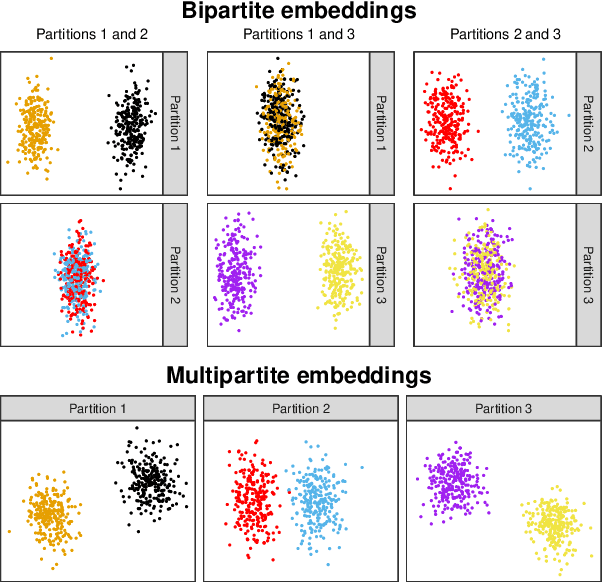
Spectral embedding finds vector representations of the nodes of a network, based on the eigenvectors of its adjacency or Laplacian matrix, and has found applications throughout the sciences. Many such networks are multipartite, meaning their nodes can be divided into partitions and nodes of the same partition are never connected. When the network is multipartite, this paper demonstrates that the node representations obtained via spectral embedding live near partition-specific low-dimensional subspaces of a higher-dimensional ambient space. For this reason we propose a follow-on step after spectral embedding, to recover node representations in their intrinsic rather than ambient dimension, proving uniform consistency under a low-rank, inhomogeneous random graph model. Our method naturally generalizes bipartite spectral embedding, in which node representations are obtained by singular value decomposition of the biadjacency or bi-Laplacian matrix.

Spectral clustering under degree heterogeneity: a case for the random walk Laplacian

This paper shows that graph spectral embedding using the random walk Laplacian produces vector representations which are completely corrected for node degree. Under a generalised random dot product graph, the embedding provides uniformly consistent estimates of degree-corrected latent positions, with asymptotically Gaussian error. In the special case of a degree-corrected stochastic block model, the embedding concentrates about K distinct points, representing communities. These can be recovered perfectly, asymptotically, through a subsequent clustering step, without spherical projection, as commonly required by algorithms based on the adjacency or normalised, symmetric Laplacian matrices. While the estimand does not depend on degree, the asymptotic variance of its estimate does -- higher degree nodes are embedded more accurately than lower degree nodes. Our central limit theorem therefore suggests fitting a weighted Gaussian mixture model as the subsequent clustering step, for which we provide an expectation-maximisation algorithm.