Unsupervised Attributed Dynamic Network Embedding with Stability Guarantees

Stability for dynamic network embeddings ensures that nodes behaving the same at different times receive the same embedding, allowing comparison of nodes in the network across time. We present attributed unfolded adjacency spectral embedding (AUASE), a stable unsupervised representation learning framework for dynamic networks in which nodes are attributed with time-varying covariate information. To establish stability, we prove uniform convergence to an associated latent position model. We quantify the benefits of our dynamic embedding by comparing with state-of-the-art network representation learning methods on three real attributed networks. To the best of our knowledge, AUASE is the only attributed dynamic embedding that satisfies stability guarantees without the need for ground truth labels, which we demonstrate provides significant improvements for link prediction and node classification.

Valid Conformal Prediction for Dynamic GNNs

Graph neural networks (GNNs) are powerful black-box models which have shown impressive empirical performance. However, without any form of uncertainty quantification, it can be difficult to trust such models in high-risk scenarios. Conformal prediction aims to address this problem, however, an assumption of exchangeability is required for its validity which has limited its applicability to static graphs and transductive regimes. We propose to use unfolding, which allows any existing static GNN to output a dynamic graph embedding with exchangeability properties. Using this, we extend the validity of conformal prediction to dynamic GNNs in both transductive and semi-inductive regimes. We provide a theoretical guarantee of valid conformal prediction in these cases and demonstrate the empirical validity, as well as the performance gains, of unfolded GNNs against standard GNN architectures on both simulated and real datasets.

A Simple and Powerful Framework for Stable Dynamic Network Embedding

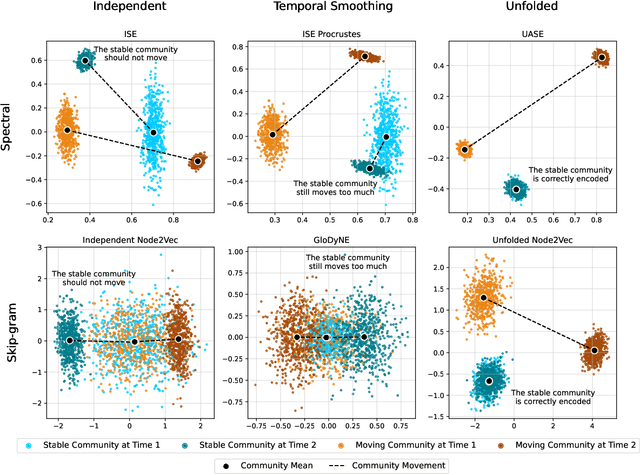
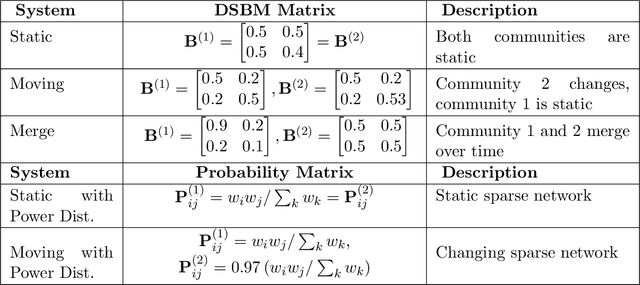
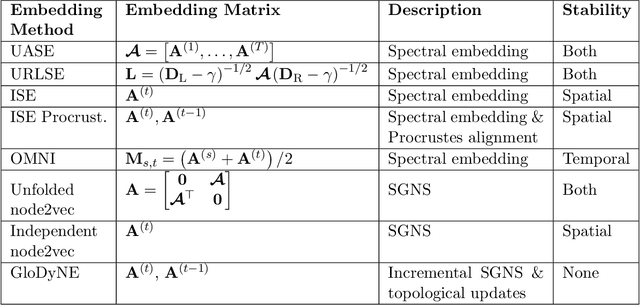
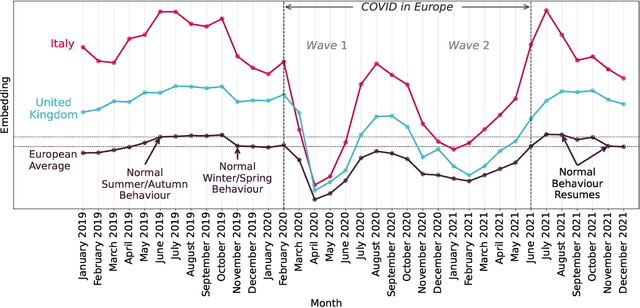
In this paper, we address the problem of dynamic network embedding, that is, representing the nodes of a dynamic network as evolving vectors within a low-dimensional space. While the field of static network embedding is wide and established, the field of dynamic network embedding is comparatively in its infancy. We propose that a wide class of established static network embedding methods can be used to produce interpretable and powerful dynamic network embeddings when they are applied to the dilated unfolded adjacency matrix. We provide a theoretical guarantee that, regardless of embedding dimension, these unfolded methods will produce stable embeddings, meaning that nodes with identical latent behaviour will be exchangeable, regardless of their position in time or space. We additionally define a hypothesis testing framework which can be used to evaluate the quality of a dynamic network embedding by testing for planted structure in simulated networks. Using this, we demonstrate that, even in trivial cases, unstable methods are often either conservative or encode incorrect structure. In contrast, we demonstrate that our suite of stable unfolded methods are not only more interpretable but also more powerful in comparison to their unstable counterparts.

Intensity Profile Projection: A Framework for Continuous-Time Representation Learning for Dynamic Networks

We present a new algorithmic framework, Intensity Profile Projection, for learning continuous-time representations of the nodes of a dynamic network, characterised by a node set and a collection of instantaneous interaction events which occur in continuous time. Our framework consists of three stages: estimating the intensity functions underlying the interactions between pairs of nodes, e.g. via kernel smoothing; learning a projection which minimises a notion of intensity reconstruction error; and inductively constructing evolving node representations via the learned projection. We show that our representations preserve the underlying structure of the network, and are temporally coherent, meaning that node representations can be meaningfully compared at different points in time. We develop estimation theory which elucidates the role of smoothing as a bias-variance trade-off, and shows how we can reduce smoothing as the signal-to-noise ratio increases on account of the algorithm `borrowing strength' across the network.

Spectral embedding and the latent geometry of multipartite networks

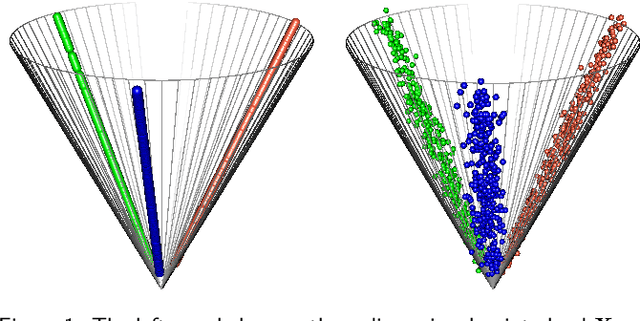
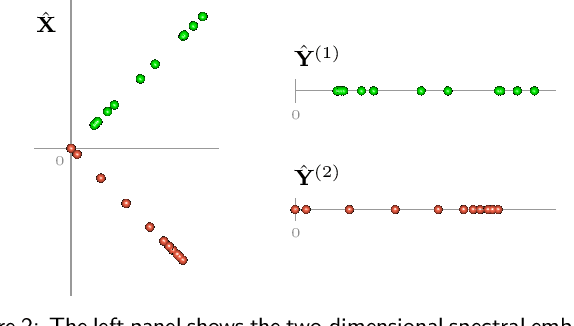
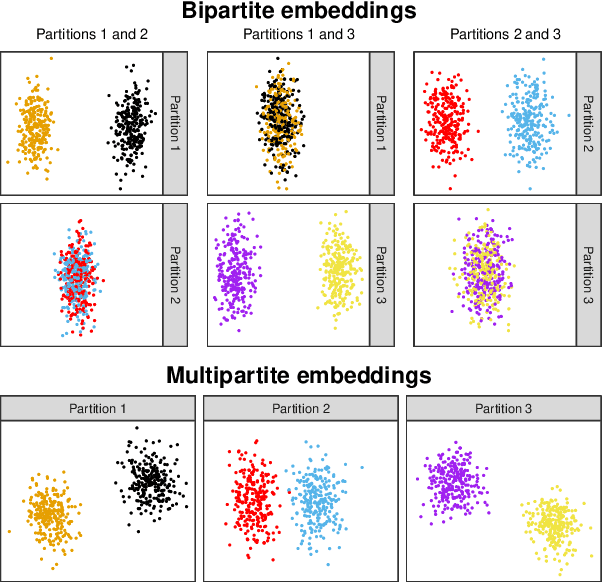
Spectral embedding finds vector representations of the nodes of a network, based on the eigenvectors of its adjacency or Laplacian matrix, and has found applications throughout the sciences. Many such networks are multipartite, meaning their nodes can be divided into partitions and nodes of the same partition are never connected. When the network is multipartite, this paper demonstrates that the node representations obtained via spectral embedding live near partition-specific low-dimensional subspaces of a higher-dimensional ambient space. For this reason we propose a follow-on step after spectral embedding, to recover node representations in their intrinsic rather than ambient dimension, proving uniform consistency under a low-rank, inhomogeneous random graph model. Our method naturally generalizes bipartite spectral embedding, in which node representations are obtained by singular value decomposition of the biadjacency or bi-Laplacian matrix.

Spectral embedding for dynamic networks with stability guarantees

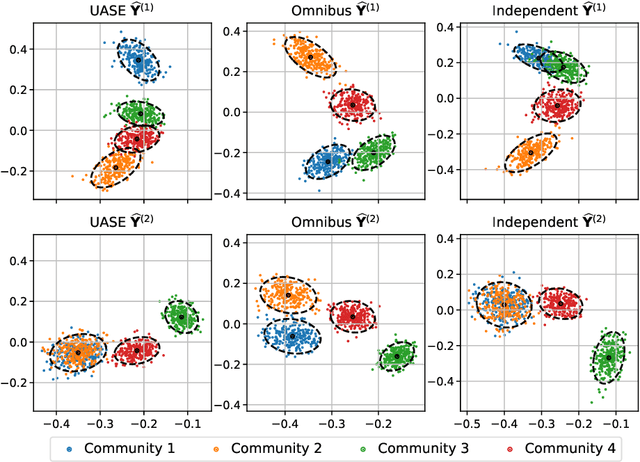
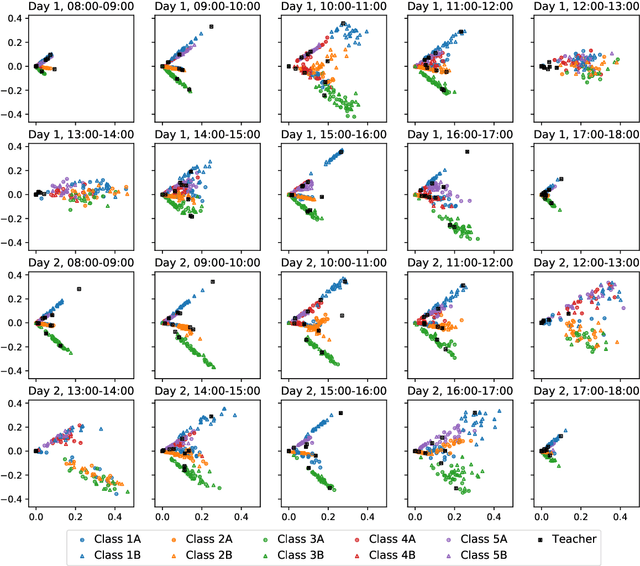
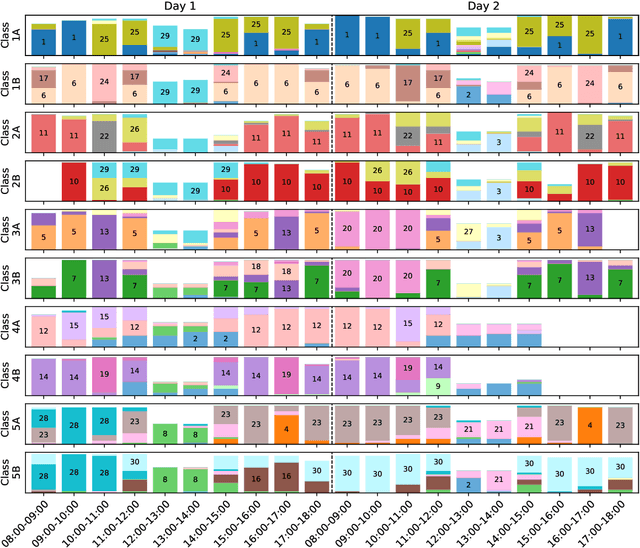
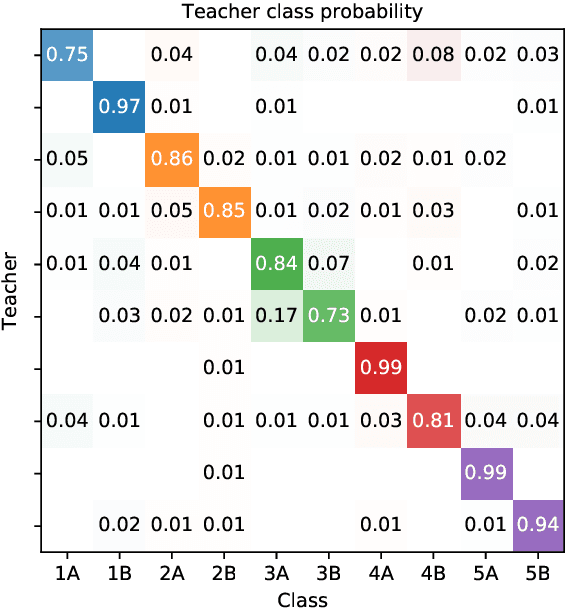
We consider the problem of embedding a dynamic network, to obtain time-evolving vector representations of each node, which can then be used to describe the changes in behaviour of a single node, one or more communities, or the entire graph. Given this open-ended remit, we wish to guarantee stability in the spatio-temporal positioning of the nodes: assigning the same position, up to noise, to nodes behaving similarly at a given time (cross-sectional stability) and a constant position, up to noise, to a single node behaving similarly across different times (longitudinal stability). These properties are defined formally within a generic dynamic latent position model. By showing how this model can be recast as a multilayer random dot product graph, we demonstrate that unfolded adjacency spectral embedding satisfies both stability conditions, allowing, for example, spatio-temporal clustering under the dynamic stochastic block model. We also show how alternative methods, such as omnibus, independent or time-averaged spectral embedding, lack one or the other form of stability.

Spectral clustering in the weighted stochastic block model

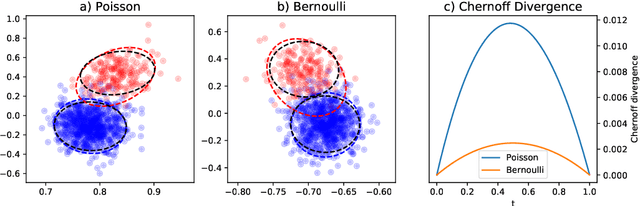
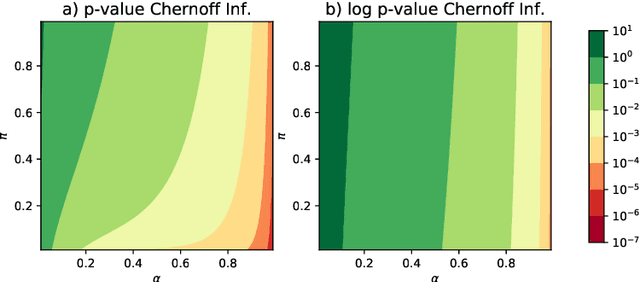
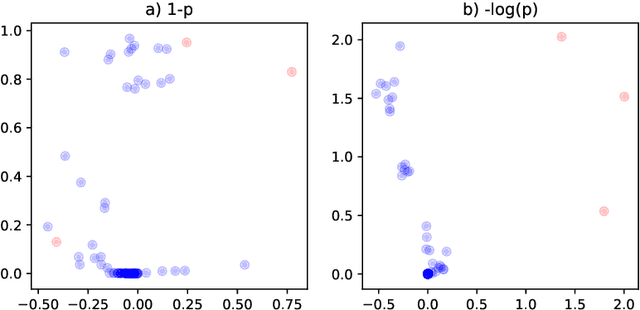
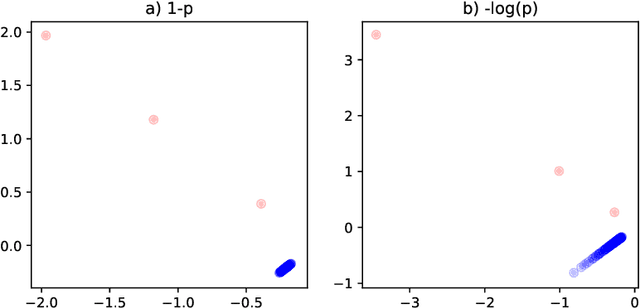
This paper is concerned with the statistical analysis of a real-valued symmetric data matrix. We assume a weighted stochastic block model: the matrix indices, taken to represent nodes, can be partitioned into communities so that all entries corresponding to a given community pair are replicates of the same random variable. Extending results previously known only for unweighted graphs, we provide a limit theorem showing that the point cloud obtained from spectrally embedding the data matrix follows a Gaussian mixture model where each community is represented with an elliptical component. We can therefore formally evaluate how well the communities separate under different data transformations, for example, whether it is productive to "take logs". We find that performance is invariant to affine transformation of the entries, but this expected and desirable feature hinges on adaptively selecting the eigenvectors according to eigenvalue magnitude and using Gaussian clustering. We present a network anomaly detection problem with cyber-security data where the matrix of log p-values, as opposed to p-values, has both theoretical and empirical advantages.