Valid Bootstraps for Networks with Applications to Network Visualisation

Quantifying uncertainty in networks is an important step in modelling relationships and interactions between entities. We consider the challenge of bootstrapping an inhomogeneous random graph when only a single observation of the network is made and the underlying data generating function is unknown. We utilise an exchangeable network test that can empirically validate bootstrap samples generated by any method, by testing if the observed and bootstrapped networks are statistically distinguishable. We find that existing methods fail this test. To address this, we propose a principled, novel, distribution-free network bootstrap using k-nearest neighbour smoothing, that can regularly pass this exchangeable network test in both synthetic and real-data scenarios. We demonstrate the utility of this work in combination with the popular data visualisation method t-SNE, where uncertainty estimates from bootstrapping are used to explain whether visible structures represent real statistically sound structures.

Valid Conformal Prediction for Dynamic GNNs

Graph neural networks (GNNs) are powerful black-box models which have shown impressive empirical performance. However, without any form of uncertainty quantification, it can be difficult to trust such models in high-risk scenarios. Conformal prediction aims to address this problem, however, an assumption of exchangeability is required for its validity which has limited its applicability to static graphs and transductive regimes. We propose to use unfolding, which allows any existing static GNN to output a dynamic graph embedding with exchangeability properties. Using this, we extend the validity of conformal prediction to dynamic GNNs in both transductive and semi-inductive regimes. We provide a theoretical guarantee of valid conformal prediction in these cases and demonstrate the empirical validity, as well as the performance gains, of unfolded GNNs against standard GNN architectures on both simulated and real datasets.

A Simple and Powerful Framework for Stable Dynamic Network Embedding

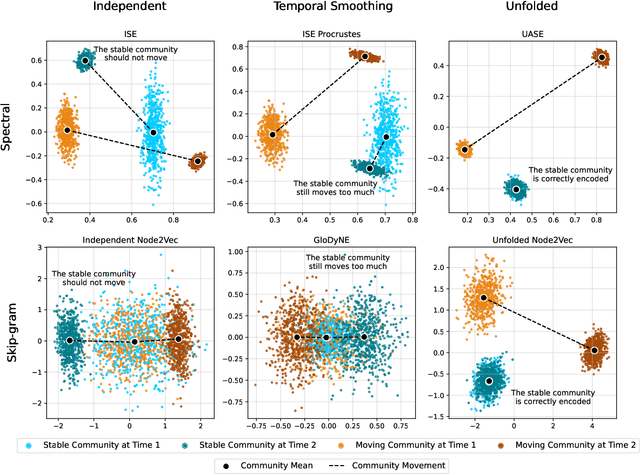
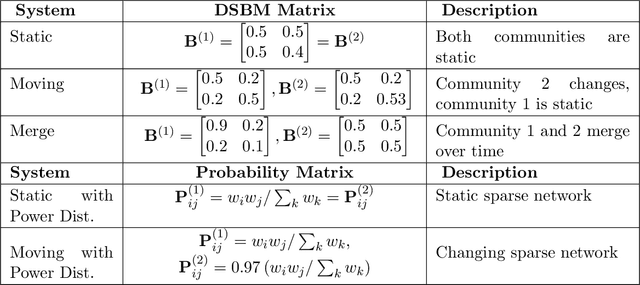
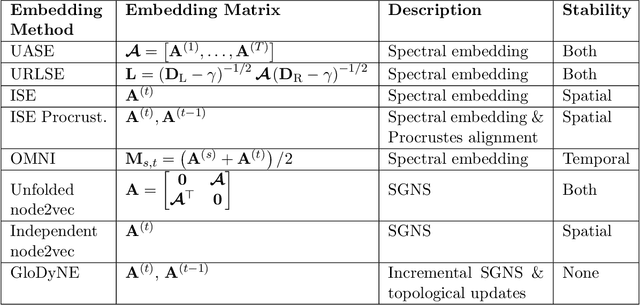
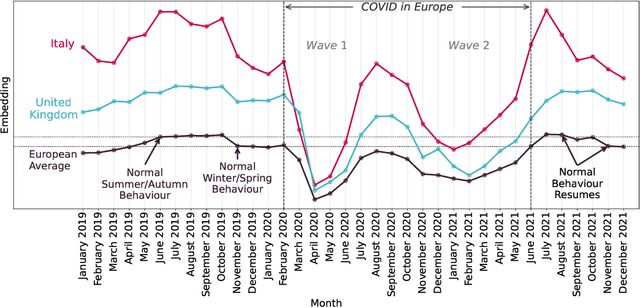
In this paper, we address the problem of dynamic network embedding, that is, representing the nodes of a dynamic network as evolving vectors within a low-dimensional space. While the field of static network embedding is wide and established, the field of dynamic network embedding is comparatively in its infancy. We propose that a wide class of established static network embedding methods can be used to produce interpretable and powerful dynamic network embeddings when they are applied to the dilated unfolded adjacency matrix. We provide a theoretical guarantee that, regardless of embedding dimension, these unfolded methods will produce stable embeddings, meaning that nodes with identical latent behaviour will be exchangeable, regardless of their position in time or space. We additionally define a hypothesis testing framework which can be used to evaluate the quality of a dynamic network embedding by testing for planted structure in simulated networks. Using this, we demonstrate that, even in trivial cases, unstable methods are often either conservative or encode incorrect structure. In contrast, we demonstrate that our suite of stable unfolded methods are not only more interpretable but also more powerful in comparison to their unstable counterparts.