Anna Bertiger
Spectral clustering in the weighted stochastic block model
Oct 12, 2019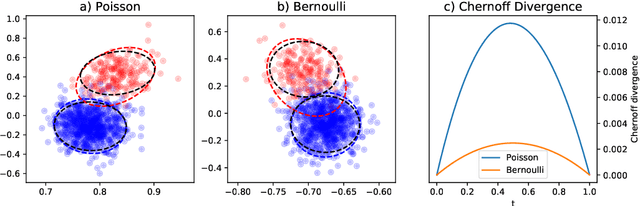
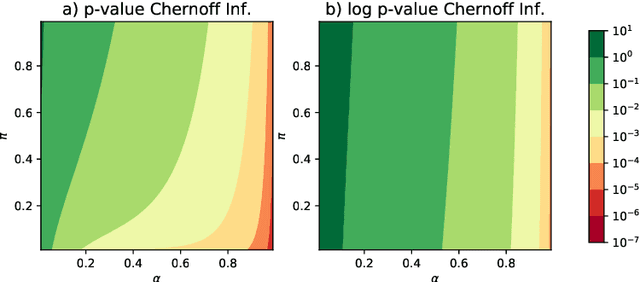
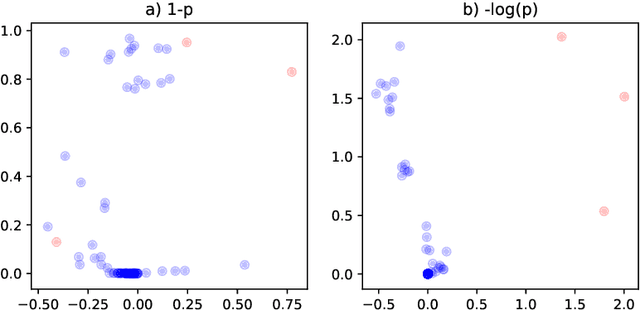
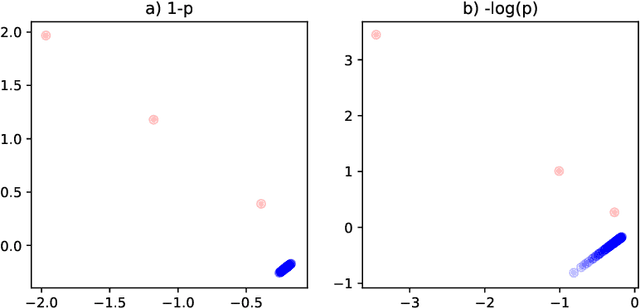
Abstract:This paper is concerned with the statistical analysis of a real-valued symmetric data matrix. We assume a weighted stochastic block model: the matrix indices, taken to represent nodes, can be partitioned into communities so that all entries corresponding to a given community pair are replicates of the same random variable. Extending results previously known only for unweighted graphs, we provide a limit theorem showing that the point cloud obtained from spectrally embedding the data matrix follows a Gaussian mixture model where each community is represented with an elliptical component. We can therefore formally evaluate how well the communities separate under different data transformations, for example, whether it is productive to "take logs". We find that performance is invariant to affine transformation of the entries, but this expected and desirable feature hinges on adaptively selecting the eigenvectors according to eigenvalue magnitude and using Gaussian clustering. We present a network anomaly detection problem with cyber-security data where the matrix of log p-values, as opposed to p-values, has both theoretical and empirical advantages.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge