How high is `high'? Rethinking the roles of dimensionality in topological data analysis and manifold learning

We present a generalised Hanson-Wright inequality and use it to establish new statistical insights into the geometry of data point-clouds. In the setting of a general random function model of data, we clarify the roles played by three notions of dimensionality: ambient intrinsic dimension $p_{\mathrm{int}}$, which measures total variability across orthogonal feature directions; correlation rank, which measures functional complexity across samples; and latent intrinsic dimension, which is the dimension of manifold structure hidden in data. Our analysis shows that in order for persistence diagrams to reveal latent homology and for manifold structure to emerge it is sufficient that $p_{\mathrm{int}}\gg \log n$, where $n$ is the sample size. Informed by these theoretical perspectives, we revisit the ground-breaking neuroscience discovery of toroidal structure in grid-cell activity made by Gardner et al. (Nature, 2022): our findings reveal, for the first time, evidence that this structure is in fact isometric to physical space, meaning that grid cell activity conveys a geometrically faithful representation of the real world.

GraphEval: A Knowledge-Graph Based LLM Hallucination Evaluation Framework

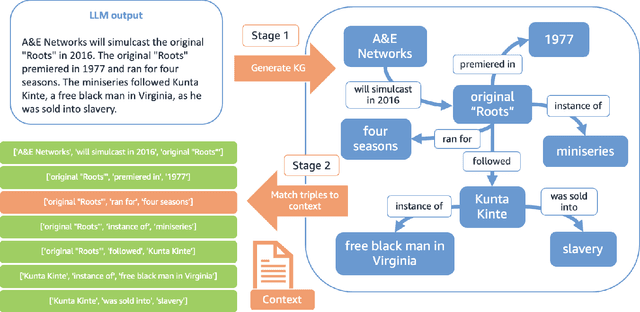
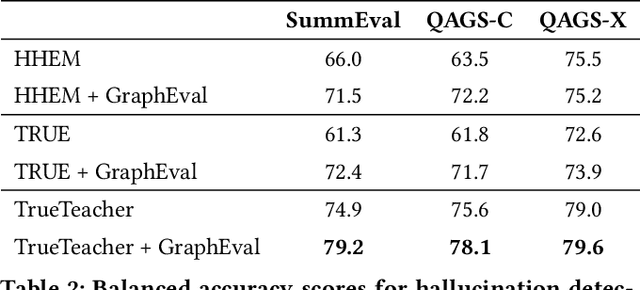
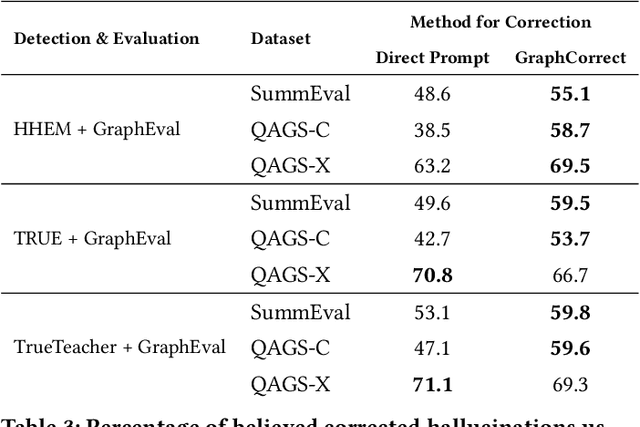
Methods to evaluate Large Language Model (LLM) responses and detect inconsistencies, also known as hallucinations, with respect to the provided knowledge, are becoming increasingly important for LLM applications. Current metrics fall short in their ability to provide explainable decisions, systematically check all pieces of information in the response, and are often too computationally expensive to be used in practice. We present GraphEval: a hallucination evaluation framework based on representing information in Knowledge Graph (KG) structures. Our method identifies the specific triples in the KG that are prone to hallucinations and hence provides more insight into where in the response a hallucination has occurred, if at all, than previous methods. Furthermore, using our approach in conjunction with state-of-the-art natural language inference (NLI) models leads to an improvement in balanced accuracy on various hallucination benchmarks, compared to using the raw NLI models. Lastly, we explore the use of GraphEval for hallucination correction by leveraging the structure of the KG, a method we name GraphCorrect, and demonstrate that the majority of hallucinations can indeed be rectified.

Implications of sparsity and high triangle density for graph representation learning

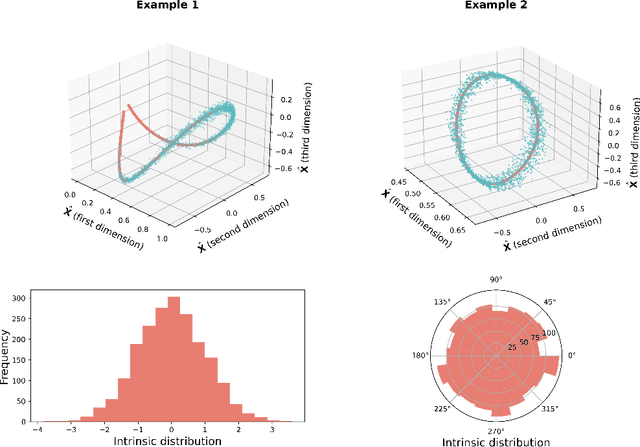
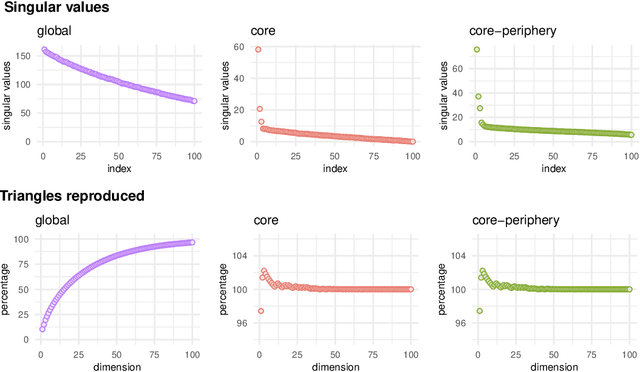
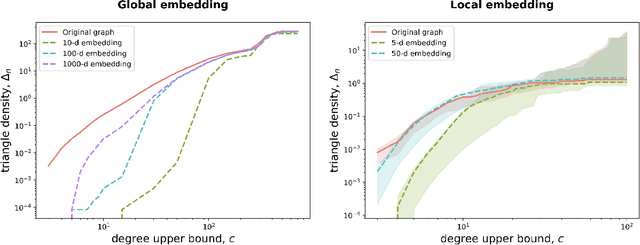
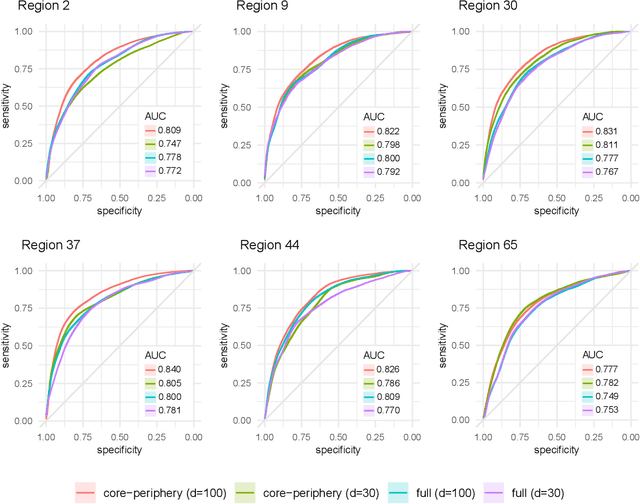
Recent work has shown that sparse graphs containing many triangles cannot be reproduced using a finite-dimensional representation of the nodes, in which link probabilities are inner products. Here, we show that such graphs can be reproduced using an infinite-dimensional inner product model, where the node representations lie on a low-dimensional manifold. Recovering a global representation of the manifold is impossible in a sparse regime. However, we can zoom in on local neighbourhoods, where a lower-dimensional representation is possible. As our constructions allow the points to be uniformly distributed on the manifold, we find evidence against the common perception that triangles imply community structure.