GraphEval: A Knowledge-Graph Based LLM Hallucination Evaluation Framework

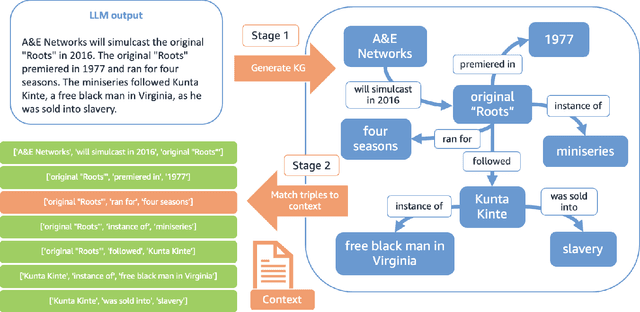
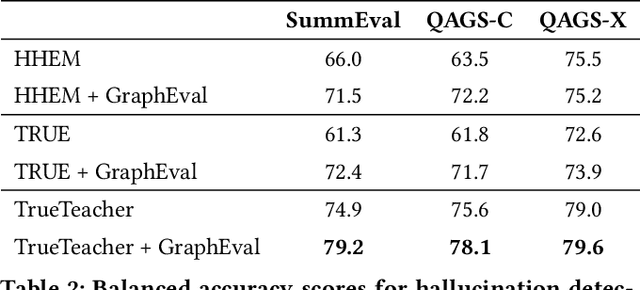
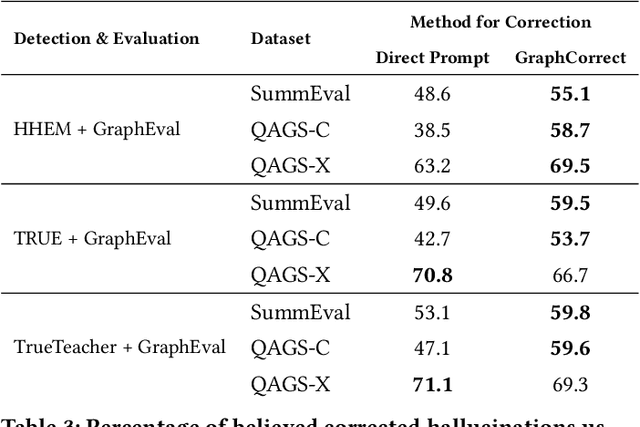
Methods to evaluate Large Language Model (LLM) responses and detect inconsistencies, also known as hallucinations, with respect to the provided knowledge, are becoming increasingly important for LLM applications. Current metrics fall short in their ability to provide explainable decisions, systematically check all pieces of information in the response, and are often too computationally expensive to be used in practice. We present GraphEval: a hallucination evaluation framework based on representing information in Knowledge Graph (KG) structures. Our method identifies the specific triples in the KG that are prone to hallucinations and hence provides more insight into where in the response a hallucination has occurred, if at all, than previous methods. Furthermore, using our approach in conjunction with state-of-the-art natural language inference (NLI) models leads to an improvement in balanced accuracy on various hallucination benchmarks, compared to using the raw NLI models. Lastly, we explore the use of GraphEval for hallucination correction by leveraging the structure of the KG, a method we name GraphCorrect, and demonstrate that the majority of hallucinations can indeed be rectified.

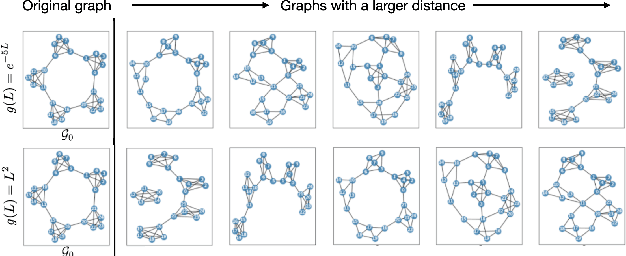
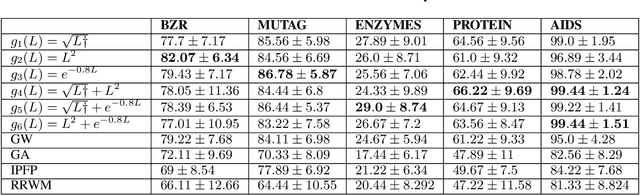
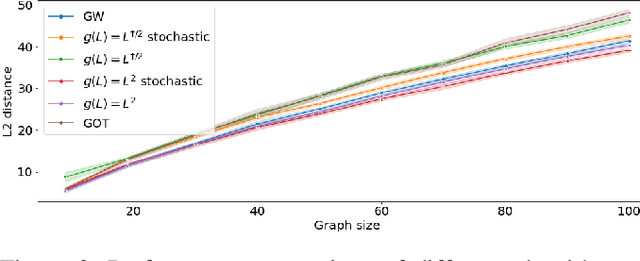
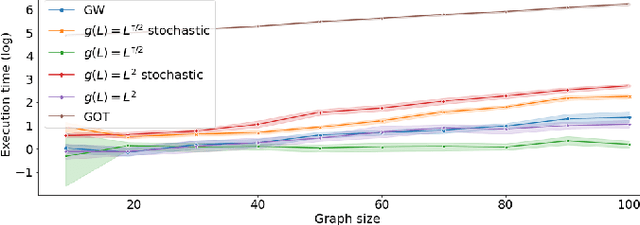
FGOT: Graph Distances based on Filters and Optimal Transport

Graph comparison deals with identifying similarities and dissimilarities between graphs. A major obstacle is the unknown alignment of graphs, as well as the lack of accurate and inexpensive comparison metrics. In this work we introduce the filter graph distance. It is an optimal transport based distance which drives graph comparison through the probability distribution of filtered graph signals. This creates a highly flexible distance, capable of prioritising different spectral information in observed graphs, offering a wide range of choices for a comparison metric. We tackle the problem of graph alignment by computing graph permutations that minimise our new filter distances, which implicitly solves the graph comparison problem. We then propose a new approximate cost function that circumvents many computational difficulties inherent to graph comparison and permits the exploitation of fast algorithms such as mirror gradient descent, without grossly sacrificing the performance. We finally propose a novel algorithm derived from a stochastic version of mirror gradient descent, which accommodates the non-convexity of the alignment problem, offering a good trade-off between performance accuracy and speed. The experiments on graph alignment and classification show that the flexibility gained through filter graph distances can have a significant impact on performance, while the difference in speed offered by the approximation cost makes the framework applicable in practical settings.

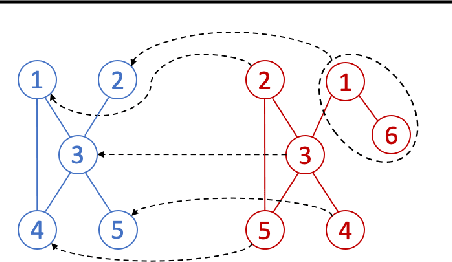
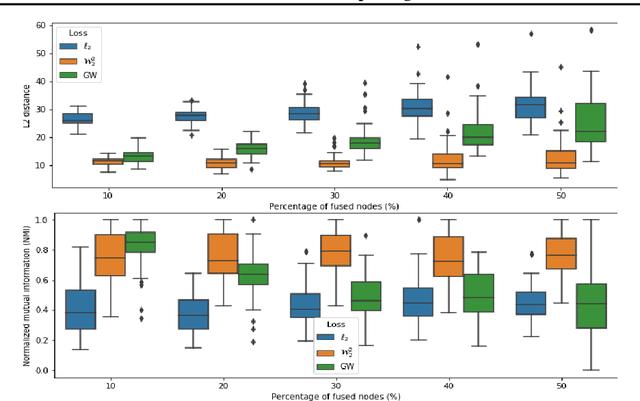
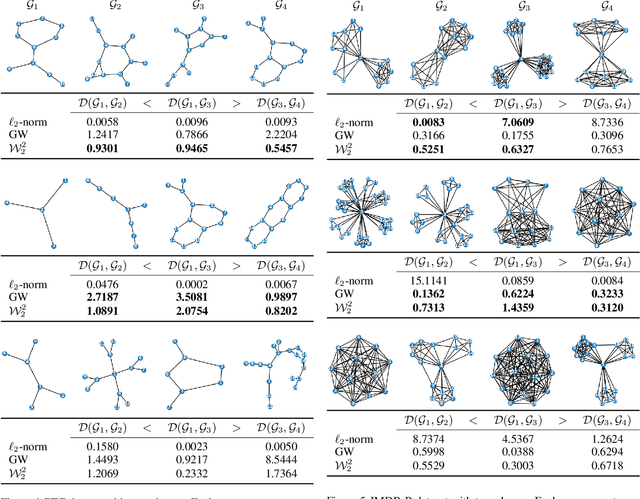
Wasserstein-based Graph Alignment

We propose a novel method for comparing non-aligned graphs of different sizes, based on the Wasserstein distance between graph signal distributions induced by the respective graph Laplacian matrices. Specifically, we cast a new formulation for the one-to-many graph alignment problem, which aims at matching a node in the smaller graph with one or more nodes in the larger graph. By integrating optimal transport in our graph comparison framework, we generate both a structurally-meaningful graph distance, and a signal transportation plan that models the structure of graph data. The resulting alignment problem is solved with stochastic gradient descent, where we use a novel Dykstra operator to ensure that the solution is a one-to-many (soft) assignment matrix. We demonstrate the performance of our novel framework on graph alignment and graph classification, and we show that our method leads to significant improvements with respect to the state-of-the-art algorithms for each of these tasks.

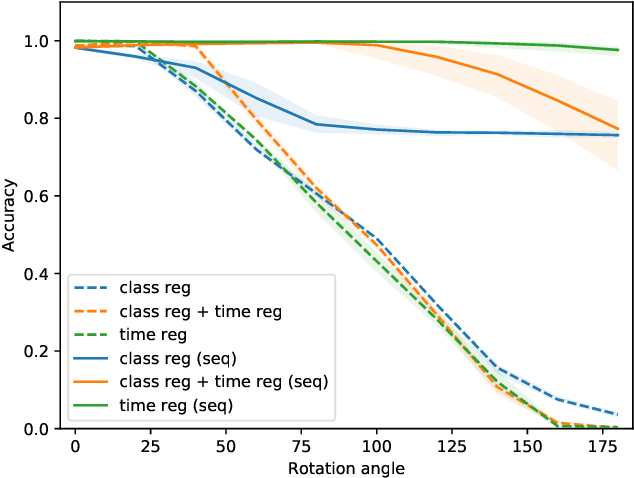
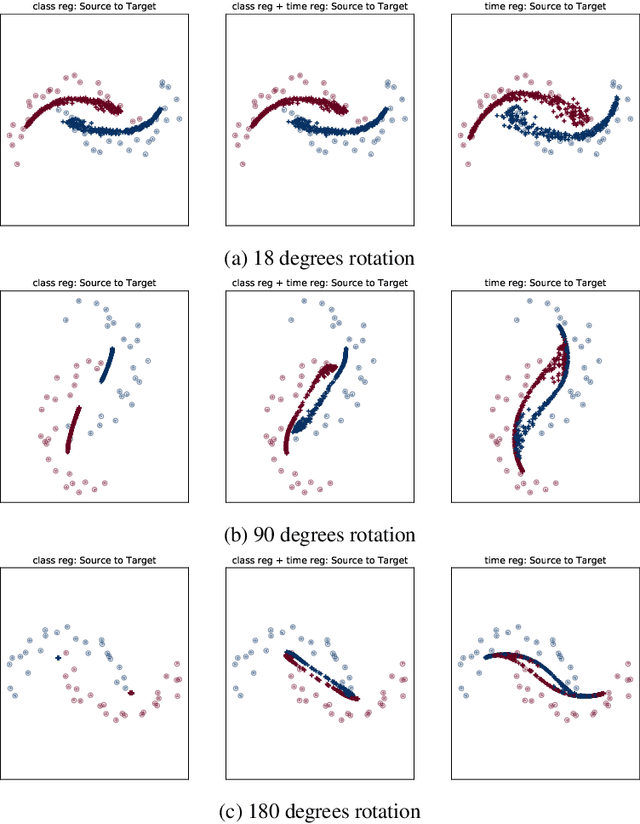
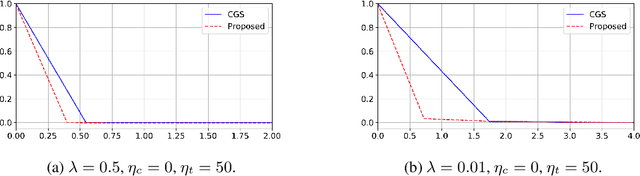
CDOT: Continuous Domain Adaptation using Optimal Transport

In this work, we address the scenario in which the target domain is continually, albeit slowly, evolving, and in which, at different time frames, we are given a batch of test data to classify. We exploit the geometry-awareness that optimal transport offers for the resolution of continuous domain adaptation problems. We propose a regularized optimal transport model that takes into account the transportation cost, the entropy of the probabilistic coupling, the labels of the source domain, and the similarity between successive target domains. The resulting optimization problem is efficiently solved with a forward-backward splitting algorithm based on Bregman distances. Experiments show that the proposed approach leads to a significant improvement in terms of speed and performance with respect to the state of the art.

GOT: An Optimal Transport framework for Graph comparison

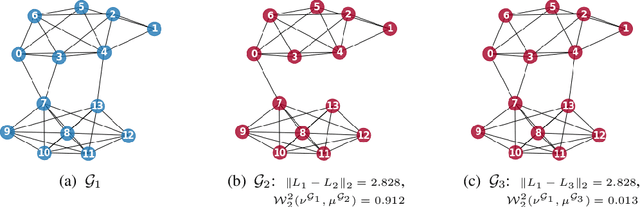
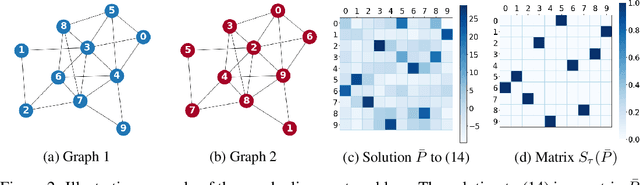
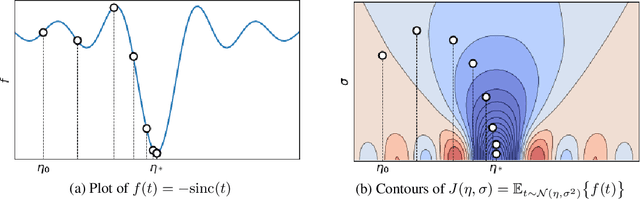
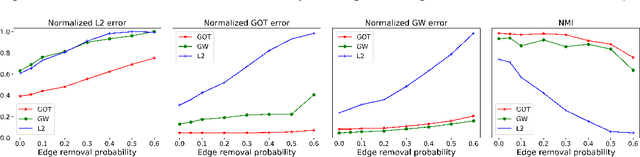
We present a novel framework based on optimal transport for the challenging problem of comparing graphs. Specifically, we exploit the probabilistic distribution of smooth graph signals defined with respect to the graph topology. This allows us to derive an explicit expression of the Wasserstein distance between graph signal distributions in terms of the graph Laplacian matrices. This leads to a structurally meaningful measure for comparing graphs, which is able to take into account the global structure of graphs, while most other measures merely observe local changes independently. Our measure is then used for formulating a new graph alignment problem, whose objective is to estimate the permutation that minimizes the distance between two graphs. We further propose an efficient stochastic algorithm based on Bayesian exploration to accommodate for the non-convexity of the graph alignment problem. We finally demonstrate the performance of our novel framework on different tasks like graph alignment, graph classification and graph signal prediction, and we show that our method leads to significant improvement with respect to the-state-of-art algorithms.

Graph heat mixture model learning

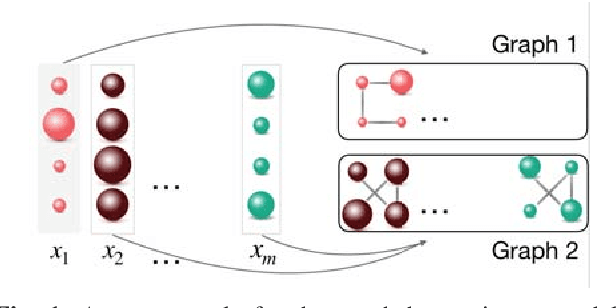
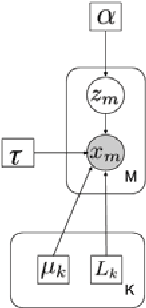
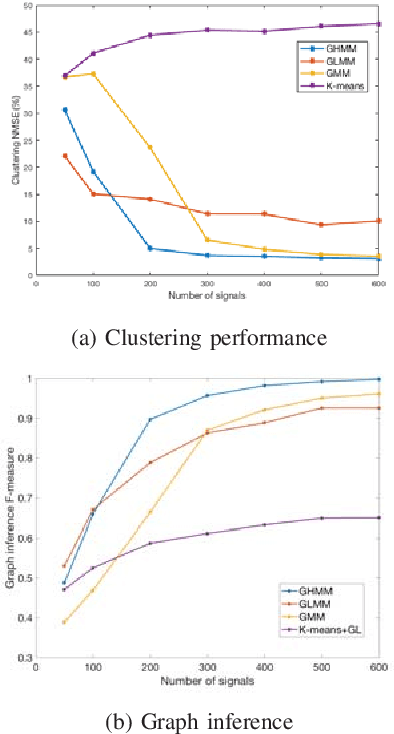
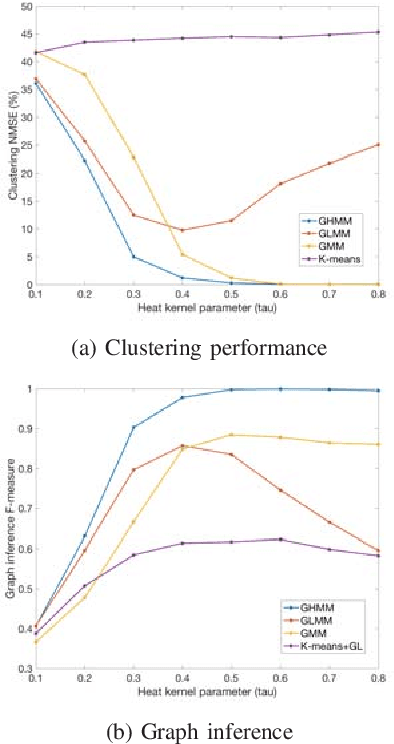
Graph inference methods have recently attracted a great interest from the scientific community, due to the large value they bring in data interpretation and analysis. However, most of the available state-of-the-art methods focus on scenarios where all available data can be explained through the same graph, or groups corresponding to each graph are known a priori. In this paper, we argue that this is not always realistic and we introduce a generative model for mixed signals following a heat diffusion process on multiple graphs. We propose an expectation-maximisation algorithm that can successfully separate signals into corresponding groups, and infer multiple graphs that govern their behaviour. We demonstrate the benefits of our method on both synthetic and real data.

Graph Laplacian mixture model

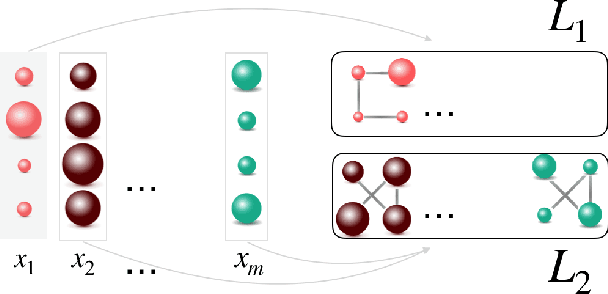
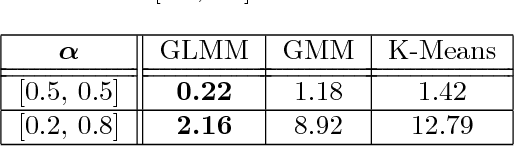
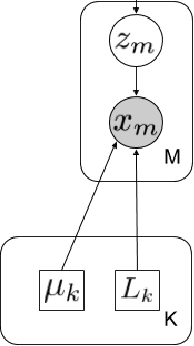
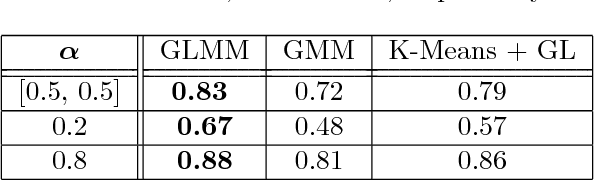
Graph learning methods have recently been receiving increasing interest as means to infer structure in datasets. Most of the recent approaches focus on different relationships between a graph and data sample distributions, mostly in settings where all available relate to the same graph. This is, however, not always the case, as data is often available in mixed form, yielding the need for methods that are able to cope with mixture data and learn multiple graphs. We propose a novel generative model that explains a collection of distinct data naturally living on different graphs. We assume the mapping of data to graphs is not known and investigate the problem of jointly clustering a set of data and learning a graph for each of the clusters. Experiments in both synthetic and real-world datasets demonstrate promising performance both in terms of data clustering, as well as multiple graph inference from mixture data.

Graph learning under sparsity priors

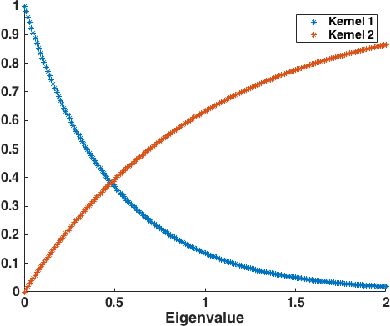
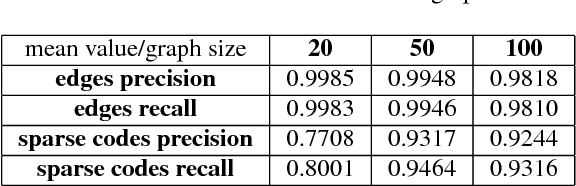
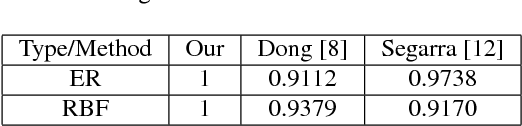
Graph signals offer a very generic and natural representation for data that lives on networks or irregular structures. The actual data structure is however often unknown a priori but can sometimes be estimated from the knowledge of the application domain. If this is not possible, the data structure has to be inferred from the mere signal observations. This is exactly the problem that we address in this paper, under the assumption that the graph signals can be represented as a sparse linear combination of a few atoms of a structured graph dictionary. The dictionary is constructed on polynomials of the graph Laplacian, which can sparsely represent a general class of graph signals composed of localized patterns on the graph. We formulate a graph learning problem, whose solution provides an ideal fit between the signal observations and the sparse graph signal model. As the problem is non-convex, we propose to solve it by alternating between a signal sparse coding and a graph update step. We provide experimental results that outline the good graph recovery performance of our method, which generally compares favourably to other recent network inference algorithms.