Mireille EL Gheche
GOT: An Optimal Transport framework for Graph comparison
Jun 05, 2019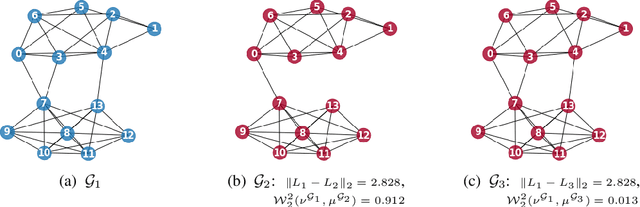
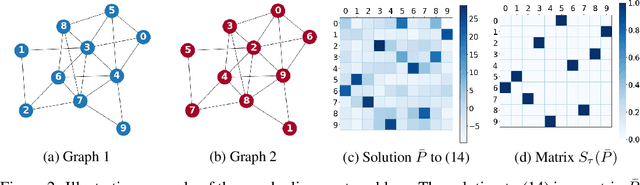
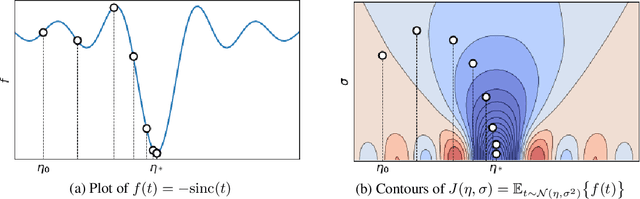
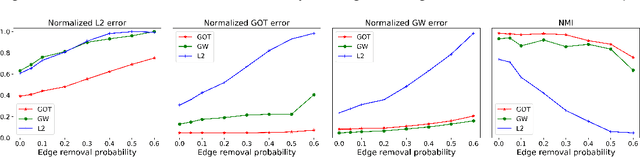
Abstract:We present a novel framework based on optimal transport for the challenging problem of comparing graphs. Specifically, we exploit the probabilistic distribution of smooth graph signals defined with respect to the graph topology. This allows us to derive an explicit expression of the Wasserstein distance between graph signal distributions in terms of the graph Laplacian matrices. This leads to a structurally meaningful measure for comparing graphs, which is able to take into account the global structure of graphs, while most other measures merely observe local changes independently. Our measure is then used for formulating a new graph alignment problem, whose objective is to estimate the permutation that minimizes the distance between two graphs. We further propose an efficient stochastic algorithm based on Bayesian exploration to accommodate for the non-convexity of the graph alignment problem. We finally demonstrate the performance of our novel framework on different tasks like graph alignment, graph classification and graph signal prediction, and we show that our method leads to significant improvement with respect to the-state-of-art algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge