Distributed Graph Learning with Smooth Data Priors

Graph learning is often a necessary step in processing or representing structured data, when the underlying graph is not given explicitly. Graph learning is generally performed centrally with a full knowledge of the graph signals, namely the data that lives on the graph nodes. However, there are settings where data cannot be collected easily or only with a non-negligible communication cost. In such cases, distributed processing appears as a natural solution, where the data stays mostly local and all processing is performed among neighbours nodes on the communication graph. We propose here a novel distributed graph learning algorithm, which permits to infer a graph from signal observations on the nodes under the assumption that the data is smooth on the target graph. We solve a distributed optimization problem with local projection constraints to infer a valid graph while limiting the communication costs. Our results show that the distributed approach has a lower communication cost than a centralised algorithm without compromising the accuracy in the inferred graph. It also scales better in communication costs with the increase of the network size, especially for sparse networks.

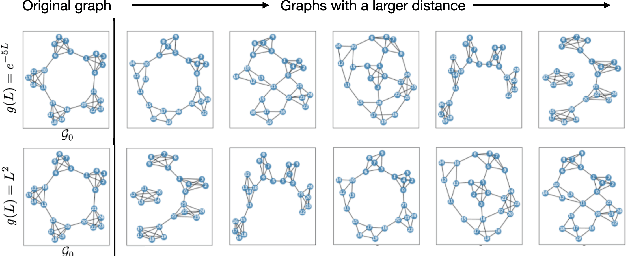
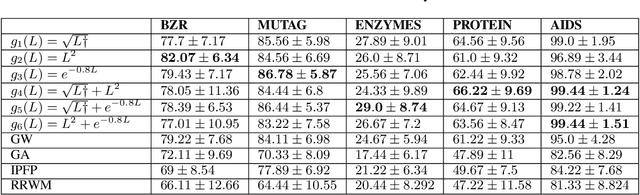
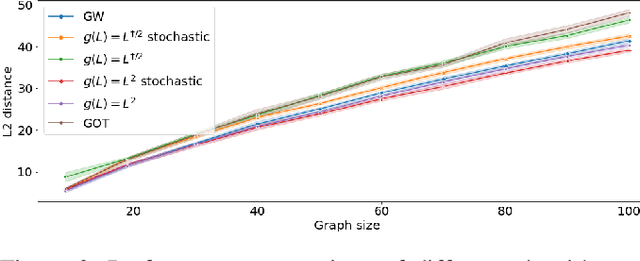
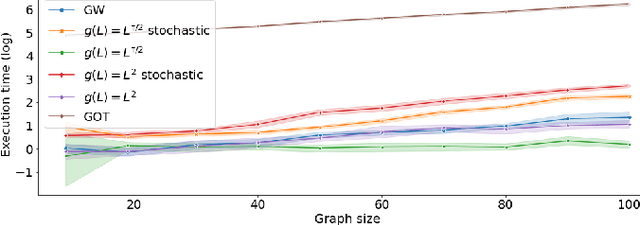
FGOT: Graph Distances based on Filters and Optimal Transport

Graph comparison deals with identifying similarities and dissimilarities between graphs. A major obstacle is the unknown alignment of graphs, as well as the lack of accurate and inexpensive comparison metrics. In this work we introduce the filter graph distance. It is an optimal transport based distance which drives graph comparison through the probability distribution of filtered graph signals. This creates a highly flexible distance, capable of prioritising different spectral information in observed graphs, offering a wide range of choices for a comparison metric. We tackle the problem of graph alignment by computing graph permutations that minimise our new filter distances, which implicitly solves the graph comparison problem. We then propose a new approximate cost function that circumvents many computational difficulties inherent to graph comparison and permits the exploitation of fast algorithms such as mirror gradient descent, without grossly sacrificing the performance. We finally propose a novel algorithm derived from a stochastic version of mirror gradient descent, which accommodates the non-convexity of the alignment problem, offering a good trade-off between performance accuracy and speed. The experiments on graph alignment and classification show that the flexibility gained through filter graph distances can have a significant impact on performance, while the difference in speed offered by the approximation cost makes the framework applicable in practical settings.

Multilayer Graph Clustering with Optimized Node Embedding

We are interested in multilayer graph clustering, which aims at dividing the graph nodes into categories or communities. To do so, we propose to learn a clustering-friendly embedding of the graph nodes by solving an optimization problem that involves a fidelity term to the layers of a given multilayer graph, and a regularization on the (single-layer) graph induced by the embedding. The fidelity term uses the contrastive loss to properly aggregate the observed layers into a representative embedding. The regularization pushes for a sparse and community-aware graph, and it is based on a measure of graph sparsification called "effective resistance", coupled with a penalization of the first few eigenvalues of the representative graph Laplacian matrix to favor the formation of communities. The proposed optimization problem is nonconvex but fully differentiable, and thus can be solved via the descent gradient method. Experiments show that our method leads to a significant improvement w.r.t. state-of-the-art multilayer graph clustering algorithms.

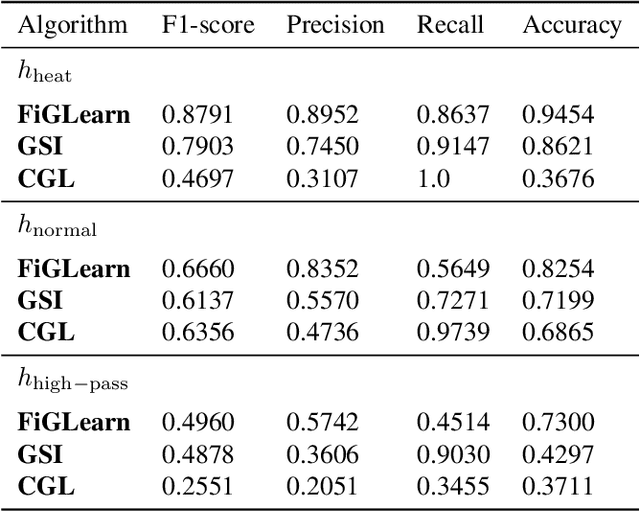
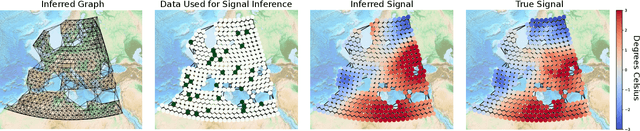
FiGLearn: Filter and Graph Learning using Optimal Transport

In many applications, a dataset can be considered as a set of observed signals that live on an unknown underlying graph structure. Some of these signals may be seen as white noise that has been filtered on the graph topology by a graph filter. Hence, the knowledge of the filter and the graph provides valuable information about the underlying data generation process and the complex interactions that arise in the dataset. We hence introduce a novel graph signal processing framework for jointly learning the graph and its generating filter from signal observations. We cast a new optimisation problem that minimises the Wasserstein distance between the distribution of the signal observations and the filtered signal distribution model. Our proposed method outperforms state-of-the-art graph learning frameworks on synthetic data. We then apply our method to a temperature anomaly dataset, and further show how this framework can be used to infer missing values if only very little information is available.

Multilayer Clustered Graph Learning

Multilayer graphs are appealing mathematical tools for modeling multiple types of relationship in the data. In this paper, we aim at analyzing multilayer graphs by properly combining the information provided by individual layers, while preserving the specific structure that allows us to eventually identify communities or clusters that are crucial in the analysis of graph data. To do so, we learn a clustered representative graph by solving an optimization problem that involves a data fidelity term to the observed layers, and a regularization pushing for a sparse and community-aware graph. We use the contrastive loss as a data fidelity term, in order to properly aggregate the observed layers into a representative graph. The regularization is based on a measure of graph sparsification called "effective resistance", coupled with a penalization of the first few eigenvalues of the representative graph Laplacian matrix to favor the formation of communities. The proposed optimization problem is nonconvex but fully differentiable, and thus can be solved via the projected gradient method. Experiments show that our method leads to a significant improvement w.r.t. state-of-the-art multilayer graph learning algorithms for solving clustering problems.

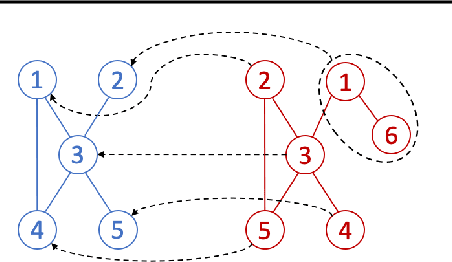
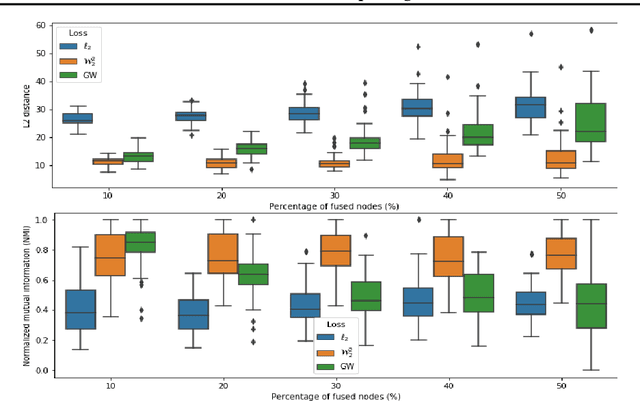
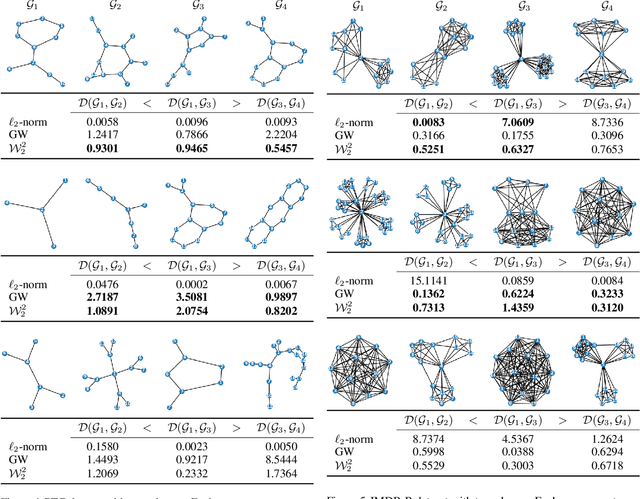
Wasserstein-based Graph Alignment

We propose a novel method for comparing non-aligned graphs of different sizes, based on the Wasserstein distance between graph signal distributions induced by the respective graph Laplacian matrices. Specifically, we cast a new formulation for the one-to-many graph alignment problem, which aims at matching a node in the smaller graph with one or more nodes in the larger graph. By integrating optimal transport in our graph comparison framework, we generate both a structurally-meaningful graph distance, and a signal transportation plan that models the structure of graph data. The resulting alignment problem is solved with stochastic gradient descent, where we use a novel Dykstra operator to ensure that the solution is a one-to-many (soft) assignment matrix. We demonstrate the performance of our novel framework on graph alignment and graph classification, and we show that our method leads to significant improvements with respect to the state-of-the-art algorithms for each of these tasks.

Joint Graph-based Depth Refinement and Normal Estimation

Depth estimation is an essential component in understanding the 3D geometry of a scene, with numerous applications in urban and indoor settings. These scenes are characterized by a prevalence of human made structures, which in most of the cases, are either inherently piece-wise planar, or can be approximated as such. In these settings, we devise a novel depth refinement framework that aims at recovering the underlying piece-wise planarity of the inverse depth map. We formulate this task as an optimization problem involving a data fidelity term that minimizes the distance to the input inverse depth map, as well as a regularization that enforces a piece-wise planar solution. As for the regularization term, we model the inverse depth map as a weighted graph between pixels. The proposed regularization is designed to estimate a plane automatically at each pixel, without any need for an a priori estimation of the scene planes, and at the same time it encourages similar pixels to be assigned to the same plane. The resulting optimization problem is efficiently solved with ADAM algorithm. Experiments show that our method leads to a significant improvement in depth refinement, both visually and numerically, with respect to state-of-the-art algorithms on Middlebury, KITTI and ETH3D multi-view stereo datasets.

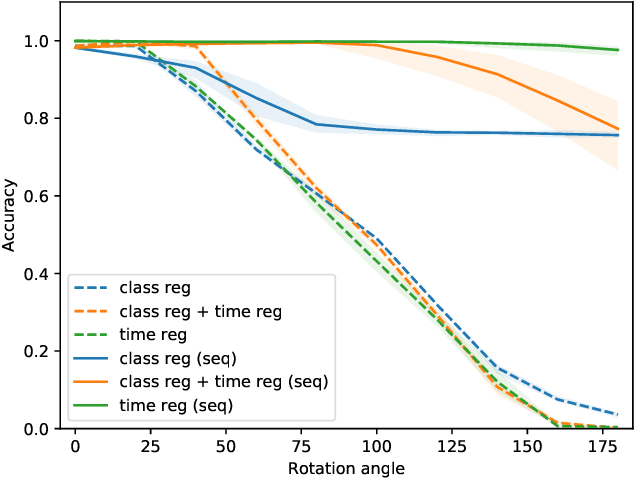
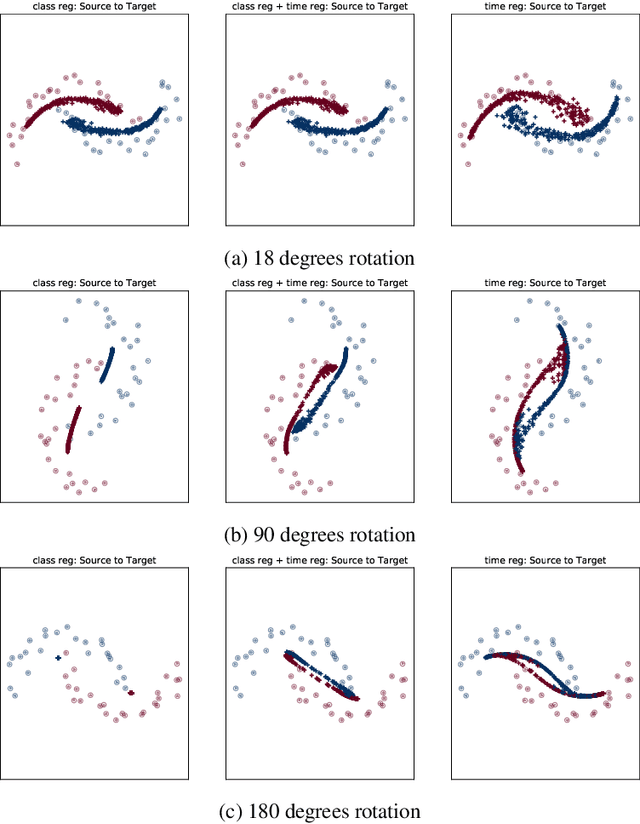
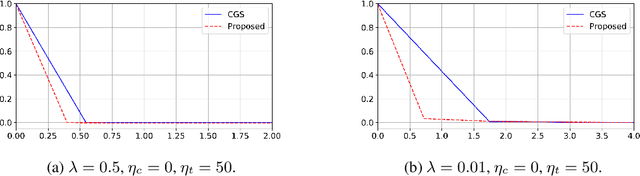
CDOT: Continuous Domain Adaptation using Optimal Transport

In this work, we address the scenario in which the target domain is continually, albeit slowly, evolving, and in which, at different time frames, we are given a batch of test data to classify. We exploit the geometry-awareness that optimal transport offers for the resolution of continuous domain adaptation problems. We propose a regularized optimal transport model that takes into account the transportation cost, the entropy of the probabilistic coupling, the labels of the source domain, and the similarity between successive target domains. The resulting optimization problem is efficiently solved with a forward-backward splitting algorithm based on Bregman distances. Experiments show that the proposed approach leads to a significant improvement in terms of speed and performance with respect to the state of the art.

Graph heat mixture model learning

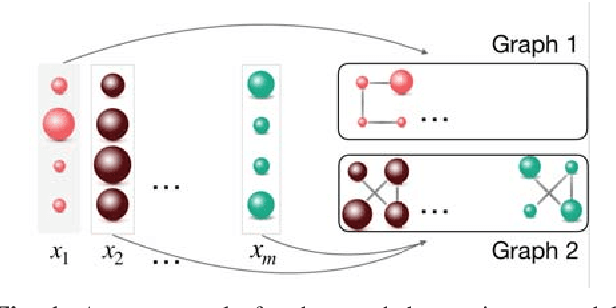
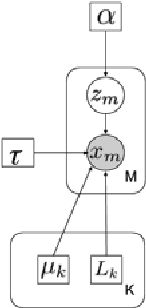
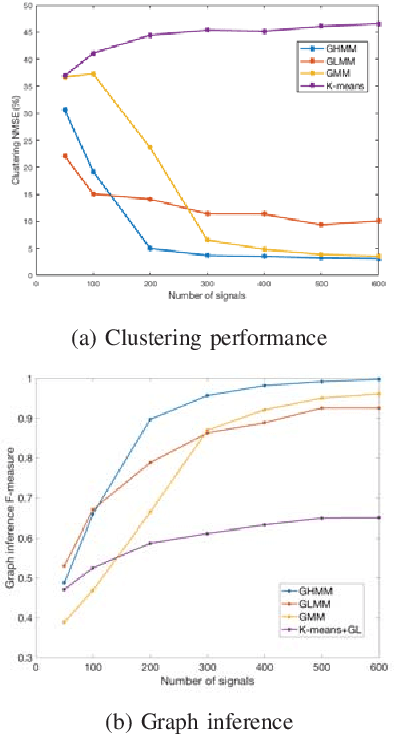
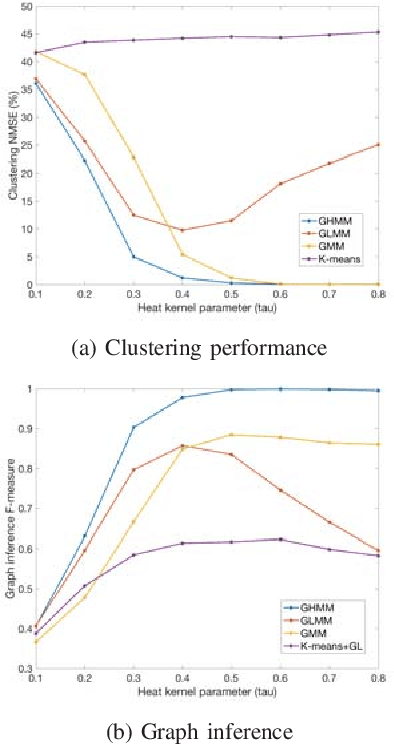
Graph inference methods have recently attracted a great interest from the scientific community, due to the large value they bring in data interpretation and analysis. However, most of the available state-of-the-art methods focus on scenarios where all available data can be explained through the same graph, or groups corresponding to each graph are known a priori. In this paper, we argue that this is not always realistic and we introduce a generative model for mixed signals following a heat diffusion process on multiple graphs. We propose an expectation-maximisation algorithm that can successfully separate signals into corresponding groups, and infer multiple graphs that govern their behaviour. We demonstrate the benefits of our method on both synthetic and real data.

Stochastic Gradient Descent for Spectral Embedding with Implicit Orthogonality Constraint

In this paper, we propose a scalable algorithm for spectral embedding. The latter is a standard tool for graph clustering. However, its computational bottleneck is the eigendecomposition of the graph Laplacian matrix, which prevents its application to large-scale graphs. Our contribution consists of reformulating spectral embedding so that it can be solved via stochastic optimization. The idea is to replace the orthogonality constraint with an orthogonalization matrix injected directly into the criterion. As the gradient can be computed through a Cholesky factorization, our reformulation allows us to develop an efficient algorithm based on mini-batch gradient descent. Experimental results, both on synthetic and real data, confirm the efficiency of the proposed method in term of execution speed with respect to similar existing techniques.