CDOT: Continuous Domain Adaptation using Optimal Transport
Paper and Code
Oct 03, 2019
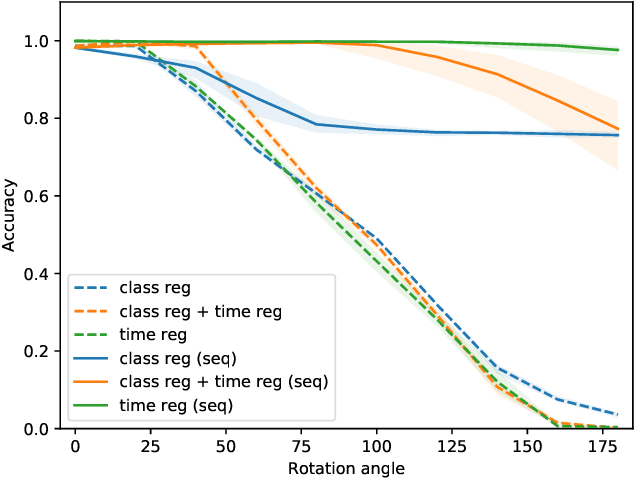
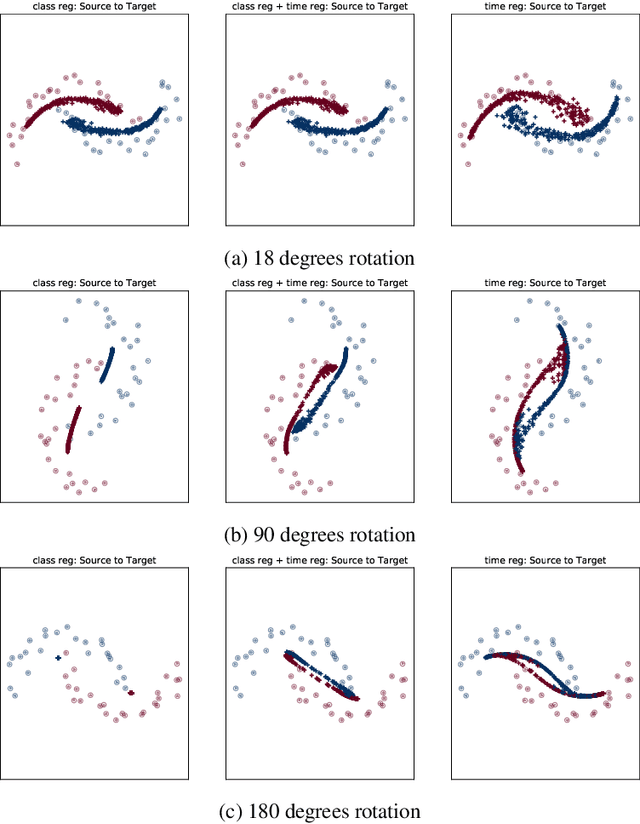
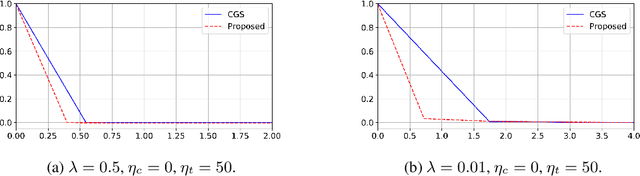
In this work, we address the scenario in which the target domain is continually, albeit slowly, evolving, and in which, at different time frames, we are given a batch of test data to classify. We exploit the geometry-awareness that optimal transport offers for the resolution of continuous domain adaptation problems. We propose a regularized optimal transport model that takes into account the transportation cost, the entropy of the probabilistic coupling, the labels of the source domain, and the similarity between successive target domains. The resulting optimization problem is efficiently solved with a forward-backward splitting algorithm based on Bregman distances. Experiments show that the proposed approach leads to a significant improvement in terms of speed and performance with respect to the state of the art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge