FlowPool: Pooling Graph Representations with Wasserstein Gradient Flows

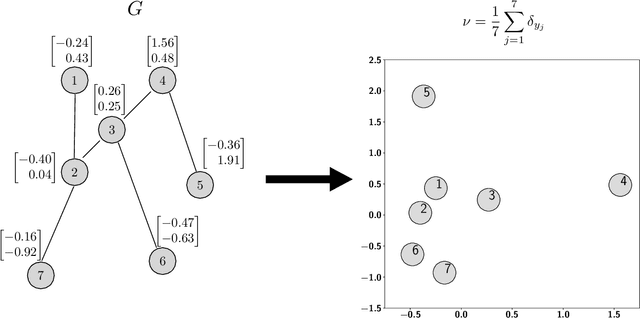
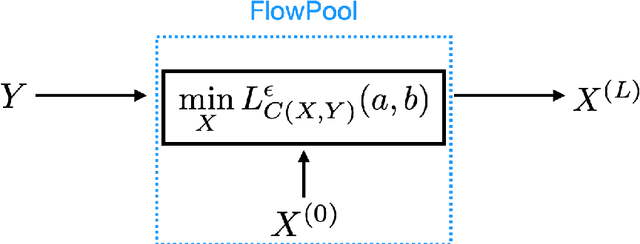
In several machine learning tasks for graph structured data, the graphs under consideration may be composed of a varying number of nodes. Therefore, it is necessary to design pooling methods that aggregate the graph representations of varying size to representations of fixed size which can be used in downstream tasks, such as graph classification. Existing graph pooling methods offer no guarantee with regards to the similarity of a graph representation and its pooled version. In this work we address this limitation by proposing FlowPool, a pooling method that optimally preserves the statistics of a graph representation to its pooled counterpart by minimizing their Wasserstein distance. This is achieved by performing a Wasserstein gradient flow with respect to the pooled graph representation. We propose a versatile implementation of our method which can take into account the geometry of the representation space through any ground cost. This implementation relies on the computation of the gradient of the Wasserstein distance with recently proposed implicit differentiation schemes. Our pooling method is amenable to automatic differentiation and can be integrated in end-to-end deep learning architectures. Further, FlowPool is invariant to permutations and can therefore be combined with permutation equivariant feature extraction layers in GNNs in order to obtain predictions that are independent of the ordering of the nodes. Experimental results demonstrate that our method leads to an increase in performance compared to existing pooling methods when evaluated in graph classification tasks.

node2coords: Graph Representation Learning with Wasserstein Barycenters

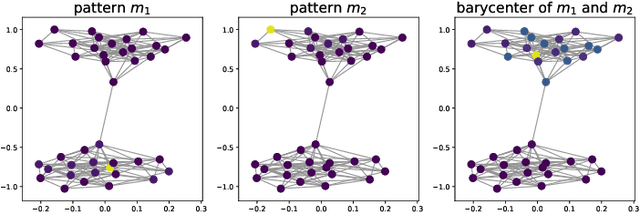
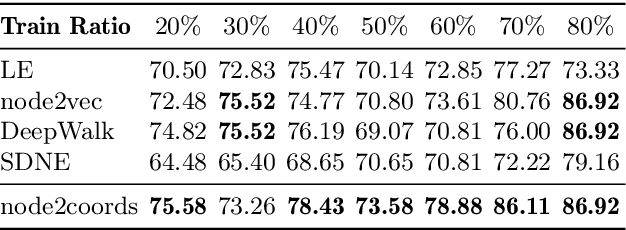
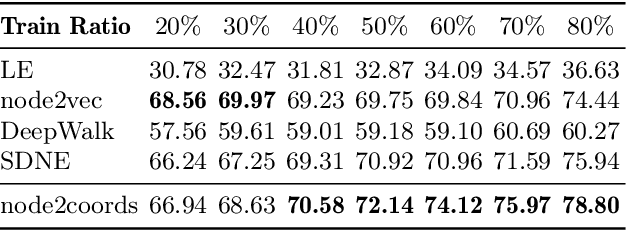
In order to perform network analysis tasks, representations that capture the most relevant information in the graph structure are needed. However, existing methods do not learn representations that can be interpreted in a straightforward way and that are robust to perturbations to the graph structure. In this work, we address these two limitations by proposing node2coords, a representation learning algorithm for graphs, which learns simultaneously a low-dimensional space and coordinates for the nodes in that space. The patterns that span the low dimensional space reveal the graph's most important structural information. The coordinates of the nodes reveal the proximity of their local structure to the graph structural patterns. In order to measure this proximity by taking into account the underlying graph, we propose to use Wasserstein distances. We introduce an autoencoder that employs a linear layer in the encoder and a novel Wasserstein barycentric layer at the decoder. Node connectivity descriptors, that capture the local structure of the nodes, are passed through the encoder to learn the small set of graph structural patterns. In the decoder, the node connectivity descriptors are reconstructed as Wasserstein barycenters of the graph structural patterns. The optimal weights for the barycenter representation of a node's connectivity descriptor correspond to the coordinates of that node in the low-dimensional space. Experimental results demonstrate that the representations learned with node2coords are interpretable, lead to node embeddings that are stable to perturbations of the graph structure and achieve competitive or superior results compared to state-of-the-art methods in node classification.

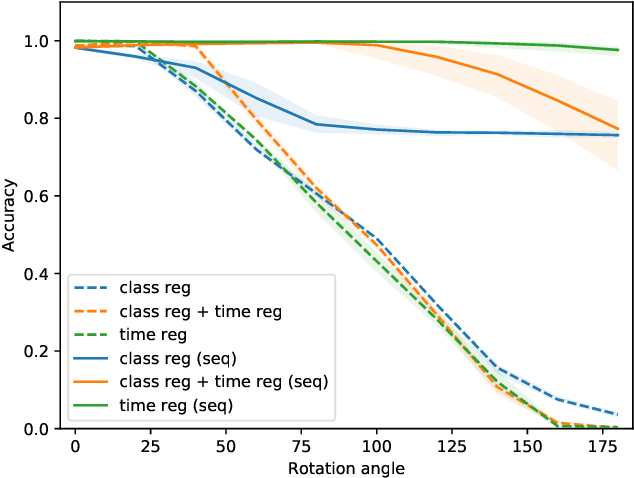
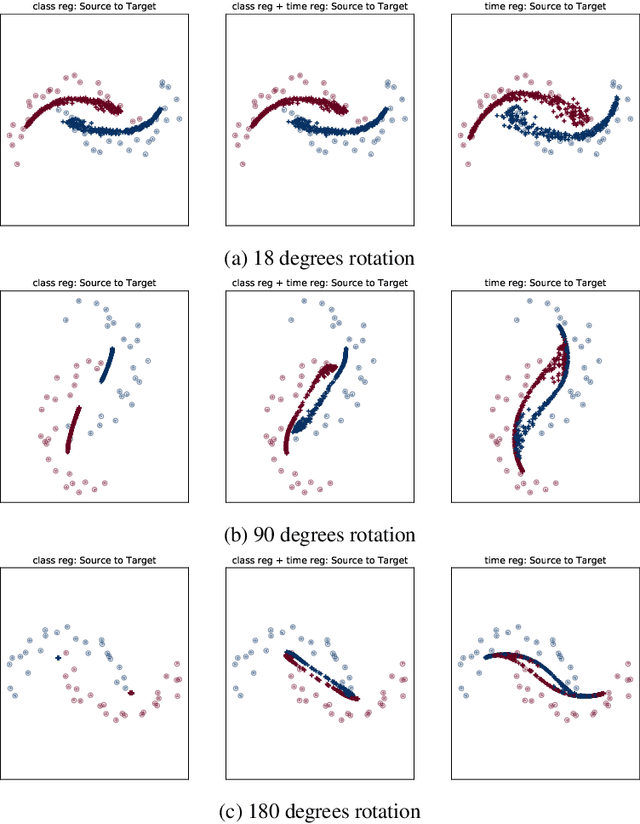
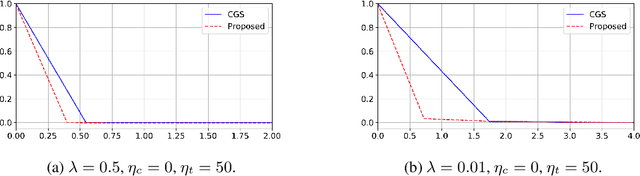
CDOT: Continuous Domain Adaptation using Optimal Transport

In this work, we address the scenario in which the target domain is continually, albeit slowly, evolving, and in which, at different time frames, we are given a batch of test data to classify. We exploit the geometry-awareness that optimal transport offers for the resolution of continuous domain adaptation problems. We propose a regularized optimal transport model that takes into account the transportation cost, the entropy of the probabilistic coupling, the labels of the source domain, and the similarity between successive target domains. The resulting optimization problem is efficiently solved with a forward-backward splitting algorithm based on Bregman distances. Experiments show that the proposed approach leads to a significant improvement in terms of speed and performance with respect to the state of the art.