Dorina Thanou
CM-UNet: A Self-Supervised Learning-Based Model for Coronary Artery Segmentation in X-Ray Angiography
Jul 22, 2025Abstract:Accurate segmentation of coronary arteries remains a significant challenge in clinical practice, hindering the ability to effectively diagnose and manage coronary artery disease. The lack of large, annotated datasets for model training exacerbates this issue, limiting the development of automated tools that could assist radiologists. To address this, we introduce CM-UNet, which leverages self-supervised pre-training on unannotated datasets and transfer learning on limited annotated data, enabling accurate disease detection while minimizing the need for extensive manual annotations. Fine-tuning CM-UNet with only 18 annotated images instead of 500 resulted in a 15.2% decrease in Dice score, compared to a 46.5% drop in baseline models without pre-training. This demonstrates that self-supervised learning can enhance segmentation performance and reduce dependence on large datasets. This is one of the first studies to highlight the importance of self-supervised learning in improving coronary artery segmentation from X-ray angiography, with potential implications for advancing diagnostic accuracy in clinical practice. By enhancing segmentation accuracy in X-ray angiography images, the proposed approach aims to improve clinical workflows, reduce radiologists' workload, and accelerate disease detection, ultimately contributing to better patient outcomes. The source code is publicly available at https://github.com/CamilleChallier/Contrastive-Masked-UNet.
Revisiting Automatic Data Curation for Vision Foundation Models in Digital Pathology
Mar 24, 2025Abstract:Vision foundation models (FMs) are accelerating the development of digital pathology algorithms and transforming biomedical research. These models learn, in a self-supervised manner, to represent histological features in highly heterogeneous tiles extracted from whole-slide images (WSIs) of real-world patient samples. The performance of these FMs is significantly influenced by the size, diversity, and balance of the pre-training data. However, data selection has been primarily guided by expert knowledge at the WSI level, focusing on factors such as disease classification and tissue types, while largely overlooking the granular details available at the tile level. In this paper, we investigate the potential of unsupervised automatic data curation at the tile-level, taking into account 350 million tiles. Specifically, we apply hierarchical clustering trees to pre-extracted tile embeddings, allowing us to sample balanced datasets uniformly across the embedding space of the pretrained FM. We further identify these datasets are subject to a trade-off between size and balance, potentially compromising the quality of representations learned by FMs, and propose tailored batch sampling strategies to mitigate this effect. We demonstrate the effectiveness of our method through improved performance on a diverse range of clinically relevant downstream tasks.
COSMOS: Continuous Simplicial Neural Networks
Mar 17, 2025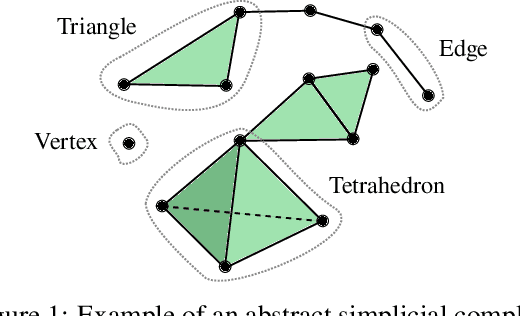
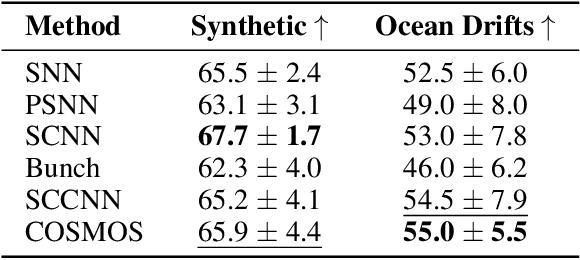


Abstract:Simplicial complexes provide a powerful framework for modeling high-order interactions in structured data, making them particularly suitable for applications such as trajectory prediction and mesh processing. However, existing simplicial neural networks (SNNs), whether convolutional or attention-based, rely primarily on discrete filtering techniques, which can be restrictive. In contrast, partial differential equations (PDEs) on simplicial complexes offer a principled approach to capture continuous dynamics in such structures. In this work, we introduce COntinuous SiMplicial neural netwOrkS (COSMOS), a novel SNN architecture derived from PDEs on simplicial complexes. We provide theoretical and experimental justifications of COSMOS's stability under simplicial perturbations. Furthermore, we investigate the over-smoothing phenomenon, a common issue in geometric deep learning, demonstrating that COSMOS offers better control over this effect than discrete SNNs. Our experiments on real-world datasets of ocean trajectory prediction and regression on partial deformable shapes demonstrate that COSMOS achieves competitive performance compared to state-of-the-art SNNs in complex and noisy environments.
DeFoG: Discrete Flow Matching for Graph Generation
Oct 05, 2024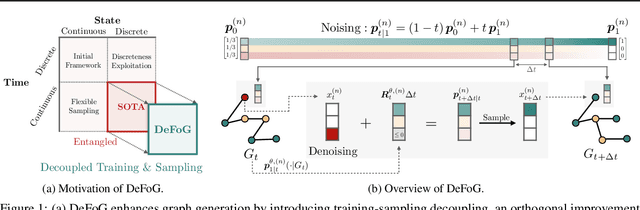



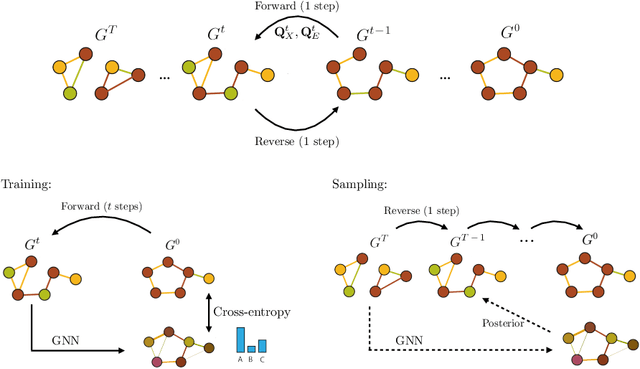
Abstract:Graph generation is fundamental in diverse scientific applications, due to its ability to reveal the underlying distribution of complex data, and eventually generate new, realistic data points. Despite the success of diffusion models in this domain, those face limitations in sampling efficiency and flexibility, stemming from the tight coupling between the training and sampling stages. To address this, we propose DeFoG, a novel framework using discrete flow matching for graph generation. DeFoG employs a flow-based approach that features an efficient linear interpolation noising process and a flexible denoising process based on a continuous-time Markov chain formulation. We leverage an expressive graph transformer and ensure desirable node permutation properties to respect graph symmetry. Crucially, our framework enables a disentangled design of the training and sampling stages, enabling more effective and efficient optimization of model performance. We navigate this design space by introducing several algorithmic improvements that boost the model performance, consistently surpassing existing diffusion models. We also theoretically demonstrate that, for general discrete data, discrete flow models can faithfully replicate the ground truth distribution - a result that naturally extends to graph data and reinforces DeFoG's foundations. Extensive experiments show that DeFoG achieves state-of-the-art results on synthetic and molecular datasets, improving both training and sampling efficiency over diffusion models, and excels in conditional generation on a digital pathology dataset.
Generative Modelling of Structurally Constrained Graphs
Jun 25, 2024


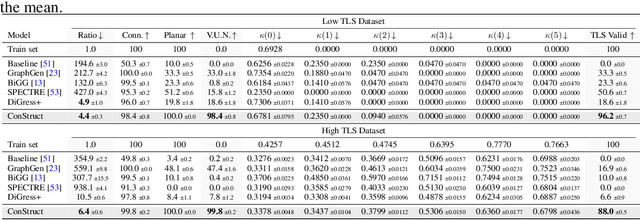
Abstract:Graph diffusion models have emerged as state-of-the-art techniques in graph generation, yet integrating domain knowledge into these models remains challenging. Domain knowledge is particularly important in real-world scenarios, where invalid generated graphs hinder deployment in practical applications. Unconstrained and conditioned graph generative models fail to guarantee such domain-specific structural properties. We present ConStruct, a novel framework that allows for hard-constraining graph diffusion models to incorporate specific properties, such as planarity or acyclicity. Our approach ensures that the sampled graphs remain within the domain of graphs that verify the specified property throughout the entire trajectory in both the forward and reverse processes. This is achieved by introducing a specific edge-absorbing noise model and a new projector operator. ConStruct demonstrates versatility across several structural and edge-deletion invariant constraints and achieves state-of-the-art performance for both synthetic benchmarks and attributed real-world datasets. For example, by leveraging planarity in digital pathology graph datasets, the proposed method outperforms existing baselines and enhances generated data validity by up to 71.1 percentage points.
Tertiary Lymphoid Structures Generation through Graph-based Diffusion
Oct 10, 2023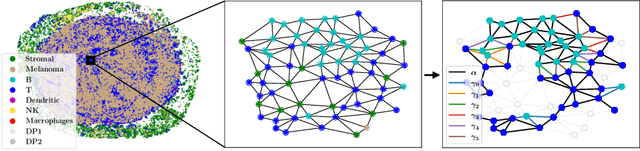


Abstract:Graph-based representation approaches have been proven to be successful in the analysis of biomedical data, due to their capability of capturing intricate dependencies between biological entities, such as the spatial organization of different cell types in a tumor tissue. However, to further enhance our understanding of the underlying governing biological mechanisms, it is important to accurately capture the actual distributions of such complex data. Graph-based deep generative models are specifically tailored to accomplish that. In this work, we leverage state-of-the-art graph-based diffusion models to generate biologically meaningful cell-graphs. In particular, we show that the adopted graph diffusion model is able to accurately learn the distribution of cells in terms of their tertiary lymphoid structures (TLS) content, a well-established biomarker for evaluating the cancer progression in oncology research. Additionally, we further illustrate the utility of the learned generative models for data augmentation in a TLS classification task. To the best of our knowledge, this is the first work that leverages the power of graph diffusion models in generating meaningful biological cell structures.
Reconstruction of Time-varying Graph Signals via Sobolev Smoothness
Jul 13, 2022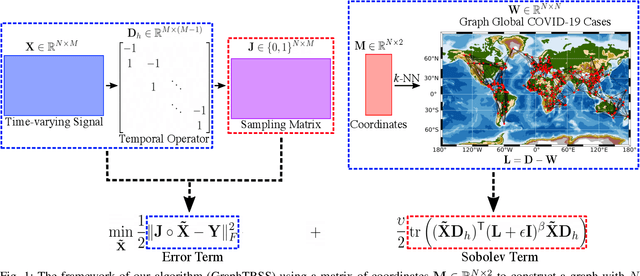
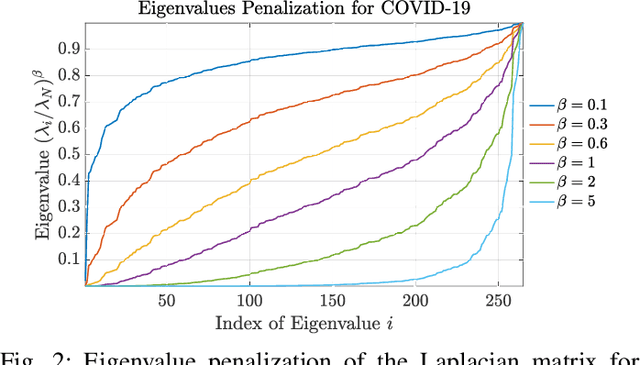
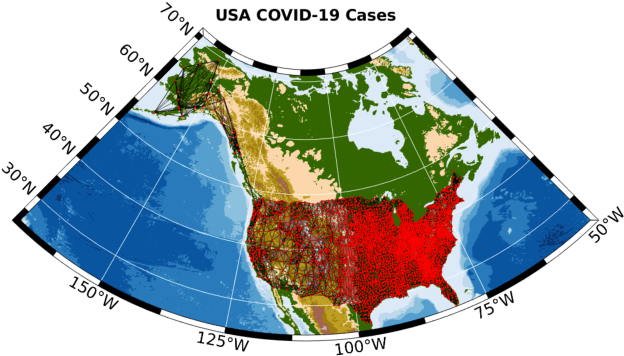
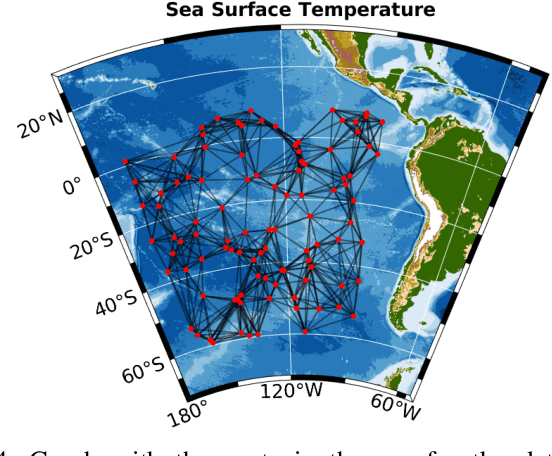
Abstract:Graph Signal Processing (GSP) is an emerging research field that extends the concepts of digital signal processing to graphs. GSP has numerous applications in different areas such as sensor networks, machine learning, and image processing. The sampling and reconstruction of static graph signals have played a central role in GSP. However, many real-world graph signals are inherently time-varying and the smoothness of the temporal differences of such graph signals may be used as a prior assumption. In the current work, we assume that the temporal differences of graph signals are smooth, and we introduce a novel algorithm based on the extension of a Sobolev smoothness function for the reconstruction of time-varying graph signals from discrete samples. We explore some theoretical aspects of the convergence rate of our Time-varying Graph signal Reconstruction via Sobolev Smoothness (GraphTRSS) algorithm by studying the condition number of the Hessian associated with our optimization problem. Our algorithm has the advantage of converging faster than other methods that are based on Laplacian operators without requiring expensive eigenvalue decomposition or matrix inversions. The proposed GraphTRSS is evaluated on several datasets including two COVID-19 datasets and it has outperformed many existing state-of-the-art methods for time-varying graph signal reconstruction. GraphTRSS has also shown excellent performance on two environmental datasets for the recovery of particulate matter and sea surface temperature signals.
Interpretable Stability Bounds for Spectral Graph Filters
Feb 18, 2021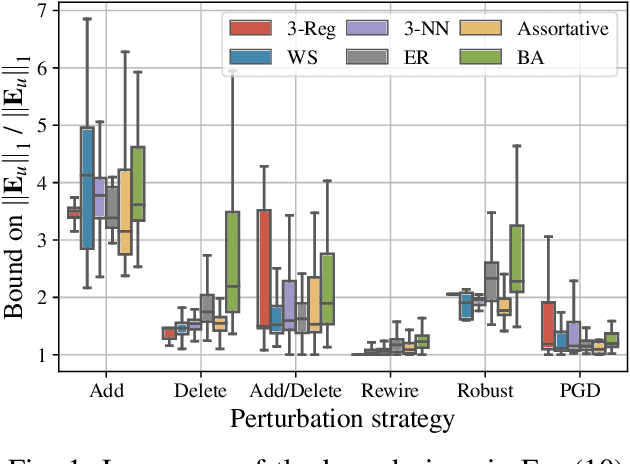
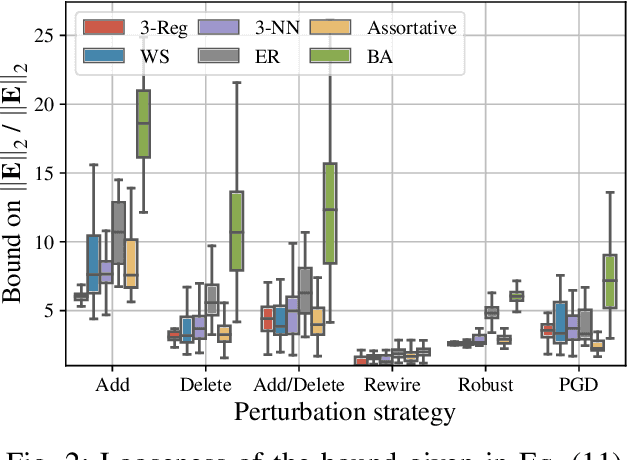
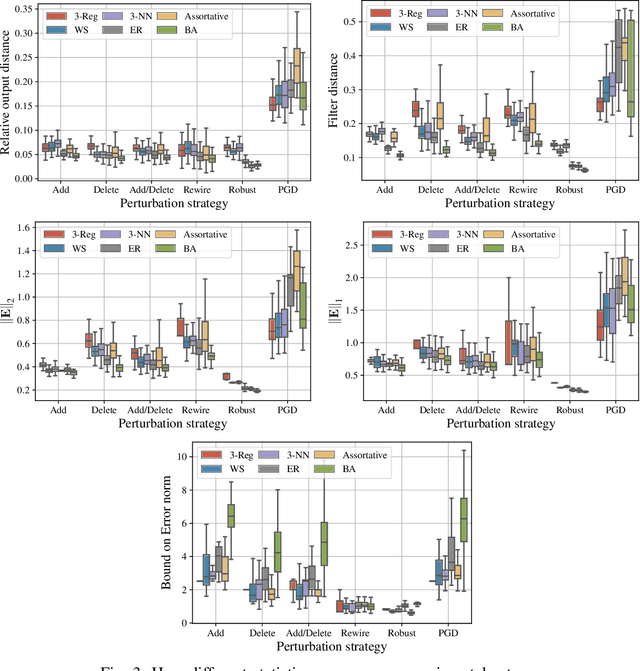
Abstract:Graph-structured data arise in a variety of real-world context ranging from sensor and transportation to biological and social networks. As a ubiquitous tool to process graph-structured data, spectral graph filters have been used to solve common tasks such as denoising and anomaly detection, as well as design deep learning architectures such as graph neural networks. Despite being an important tool, there is a lack of theoretical understanding of the stability properties of spectral graph filters, which are important for designing robust machine learning models. In this paper, we study filter stability and provide a novel and interpretable upper bound on the change of filter output, where the bound is expressed in terms of the endpoint degrees of the deleted and newly added edges, as well as the spatial proximity of those edges. This upper bound allows us to reason, in terms of structural properties of the graph, when a spectral graph filter will be stable. We further perform extensive experiments to verify intuition that can be gained from the bound.
On the Stability of Graph Convolutional Neural Networks under Edge Rewiring
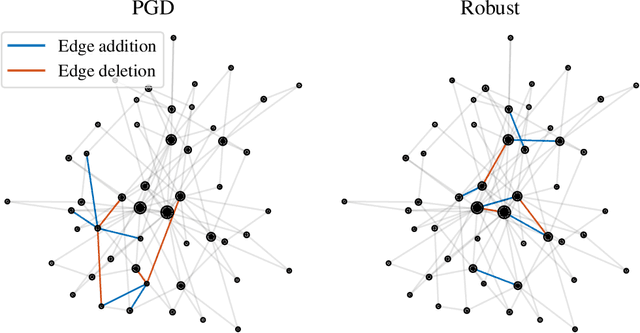
Oct 26, 2020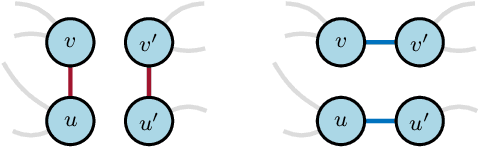
Abstract:Graph neural networks are experiencing a surge of popularity within the machine learning community due to their ability to adapt to non-Euclidean domains and instil inductive biases. Despite this, their stability, i.e., their robustness to small perturbations in the input, is not yet well understood. Although there exists some results showing the stability of graph neural networks, most take the form of an upper bound on the magnitude of change due to a perturbation in the graph topology. However, these existing bounds tend to be expressed in terms of uninterpretable variables, limiting our understanding of the model robustness properties. In this work, we develop an interpretable upper bound elucidating that graph neural networks are stable to rewiring between high degree nodes. This bound and further research in bounds of similar type provide further understanding of the stability properties of graph neural networks.
Graph signal processing for machine learning: A review and new perspectives
Jul 31, 2020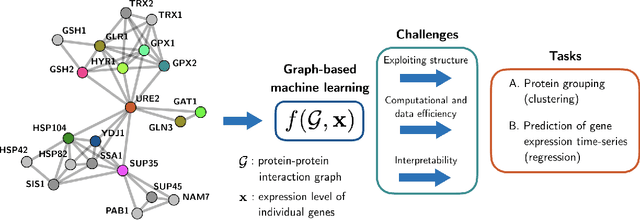
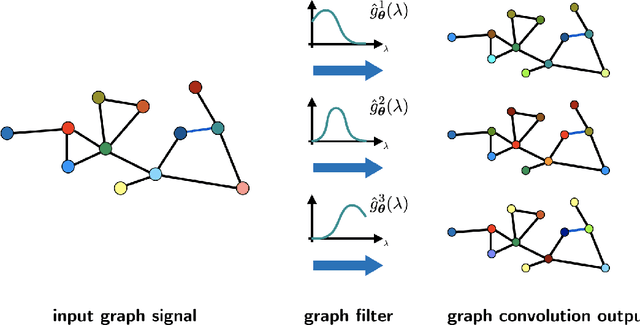
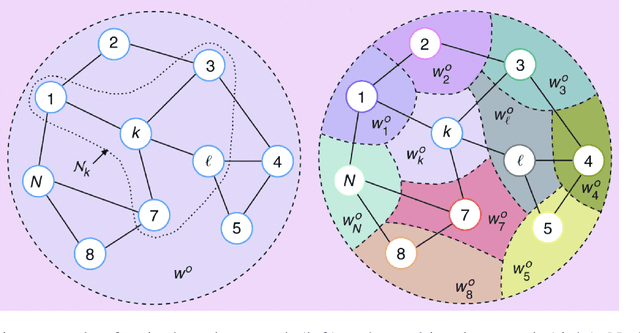
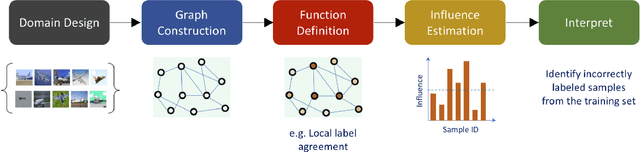
Abstract:The effective representation, processing, analysis, and visualization of large-scale structured data, especially those related to complex domains such as networks and graphs, are one of the key questions in modern machine learning. Graph signal processing (GSP), a vibrant branch of signal processing models and algorithms that aims at handling data supported on graphs, opens new paths of research to address this challenge. In this article, we review a few important contributions made by GSP concepts and tools, such as graph filters and transforms, to the development of novel machine learning algorithms. In particular, our discussion focuses on the following three aspects: exploiting data structure and relational priors, improving data and computational efficiency, and enhancing model interpretability. Furthermore, we provide new perspectives on future development of GSP techniques that may serve as a bridge between applied mathematics and signal processing on one side, and machine learning and network science on the other. Cross-fertilization across these different disciplines may help unlock the numerous challenges of complex data analysis in the modern age.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge