Higher-Order GNNs Meet Efficiency: Sparse Sobolev Graph Neural Networks

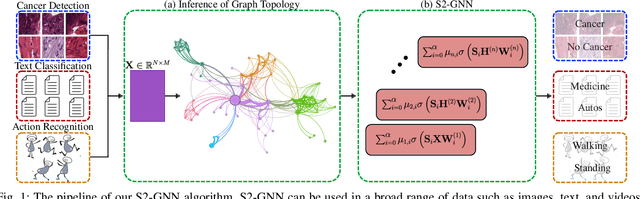
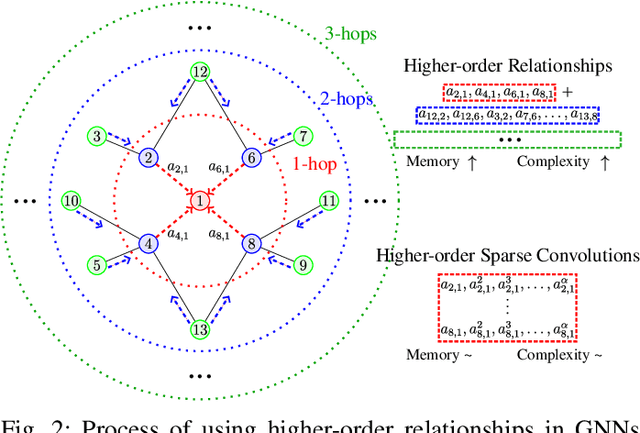
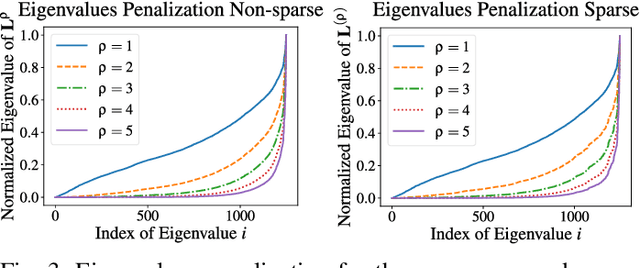
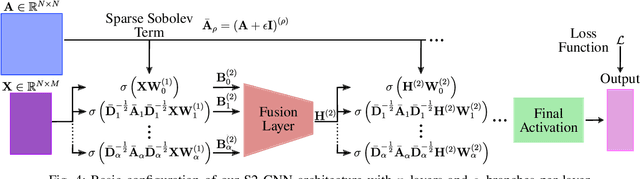
Graph Neural Networks (GNNs) have shown great promise in modeling relationships between nodes in a graph, but capturing higher-order relationships remains a challenge for large-scale networks. Previous studies have primarily attempted to utilize the information from higher-order neighbors in the graph, involving the incorporation of powers of the shift operator, such as the graph Laplacian or adjacency matrix. This approach comes with a trade-off in terms of increased computational and memory demands. Relying on graph spectral theory, we make a fundamental observation: the regular and the Hadamard power of the Laplacian matrix behave similarly in the spectrum. This observation has significant implications for capturing higher-order information in GNNs for various tasks such as node classification and semi-supervised learning. Consequently, we propose a novel graph convolutional operator based on the sparse Sobolev norm of graph signals. Our approach, known as Sparse Sobolev GNN (S2-GNN), employs Hadamard products between matrices to maintain the sparsity level in graph representations. S2-GNN utilizes a cascade of filters with increasing Hadamard powers to generate a diverse set of functions. We theoretically analyze the stability of S2-GNN to show the robustness of the model against possible graph perturbations. We also conduct a comprehensive evaluation of S2-GNN across various graph mining, semi-supervised node classification, and computer vision tasks. In particular use cases, our algorithm demonstrates competitive performance compared to state-of-the-art GNNs in terms of performance and running time.

Discovering Local Binary Pattern Equation for Foreground Object Removal in Videos

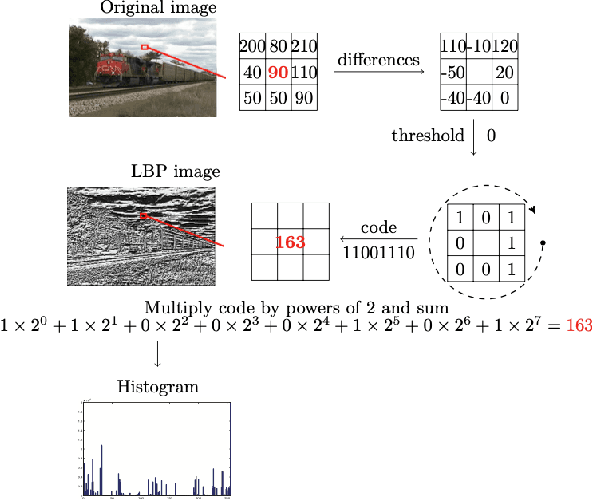
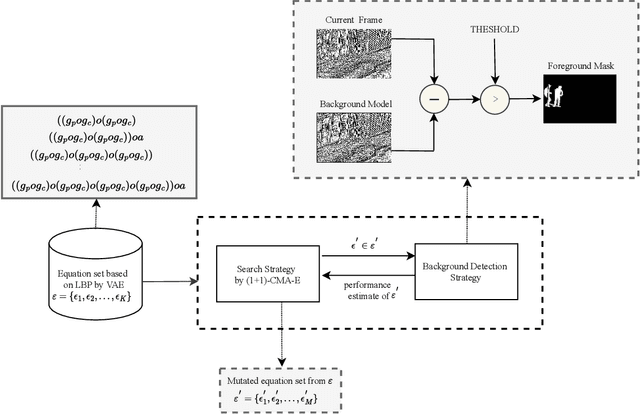
Designing a novel Local Binary Pattern (LBP) process usually relies heavily on human experts' knowledge and experience in the area. Even experts are often left with tedious episodes of trial and error until they identify an optimal LBP for a particular dataset. To address this problem, we present a novel symbolic regression able to automatically discover LBP formulas to remove the moving parts of a scene by segmenting it into a background and a foreground. Experimental results conducted on real videos of outdoor urban scenes under various conditions show that the LBPs discovered by the proposed approach significantly outperform the previous state-of-the-art LBP descriptors both qualitatively and quantitatively. Our source code and data will be available online.

Inductive Graph Neural Networks for Moving Object Segmentation

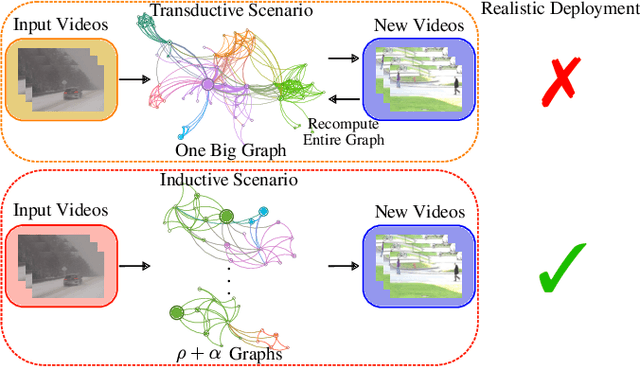
Moving Object Segmentation (MOS) is a challenging problem in computer vision, particularly in scenarios with dynamic backgrounds, abrupt lighting changes, shadows, camouflage, and moving cameras. While graph-based methods have shown promising results in MOS, they have mainly relied on transductive learning which assumes access to the entire training and testing data for evaluation. However, this assumption is not realistic in real-world applications where the system needs to handle new data during deployment. In this paper, we propose a novel Graph Inductive Moving Object Segmentation (GraphIMOS) algorithm based on a Graph Neural Network (GNN) architecture. Our approach builds a generic model capable of performing prediction on newly added data frames using the already trained model. GraphIMOS outperforms previous inductive learning methods and is more generic than previous transductive techniques. Our proposed algorithm enables the deployment of graph-based MOS models in real-world applications.

Time-varying Signals Recovery via Graph Neural Networks

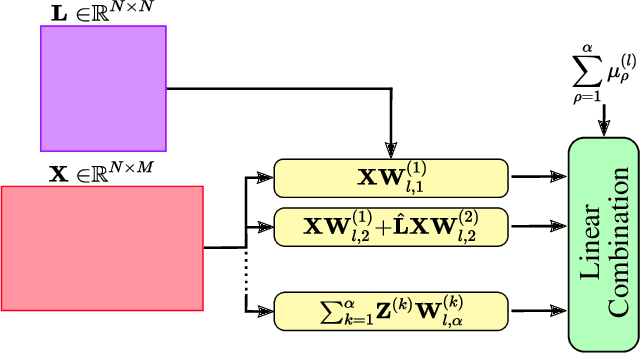
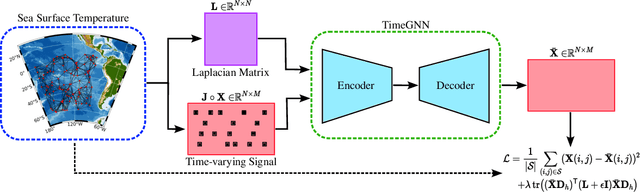
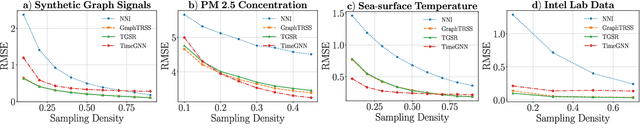
The recovery of time-varying graph signals is a fundamental problem with numerous applications in sensor networks and forecasting in time series. Effectively capturing the spatio-temporal information in these signals is essential for the downstream tasks. Previous studies have used the smoothness of the temporal differences of such graph signals as an initial assumption. Nevertheless, this smoothness assumption could result in a degradation of performance in the corresponding application when the prior does not hold. In this work, we relax the requirement of this hypothesis by including a learning module. We propose a Time Graph Neural Network (TimeGNN) for the recovery of time-varying graph signals. Our algorithm uses an encoder-decoder architecture with a specialized loss composed of a mean squared error function and a Sobolev smoothness operator.TimeGNN shows competitive performance against previous methods in real datasets.

Higher-order Sparse Convolutions in Graph Neural Networks

Graph Neural Networks (GNNs) have been applied to many problems in computer sciences. Capturing higher-order relationships between nodes is crucial to increase the expressive power of GNNs. However, existing methods to capture these relationships could be infeasible for large-scale graphs. In this work, we introduce a new higher-order sparse convolution based on the Sobolev norm of graph signals. Our Sparse Sobolev GNN (S-SobGNN) computes a cascade of filters on each layer with increasing Hadamard powers to get a more diverse set of functions, and then a linear combination layer weights the embeddings of each filter. We evaluate S-SobGNN in several applications of semi-supervised learning. S-SobGNN shows competitive performance in all applications as compared to several state-of-the-art methods.

Understanding the Relationship between Over-smoothing and Over-squashing in Graph Neural Networks

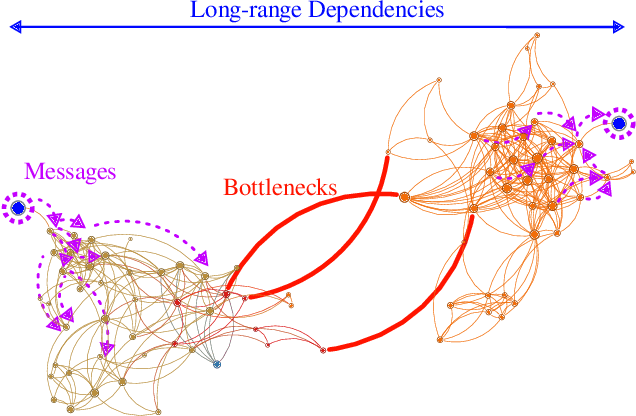
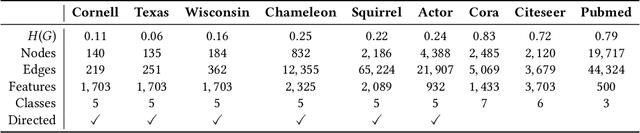
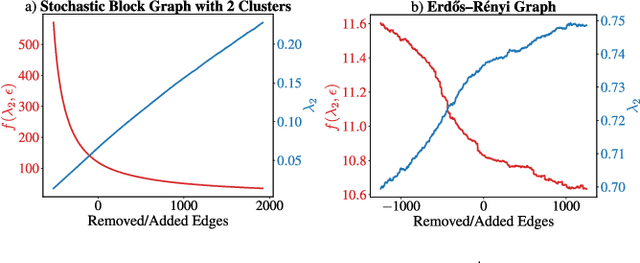
Graph Neural Networks (GNNs) have been successfully applied in many applications in computer sciences. Despite the success of deep learning architectures in other domains, deep GNNs still underperform their shallow counterparts. There are many open questions about deep GNNs, but over-smoothing and over-squashing are perhaps the most intriguing issues. When stacking multiple graph convolutional layers, the over-smoothing and over-squashing problems arise and have been defined as the inability of GNNs to learn deep representations and propagate information from distant nodes, respectively. Even though the widespread definitions of both problems are similar, these phenomena have been studied independently. This work strives to understand the underlying relationship between over-smoothing and over-squashing from a topological perspective. We show that both problems are intrinsically related to the spectral gap of the Laplacian of the graph. Therefore, there is a trade-off between these two problems, i.e., we cannot simultaneously alleviate both over-smoothing and over-squashing. We also propose a Stochastic Jost and Liu curvature Rewiring (SJLR) algorithm based on a bound of the Ollivier's Ricci curvature. SJLR is less expensive than previous curvature-based rewiring methods while retaining fundamental properties. Finally, we perform a thorough comparison of SJLR with previous techniques to alleviate over-smoothing or over-squashing, seeking to gain a better understanding of both problems.

Hypergraph Convolutional Networks for Weakly-Supervised Semantic Segmentation

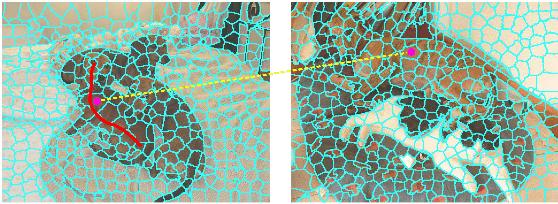
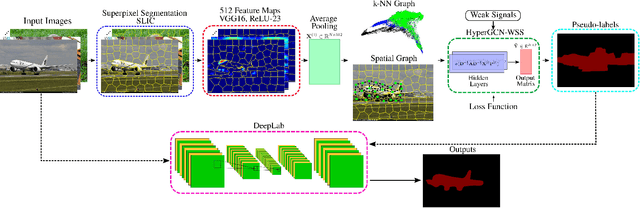
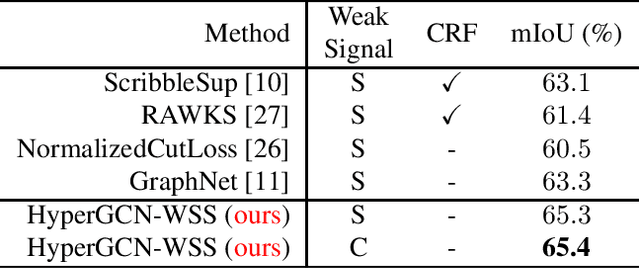
Semantic segmentation is a fundamental topic in computer vision. Several deep learning methods have been proposed for semantic segmentation with outstanding results. However, these models require a lot of densely annotated images. To address this problem, we propose a new algorithm that uses HyperGraph Convolutional Networks for Weakly-supervised Semantic Segmentation (HyperGCN-WSS). Our algorithm constructs spatial and k-Nearest Neighbor (k-NN) graphs from the images in the dataset to generate the hypergraphs. Then, we train a specialized HyperGraph Convolutional Network (HyperGCN) architecture using some weak signals. The outputs of the HyperGCN are denominated pseudo-labels, which are later used to train a DeepLab model for semantic segmentation. HyperGCN-WSS is evaluated on the PASCAL VOC 2012 dataset for semantic segmentation, using scribbles or clicks as weak signals. Our algorithm shows competitive performance against previous methods.

Graph CNN for Moving Object Detection in Complex Environments from Unseen Videos

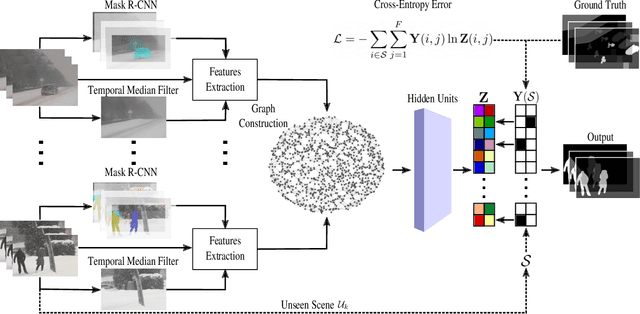
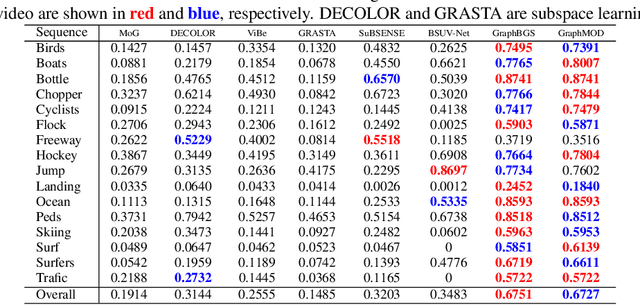
Moving Object Detection (MOD) is a fundamental step for many computer vision applications. MOD becomes very challenging when a video sequence captured from a static or moving camera suffers from the challenges: camouflage, shadow, dynamic backgrounds, and lighting variations, to name a few. Deep learning methods have been successfully applied to address MOD with competitive performance. However, in order to handle the overfitting problem, deep learning methods require a large amount of labeled data which is a laborious task as exhaustive annotations are always not available. Moreover, some MOD deep learning methods show performance degradation in the presence of unseen video sequences because the testing and training splits of the same sequences are involved during the network learning process. In this work, we pose the problem of MOD as a node classification problem using Graph Convolutional Neural Networks (GCNNs). Our algorithm, dubbed as GraphMOD-Net, encompasses instance segmentation, background initialization, feature extraction, and graph construction. GraphMOD-Net is tested on unseen videos and outperforms state-of-the-art methods in unsupervised, semi-supervised, and supervised learning in several challenges of the Change Detection 2014 (CDNet2014) and UCSD background subtraction datasets.

Reconstruction of Time-varying Graph Signals via Sobolev Smoothness

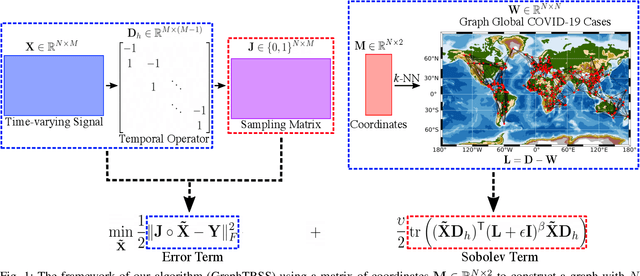
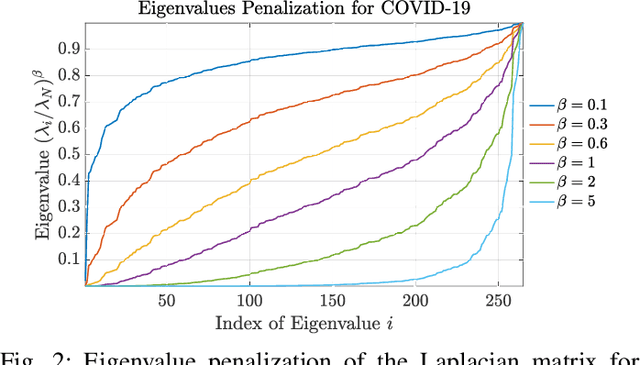
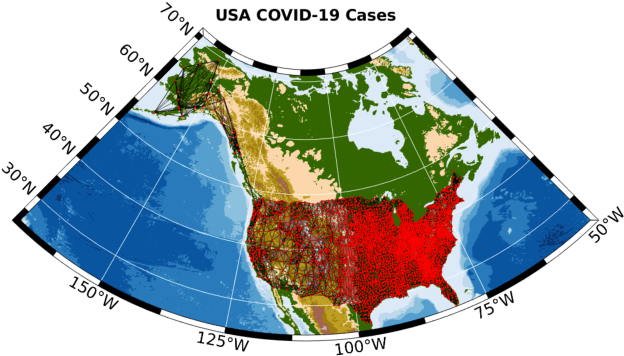
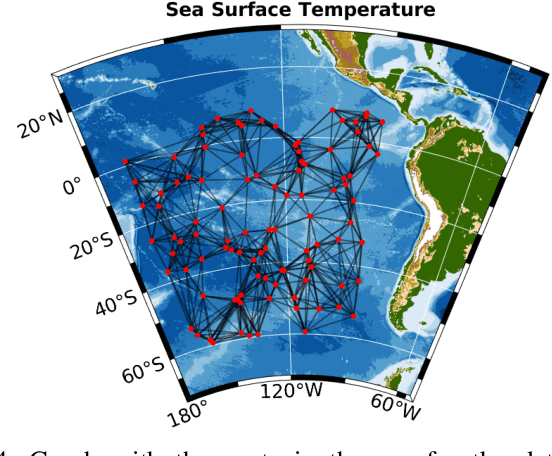
Graph Signal Processing (GSP) is an emerging research field that extends the concepts of digital signal processing to graphs. GSP has numerous applications in different areas such as sensor networks, machine learning, and image processing. The sampling and reconstruction of static graph signals have played a central role in GSP. However, many real-world graph signals are inherently time-varying and the smoothness of the temporal differences of such graph signals may be used as a prior assumption. In the current work, we assume that the temporal differences of graph signals are smooth, and we introduce a novel algorithm based on the extension of a Sobolev smoothness function for the reconstruction of time-varying graph signals from discrete samples. We explore some theoretical aspects of the convergence rate of our Time-varying Graph signal Reconstruction via Sobolev Smoothness (GraphTRSS) algorithm by studying the condition number of the Hessian associated with our optimization problem. Our algorithm has the advantage of converging faster than other methods that are based on Laplacian operators without requiring expensive eigenvalue decomposition or matrix inversions. The proposed GraphTRSS is evaluated on several datasets including two COVID-19 datasets and it has outperformed many existing state-of-the-art methods for time-varying graph signal reconstruction. GraphTRSS has also shown excellent performance on two environmental datasets for the recovery of particulate matter and sea surface temperature signals.

Moving Object Detection for Event-based vision using Graph Spectral Clustering

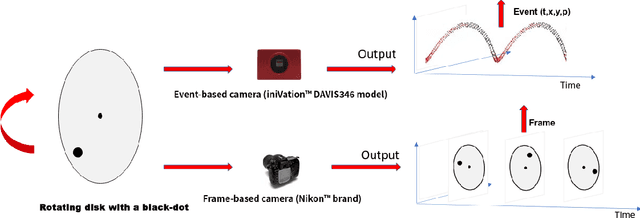
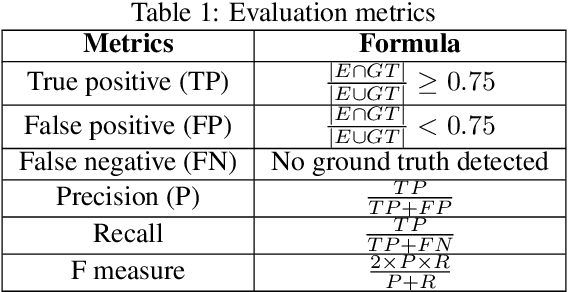
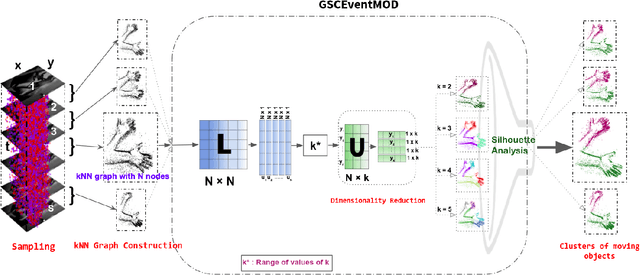
Moving object detection has been a central topic of discussion in computer vision for its wide range of applications like in self-driving cars, video surveillance, security, and enforcement. Neuromorphic Vision Sensors (NVS) are bio-inspired sensors that mimic the working of the human eye. Unlike conventional frame-based cameras, these sensors capture a stream of asynchronous 'events' that pose multiple advantages over the former, like high dynamic range, low latency, low power consumption, and reduced motion blur. However, these advantages come at a high cost, as the event camera data typically contains more noise and has low resolution. Moreover, as event-based cameras can only capture the relative changes in brightness of a scene, event data do not contain usual visual information (like texture and color) as available in video data from normal cameras. So, moving object detection in event-based cameras becomes an extremely challenging task. In this paper, we present an unsupervised Graph Spectral Clustering technique for Moving Object Detection in Event-based data (GSCEventMOD). We additionally show how the optimum number of moving objects can be automatically determined. Experimental comparisons on publicly available datasets show that the proposed GSCEventMOD algorithm outperforms a number of state-of-the-art techniques by a maximum margin of 30%.