Higher-Order GNNs Meet Efficiency: Sparse Sobolev Graph Neural Networks

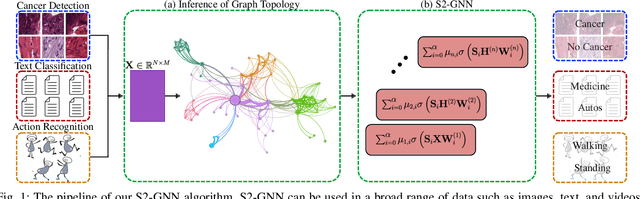
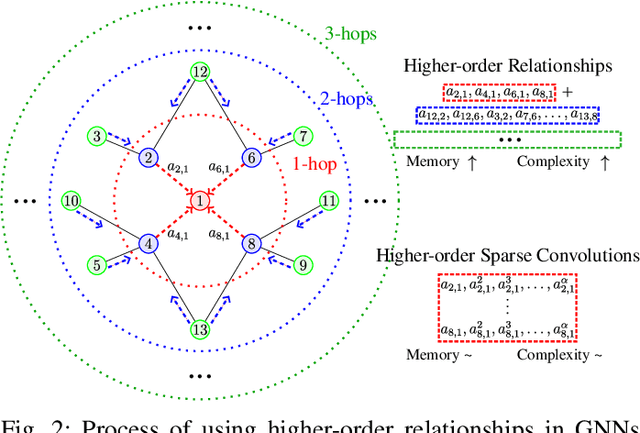
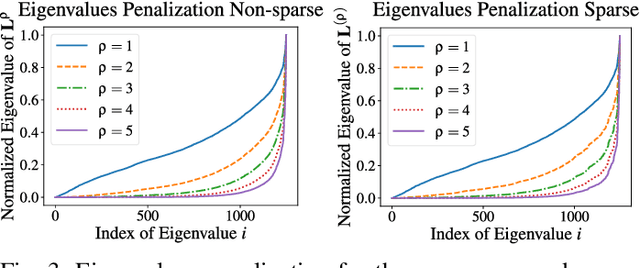
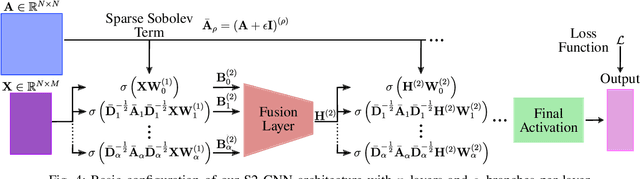
Graph Neural Networks (GNNs) have shown great promise in modeling relationships between nodes in a graph, but capturing higher-order relationships remains a challenge for large-scale networks. Previous studies have primarily attempted to utilize the information from higher-order neighbors in the graph, involving the incorporation of powers of the shift operator, such as the graph Laplacian or adjacency matrix. This approach comes with a trade-off in terms of increased computational and memory demands. Relying on graph spectral theory, we make a fundamental observation: the regular and the Hadamard power of the Laplacian matrix behave similarly in the spectrum. This observation has significant implications for capturing higher-order information in GNNs for various tasks such as node classification and semi-supervised learning. Consequently, we propose a novel graph convolutional operator based on the sparse Sobolev norm of graph signals. Our approach, known as Sparse Sobolev GNN (S2-GNN), employs Hadamard products between matrices to maintain the sparsity level in graph representations. S2-GNN utilizes a cascade of filters with increasing Hadamard powers to generate a diverse set of functions. We theoretically analyze the stability of S2-GNN to show the robustness of the model against possible graph perturbations. We also conduct a comprehensive evaluation of S2-GNN across various graph mining, semi-supervised node classification, and computer vision tasks. In particular use cases, our algorithm demonstrates competitive performance compared to state-of-the-art GNNs in terms of performance and running time.

Gegenbauer Graph Neural Networks for Time-varying Signal Reconstruction

Reconstructing time-varying graph signals (or graph time-series imputation) is a critical problem in machine learning and signal processing with broad applications, ranging from missing data imputation in sensor networks to time-series forecasting. Accurately capturing the spatio-temporal information inherent in these signals is crucial for effectively addressing these tasks. However, existing approaches relying on smoothness assumptions of temporal differences and simple convex optimization techniques have inherent limitations. To address these challenges, we propose a novel approach that incorporates a learning module to enhance the accuracy of the downstream task. To this end, we introduce the Gegenbauer-based graph convolutional (GegenConv) operator, which is a generalization of the conventional Chebyshev graph convolution by leveraging the theory of Gegenbauer polynomials. By deviating from traditional convex problems, we expand the complexity of the model and offer a more accurate solution for recovering time-varying graph signals. Building upon GegenConv, we design the Gegenbauer-based time Graph Neural Network (GegenGNN) architecture, which adopts an encoder-decoder structure. Likewise, our approach also utilizes a dedicated loss function that incorporates a mean squared error component alongside Sobolev smoothness regularization. This combination enables GegenGNN to capture both the fidelity to ground truth and the underlying smoothness properties of the signals, enhancing the reconstruction performance. We conduct extensive experiments on real datasets to evaluate the effectiveness of our proposed approach. The experimental results demonstrate that GegenGNN outperforms state-of-the-art methods, showcasing its superior capability in recovering time-varying graph signals.

Time-varying Signals Recovery via Graph Neural Networks

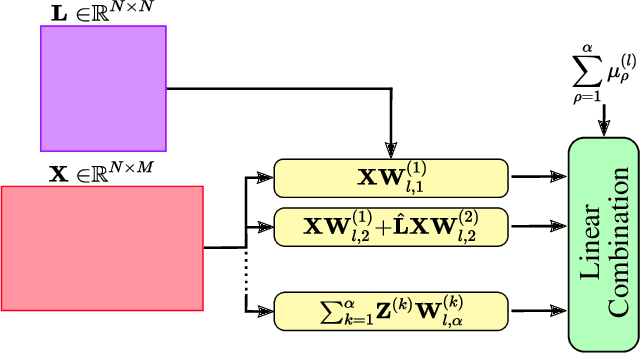
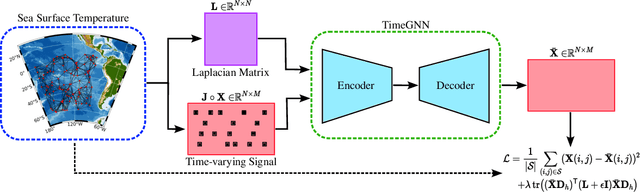
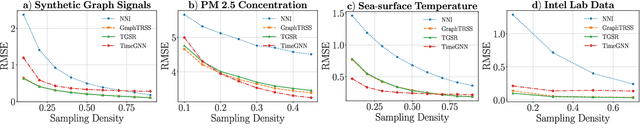
The recovery of time-varying graph signals is a fundamental problem with numerous applications in sensor networks and forecasting in time series. Effectively capturing the spatio-temporal information in these signals is essential for the downstream tasks. Previous studies have used the smoothness of the temporal differences of such graph signals as an initial assumption. Nevertheless, this smoothness assumption could result in a degradation of performance in the corresponding application when the prior does not hold. In this work, we relax the requirement of this hypothesis by including a learning module. We propose a Time Graph Neural Network (TimeGNN) for the recovery of time-varying graph signals. Our algorithm uses an encoder-decoder architecture with a specialized loss composed of a mean squared error function and a Sobolev smoothness operator.TimeGNN shows competitive performance against previous methods in real datasets.